 Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
15. Αναγωγή στη δεκαδική κλασματική μονάδα
Σ’ αυτό το κεφάλαιο θα μάθουμε:
- Πώς βρίσκουμε το μέρος μιας ποσότητας, όταν γνωρίζουμε ολόκληρη την ποσότητα;
- Πώς βρίσκουμε ολόκληρη την ποσότητα, αν γνωρίζουμε ένα μέρος της;
Μερικές φορές όταν ακούμε για πρώτη φορά κάτι μας φαίνεται δύσκολο και περίπλοκο. Έτσι μπορεί να νομίζεται κι αυτή τη στιγμή! Όμως, συνήθως ότι στην αρχή μας φαίνεται ακαταλαβίστικο και πολύπλοκο, στη συνέχεια, αν το ξαναδιαβάσουμε με περισσότερη προσοχή, βλέπουμε ότι είναι πανεύκολο!
Θυμάμαι!

![]()
Αν γνωρίζω το δεκαδικό μέρος μιας ποσότητας και θέλω να βρω όλη την ποσότητα ή ένα άλλο δεκαδικό μέρος της, μπορώ να κάνω αναγωγή στη δεκαδική κλασματική μονάδα. Παράδειγμα: Αν τα ![]() μιας ποσότητας είναι 32, πόσο είναι τα 9/10 της ίδιας ποσότητας; Αφού τα
μιας ποσότητας είναι 32, πόσο είναι τα 9/10 της ίδιας ποσότητας; Αφού τα ![]() είναι 32, τότε το είναι 32 : 4 = 8. Άρα
είναι 32, τότε το είναι 32 : 4 = 8. Άρα ![]() είναι 9 x 8 = 72.
είναι 9 x 8 = 72.
Δείτε την παρουσίαση του μαθήματος
(δημιουργός Αργυρώ Μάνθου)
[slideboom id=1342686&w=425&h=370]
Ώρα για εξάσκηση
- Η Βιβιάννα πρόσφερε στη φίλη της, τη Χρύσα μια ανθοδέσμη με 20 τριαντάφυλλα για τη γιορτή της. Από αυτά τα 7/10 ήταν κόκκινα και τα υπόλοιπα λευκά. Πόσα ήταν τα κόκκινα και πόσα τα λευκά τριαντάφυλλα;
- Αγόρασα με τα 3/10 των χρημάτων μου 2 βιβλία λογοτεχνίας. Αν το κάθε βιβλίο έκανε 15 ευρώ, πόσα χρήματα είχα αρχικά;
- Τα 8/10 του βάρους ενός φορτίου είναι 56 κιλά.Πόσο ζυγίζει όλο το φορτίο;
- Ο κ. Νίκος περπατάει κάθε μέρα 4 χμ. Σήμερα περπάτησε επιπλέον τα 2/10 της καθημερινής του διαδρομής. Πόσα μέτρα περπάτησε σήμερα;
_________________________________________________________________________________________________________________________________________
 Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
16. Κλασματικές μονάδες

![]()
Η κλασματική μονάδα είναι ένας αριθμός που μας δείχνει σε πόσα ίσα μέρη έχει χωριστεί μια ποσότητα.
Παράδειγμα: ![]() του
του ![]() σημαίνει ότι το εξάγωνο
σημαίνει ότι το εξάγωνο ![]() έχει χωριστεί σε 6 ίσα μέρη.
έχει χωριστεί σε 6 ίσα μέρη.
Ανάμεσα σε δύο ή περισσότερες κλασματικές μονάδες που αναφέρονται στην ίδια ποσότητα, μεγαλύτερη είναι αυτή που έχει το μικρότερο παρονομαστή.
Παράδειγμα: ![]()
Δείτε την παρουσίαση του μαθήματος
[slideboom id=425990&w=425&h=370]
Δείτε
Ώρα για εξάσκηση
Πάτησε στην εικόνα, διάλεξε επίπεδο (level) και εξασκήσου με τις κλασματικές πίτσες!!!
_________________________________________________________________________________________________________________________________________
 Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
17. Ισοδύναμα κλάσματα
- Ποια κλάσματα λέμε ισοδύναμα
Δύο ή περισσότερα κλάσματα λέγονται ισοδύναμα ή ίσα όταν έχουν την ίδια αξία αλλά διαφορετικούς όρους .
- Πώς μπορούμε να φτιάξουμε ισοδύναμα κλάσματα
Ισοδύναμα κλάσματα μπορούμε να φτιάξουμε αν πολλαπλασιάσουμε τους όρους του κλάσματος [αριθμητή και παρονομαστή] με τον ίδιο αριθμό ή αν τους διαιρέσουμε με τον ίδιο αριθμό.

- Τι λέμε “απλοποίηση“
Όταν διαιρώ τους όρους του κλάσματος με τον ίδιο αριθμό και φτιάχνω ισοδύναμα κλάσματα με μικρότερους όρους τότε κάνω απλοποίηση
- Ποια κλάσματα λέμε “ανάγωγα“
Τα κλάσματα που δεν απλοποπιούνται άλλο λέγονται ανάγωγα
- Ποια κλάσματα λέγονται “ομώνυμα“
Τα κλάσματα που έχουν ίδιους παρονομαστές λέγονται ομώνυμα
- Ποια κλάσματα λέγονται “ετερώνυμα“
Τα κλάσματα που έχουν διαφορετικούς παρονομαστές λέγονται ετερώνυμα
Δείτε την παρουσίαση του μαθήματος
[slideboom id=459493&w=425&h=370]
[slideboom id=441008&w=425&h=370]
Ώρα για εξάσκηση!

 Φτιάχνω ισοδύναμα κλάσματα! [κλικ]
Φτιάχνω ισοδύναμα κλάσματα! [κλικ]

Βάλε τα ισοδύναμα κλάσματα στο σωστό κύκλο! [κλικ]
_________________________________________________________________________________________________________________________________________
 Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
18. Μετατροπή κλάσματος σε δεκαδικό
Έχουμε μάθει ότι κάθε κλάσμα φανερώνει το ακριβές πηλίκο της διαίρεσης του αριθμητή με τον παρονομαστή.
![]()

![]() Όταν ο διαιρέτης είναι μεγαλύτερος από το διαιρετέο, τότε σίγουρα το πηλίκο είναι δεκαδικός αριθμός.
Όταν ο διαιρέτης είναι μεγαλύτερος από το διαιρετέο, τότε σίγουρα το πηλίκο είναι δεκαδικός αριθμός.
Δείτε την παρουσίαση του μαθήματος
[slideboom id=462919&w=425&h=370]
[slideboom id=463708&w=425&h=370]
Ώρα για εξάσκηση!
[κλικ στην εικόνα]
_________________________________________________________________________________________________________________________________________
Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
27. Πολλαπλασιασμός κλασμάτων – Αντίστροφοι αριθμοί
Για να πολλαπλασιάσουμε δύο κλάσματα, σχηματίζουμε ένα νέο κλάσμα που έχει στον αριθμητή το γινόμενο των αριθμητών και στον παρονομαστή το γινόμενο των παρονομαστών.
Πρέπει να θυμόμαστε ότι:
για να πολλαπλασιάσω δυο κλάσματα ακολουθώ την παρακάτω διαδρομή:
1. Πολλαπλασιάζω αριθμητές
2. Πολλαπλασιάζω παρονομαστές
3. Απλοποιώ το τελικό κλάσμα (αν χρειάζεται)
- με οποιαδήποτε σειρά κι αν πολλαπλασιάσουμε δύο κλάσματα το αποτέλεσμα είναι το ίδιο.

Κι αν έχω να πολλαπλασιάσω κλάσμα με ακέραιο;
- Κάθε ακέραιος μπορεί να γραφτεί ως κλάσμα με παρονομαστή τη μονάδα.

μετά συνεχίζω όπως έμαθα τον πολλαπλασιασμό των κλασμάτων

ή
Αν θέλουμε να πολλαπλασιάσουμε ακέραιο αριθμό με κλάσμα, πολλαπλασιάζουμε τον ακέραιο μόνο με τον αριθμητή του κλάσματος…

Αν θέλουμε να πολλαπλασιάσουμε μεικτό αριθμό με κλάσμα, μπορούμε να μετατρέψουμε το μεικτό αριθμό σε κλάσμα και στη συνέχεια να κάνουμε πολλαπλασιασμό κλασμάτων.
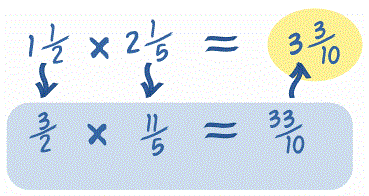
Κι αν έχω να πολλαπλασιάσω κλάσμα με δεκαδικό;
Αν θέλουμε να πολλαπλασιάσουμε δεκαδικό αριθμό με κλάσμα, μπορούμε να μετατρέψουμε το δεκαδικό αριθμό σε δεκαδικό κλάσμα και στη συνέχεια να κάνουμε πολλαπλασιασμό κλασμάτων.




Δείτε την παρουσίαση του μαθήματος
[slideboom id=483217&w=425&h=370]
Ώρα για εξάσκηση!
κλικ στην παρακάτω εικόνα
_________________________________________________________________________________________________________________________________________
 Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
28. Διαίρεση μέτρησης σε ομώνυμα κλάσματα
Με μια διαίρεση μέτρησης βρίσκω πόσες φορές “χωράει” μια μικρότερη ποσότητα σε μια μεγαλύτερη.
-
τα κάνω πρώτα ομώνυμα (αν δεν είναι)
-
διαιρώ τους αριθμητές τους
Φάτε μόνο τη μισή. Υπάρχει λόγος…
Τώρα έχετε περίσσευμα το 1/2 της σοκολάτας.
Σύμφωνα με τις τελευταίες έρευνες η κατανάλωση ενός μικρού κομματιού σοκολάτας καθημερινά είναι ωφέλιμη.
Πόσο μικρό να είναι άραγε το κομματάκι; Γύρω στο 1/8 της σοκολάτας είναι καλά…
Άραγε για πόσες μέρες θα φτάσει το 1/2 της σοκολάτας αν τρώτε κάθε μέρα από 1/8 της ίδιας σοκολάτας;
Σαν να μου φαίνεται ότι έχετε μπροστά σας μια δύσκολη διαίρεση… 1/2:1/8.
Με την ενέργεια που πήρατε από την κατανάλωση σοκολάτας που προηγήθηκε, σκέφτεστε το εξής:
“Μήπως μπορώ να εκφράσω το 1/2 της σοκολάτας σε όγδοα;”
Αν όλη η σοκολάτα είναι 8/8, η μισή θα είναι 4/8, εύκολο αυτό.
Τώρα τα πράγματα έγιναν πιο απλά : έχετε να διαιρέσετε τα 4/8 με το 1/8.
Το 1/8 χωρά στο 4/8 τόσες φορές, όσες χωρά το 1 στο 4. Δηλαδή έχετε σοκολάτα για 4 μέρες.
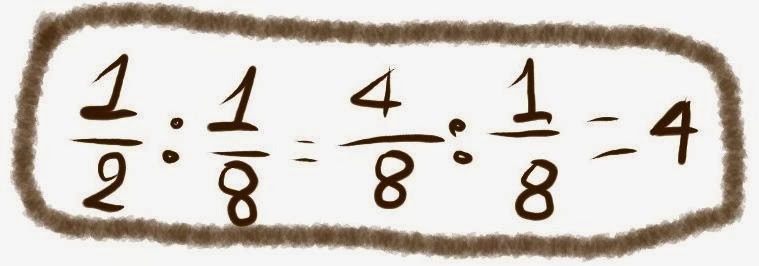 το είδα στο : http://meta-sxoleio.blogspot.gr/2014/01/diairesi-metrisis-se-omonyma-klasmata.html… και μου άρεσε!
το είδα στο : http://meta-sxoleio.blogspot.gr/2014/01/diairesi-metrisis-se-omonyma-klasmata.html… και μου άρεσε!29. Σύνθετα προβλήματα – Επαλήθευση
![]()
Όταν λύνουμε ένα πρόβλημα, στο τέλος ελέγχουμε πάντα τη λύση που δώσαμε:
- Χρησιμοποιώντας μια άλλη στρατηγική.
- Συγκρίνοντας το τελικό αποτέλεσμα με την αρχική μας εκτίμηση.
Ώρα για εξάσκηση!
Προβλήματα
1. Ο ιδιοκτήτης ενός καταστήματος ηλεκτρικών ειδών πούλησε το Ιανουάριο 12 ψυγεία και τον Μάρτιο 9. Αν η τιμή πώλησης κάθε ψυγείου ήταν 815 ευρώ, πόσα χρήματα εισέπραξε συνολικά ο καταστηματάρχης;
2. Η κυρία Μαίρη έφτιαξε 4,6 κιλά μαρμελάδα ροδάκινο και θέλει να τη βάλει σε βαζάκια. Αν το κάθε βαζάκι χωράει 2/10 του κιλού μαρμελάδα, πόσα βαζάκια θα χρειαστεί η κυρία Μαίρη;
3. Ο κ. Στέλιος θέλει να φτιάξει μια βιβλιοθήκη με 4 ράφια. Υπολόγισε ότι τα ράφια θα έχουν μήκος 75 εκ. Πόσες σανίδες των 1,50 μ. πρέπει να αγοράσει, ώστε να φτιάξει τα ράφια που θέλει;
4. Η Χριστίνα για να πάει στο σχολείο περπατάει 584 μέτρα. Στα 3/4 της απόστασης είναι το σπίτι της φίλης της Γεωργίας. Ποια είναι η απόσταση από το σπίτι της Γεωργίας μέχρι το σχολείο;
5. Η απόσταση Λάρισα- Φλώρινα είναι 231 χμ. Ο κ. Μανταλάκης – έμπορος από τους λίγους – έχει διανύσει τα 4/6 της διαδρομής. Πόσα χιλιόμετρα έχει διανύσει και πόσα του μένουν ακόμα για να φτάσει στον προορισμό του;
6. Ο παππούς του Αλέξανδρου έχει 32 κιλά κρασί και θέλει να το βάλει σε μπουκάλια. Αν το κάθε μπουκάλι χωράει 2/5 του κιλού, πόσα μπουκάλια θα γεμίσει;
7. Η Χρύσα μάζεψε από το χαρτζιλίκι της τα 4/5 των 2/3 των 60 ευρώ. Η Ναταλία μάζεψε το 1/4 των 3/6 των 200 ευρώ. Ποιο παιδί μάζεψε τα περισσότερα χρήματα;
_________________________________________________________________________________________________________________________________________
 Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
34. Διαίρεση ακεραίου και κλάσματος με κλάσμα κλάσματος με ακέραιο
![]()
Για να διαιρέσουμε έναν ακέραιο αριθμό με ένα κλάσμα ή ένα κλάσμα με ένα άλλο κλάσμα ή ένα κλάσμα με έναν ακέραιο, μπορούμε να αντιστρέψουμε τους όρους του διαιρέτη (κλάσμα ή ακέραιος) και αντί για διαίρεση να κάνουμε πολλαπλασιασμό.
Παραδείγματα:

Δείτε την παρουσίαση του μαθήματος
[slideboom id=485903&w=425&h=370]
Ώρα για εξάσκηση!
Πόσες διαιρέσεις μπορείς να κάνεις σε ένα λεπτό;
κλικ στην παρακάτω εικόνα
1. 2/3 : 5 =
0,8 : 1/6 =
4: 1 1/3 =
6/10 : 0,2 =
6/30 : 1/8 =
9/15 : 2 =
2. 3/8 : 1 6/10 =
3/9 : 1 8/12 =
18/5 : 0,2 =
32/15 : 5 =
0,4 : 2 1/16 =
3 1/4 : 5/10 =
3. 0,002 : 2/8 =
4,10 : 6/4 =
6/9 : 0,10 =
1 1/25 : 3/10 =
4 3/8 : 3/8 =
_________________________________________________________________________________________________________________________________________
 Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
Κάνε κλικ στην εικόνα για να διαβάσεις το μάθημα στο βιβλίο του μαθητή
39. Πρόσθεση και αφαίρεση ετερώνυμων κλασμάτων
![]()
Για να συγκρίνω, να προσθέσω ή να αφαιρέσω ετερώνυμα κλάσματα, τα μετατρέπω σε ομώνυμα, δηλαδή σε ισοδύναμα κλάσματα με κοινό παρονομαστή. O παρονομαστής των ομώνυμων κλασμάτων μπορεί να είναι οποιοδήποτε κοινό πολλαπλάσιο των παρονομαστών των αρχικών κλασμάτων ή άλλων που είναι ισοδύναμά τους. Αν χρησιμοποιήσω το Ε.Κ.Π. των παρονομαστών, θα έχω τα ομώνυμα κλάσματα με τους πιο μικρούς όρους.
Δείτε την παρουσίαση του μαθήματος
[slideboom id=478243&w=425&h=370]
[slideboom id=862474&w=425&h=370]
Δείτε
Ώρα για εξάσκηση!
Κάνουμε τις προσθέσεις των παρακάτω κλασμάτων.
1 + 2 + 2 =
4 5 10 Ε.Κ.Π.(4, 5, 10)=______________
2 + 3 + 3 =
6 8 12 Ε.Κ.Π.(6, 8, 12)=______________
3 + 5 + 13 =
12 15 30 Ε.Κ.Π.(12, 15, 30)=_____________
3 + 2 + 12 =
15 25 30 Ε.Κ.Π.(15, 25, 30)=_____________
1 + 2 + 2 =
2 15 25 Ε.Κ.Π.(2, 15, 25)=______________
4 + 2 + 3 =
8 9 12 Ε.Κ.Π.(8, 9, 12)=______________
Κάνουμε τις αφαιρέσεις των παρακάτω κλασμάτων.
3 – 4 =
4 9 Ε.Κ.Π.(4, 9)=________________
5 – 6 =
8 12 Ε.Κ.Π.(8, 12)=_______________
1 – 3 =
2 9 Ε.Κ.Π.(2, 9)=________________
5 – 10 =
6 15 Ε.Κ.Π.(6, 15)=_______________
8 – 7 =
10 12 Ε.Κ.Π.(10, 12)=______________









