Επανάληψη στους δεκαδικούς αριθμούς

Κάνε κλικ στην παρακάτω εικόνα για να θυμηθείς ό,τι μάθαμε στην Τετάρτη τάξη για τους δεκαδικούς αριθμούς.

Θυμόμαστε τους δεκαδικούς αριθμούς

Δείτε το στο slideshare.net

________________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

7. Δεκαδικοί αριθμοί – Δεκαδικά κλάσματα

Μπορούμε να φτιάξουμε την ακέραιη μονάδα με 10 δέκατα (10 x ή 10 x 0,10) ή με 100 εκατοστά (100 x ή 100 x 0,01).

Παράδειγμα: 1 =10 x 10 λ. ή 10 x 0,10

[slideboom id=427904&w=425&h=370]

Ώρα για εξάσκηση!

Πάτησε στην παρακάτω εικόνα

Επίλεξε το πρώτο ή το δεύτερο επίπεδο (Level one, level two).
Επίλεξε SLOW FRUIT για να κινούνται αργά τα φρούτα.
Με το ποντίκι μετακινείς το φρούτο και με αριστερό κλικ πυροβολείς το φρούτο που έχει τον αντίστοιχο δεκαδικό αριθμό με το κλάσμα που φαίνεται πάνω στο ποντίκι σου.

_______________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

8. Δεκαδικά κλάσματα – δεκαδικοί αριθμοί

Δεκαδικό κλάσμα ονομάζουμε το κλάσμα που έχει παρονομαστή το 10, το 100, το 1000 κτλ.

π.χ. 7/10, 25/100, 540/1000

Κάθε δεκαδικό κλάσμα μπορεί να γραφτεί και ως δεκαδικός αριθμός.

Οι δεκαδικοί αριθμοί αποτελούνται από δύο μέρη: το ακέραιο και το δεκαδικό μέρος. Το ακέραιο με το δεκαδικό μέρος χωρίζονται μεταξύ τους από την υποδιαστολή (,)

Χρησιμοποιούμε τους δεκαδικούς αριθμούς και τα δεκαδικά κλάσματα για να μετρήσουμε με ακρίβεια.

Παραδείγματα:

1 λίτρο αμόλυβδης βενζίνης κοστίζει 0,964.
Η δοσολογία που πρότεινε ο γιατρός είναι: 2 κουταλάκια σιρόπι ή 2/100 του λίτρου.

Δεκαδικά κλάσματα – Δεκαδικοί αριθμοί (μετράμε με ακρίβεια)

[slideboom id=432747&w=425&h=370]

Δεκαδικά κλάσματα – Δεκαδικοί αριθμοί (μετράμε με ακρίβεια)

(δημιουργός Γ. Σουδίας)

[slideboom id=432342&w=425&h=370]

_______________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

9. Αξία θέσης ψηφίων στους δεκαδικούς αριθμούς

Όταν συγκρίνουμε αριθμούς με δεκαδικά ψηφία, ξεκινάμε να συγκρίνουμε τα ψηφία που βρίσκονται από αριστερά, στις ακριβώς αντίστοιχες θέσεις. Παράδειγμα: • 9,850 κιλά > 9,225 κιλά, γιατί 9 = 9 και 8 > 2.

[slideboom id=430474&w=425&h=370]

Δημιουργός Π. Κώτσης

_______________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

11. Η έννοια της στρογγυλοποίησης

α. Πότε κάνουμε στρογγυλοποίηση

β. Πότε ΔΕΝ κάνουμε στρογγυλοποίηση

γ. Πώς κάνουμε στρογγυλοποίηση (τεχνικές)

δ. Παραδείγματα στρογγυλοποίησης σε φυσικούς και σε δεκαδικούς αριθμούς.

Στην καθημερινή μας ζωή δεν είναι πάντα απαραίτητο να κάνουμε υπολογισμούς με ακρίβεια. Υπάρχουν περιπτώσεις που η στρογγυλοποίηση των αριθμών μάς βοηθάει να εκτιμήσουμε γρήγορα ένα αποτέλεσμα. Συνήθως η διαφορά ανάμεσα στον ακριβή υπολογισμό και στην εκτίμηση (σφάλμα) δεν είναι σημαντική.

Παράδειγμα: 1 λίτρο βενζίνη: 0,999 € . Tο 1 λίτρο κοστίζει ουσιαστικά 1 €.
Πόσο κοστίζουν 15 λίτρα; Άρα, τα 15 λίτρα κοστίζουν 15 €.

Όταν κάνουμε έναν υπολογισμό με εκτίμηση – (στο περίπου όπως έλεγε και η μαμά μου!) – τη διαφορά ανάμεσα στο πραγματικό αποτέλεσμα και στο αποτέλεσμα με εκτίμηση να την ονομάζουμε σφάλμα.

Για να έχουμε όσο το δυνατό πιο ακριβή εκτίμηση, θα πρέπει να ΄χουμε όσο το δυνατόν μικρότερο σφάλμα.

Άρα για τον ίδιο αριθμό μπορείς να κάνεις διάφορες εκτιμήσεις.

Π. χ. για τον αριθμό 7,88 εκτιμούμε με μικρότερο σφάλμα αν τον θεωρήσουμε ως 7,90 και όχι 8 ή για τον αριθμό 17,17 εκτιμούμε με μικρότερο σφάλμα με το 17,20.

Συνήθως η διαφορά αυτή (σφάλμα) ανάμεσα στον ακριβή υπολογισμό και στην εκτίμηση δεν είναι σημαντική.

Π. χ. Πόσο κοστίζουν οι 4 ίδιες κονσέρβες νομάτας όταν η μία κοστίζει 0,48 €;

Εκτιμώ:

Η 1 κονσέρβα κοστίζει περίπου 0,5 ευρώ (δηλαδή μισό ευρώ)

Οι 4 κονσέρβες θα κοστίζουν 2 ευρώ (περίπου)

Υπολογίζω με ακρίβεια:

4 x 0,48 = 1,92 €

(Το σφάλμα είναι μόλις 0,08 €)

Πώς κάνω στρογγυλοποίηση;

Ελέγχω δεξιά από το ψηφίο που μου έχει ζητηθεί η στρογγυλοποίηση:

Εάν ο αριθμός είναι μεγαλύτερος ή ίσος με πέντε, γράφω τον επόμενο αριθμό.
Εάν ο αριθμός είναι μικρότερος από πέντε, το αφήνουμε όπως είναι.
Όλα τα υπόλοιπα ψηφία προς τα δεξιά τα διαγράφουμε.

Π. χ. ο 0,867 αν στρογγυλοποιηθεί στα δέκατα δηλ. στο 8, κοιτάμε τον δεξιό του αριθμό που είναι το 6. Άρα ο αριθμός θα γίνει 0,900 ή 0,9

Αν στρογγυλοποιηθεί στα εκατοστά θα γίνει 0,87 αφού ο δεξιός αριθμός των εκατοστών είναι το 7 κλπ.

Αντίθετα ο αριθμός 0,348 αν στρογγυλοποιηθεί στα δέκατα δηλ. στο 3 θα γίνει 0,300 ή 0,3 αφού ο δεξιός αριθμός από αυτόν είναι το 4 κλπ.

Πώς κάνω στρογγυλοποίηση;

[slideboom id=432402&w=425&h=370]

Δείτε την παρουσίαση του μαθήματος

(δημιουργός Π. Κώτσης)

[slideboom id=432365&w=425&h=370]

*

Δείτε…

Ώρα για εξάσκηση!

_______________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

12. Πολλαπλασιασμός δεκαδικών αριθμών

Θυμάμαι:

Εικόνα

Δείτε την παρουσίαση του μαθήματος

(δημιουργός Π. Κώτσης)

[slideboom id=438916&w=425&h=370]

Για να πολλαπλασιάσουμε ένα δεκαδικό αριθμό με 10, 100, 1.000 κτλ. μεταφέρουμε την υποδιαστολή του αντίστοιχα 1, 2, 3 κτλ. θέσεις πιο δεξιά. Όπου χρειάζεται, προσθέτουμε μηδενικά. Παραδείγματα: • 10 x 2,9 = 29 • 100 x 2,9 = 290.

Mπορώ να υπολογίσω το γινόμενο δύο αριθμών αν διπλασιάσω τον έναν και υποδιπλασιάσω συγχρόνως τον άλλο. Παράδειγμα: 1,25 x 16 = 2,5 x 8 = 5 x 4 = 20.

[slideboom id=437382&w=425&h=370]

_______________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

13. Διαίρεση ακεραίου με ακέραιο με πηλίκο δεκαδικό

Ας θυμηθούμε πώς μάθαμε να κάνουμε κάθετη διαίρεση με φυσικούς αριθμούς.

Yπολογίζω το αποτέλεσμα μιας διαίρεσης με μεγαλύτερη ακρίβεια ως εξής:

Αν αφήνει υπόλοιπο, βάζω υποδιαστολή στο πηλίκο, προσθέτω το ψηφίο 0 στο υπόλοιπο μετατρέποντάς το σε δέκατα, και συνεχίζω τη διαίρεση.
Αν ο διαιρέτης δε χωράει στο διαιρετέο, βάζω 0 στο πηλίκο και υποδιαστολή, μετατρέπω το διαιρετέο σε δέκατα και συνεχίζω τη διαίρεση.

Πολλές φορές μια διαίρεση είναι ατελής, δηλαδή τα δεκαδικά της ψηφία δεν «τελειώνουν» όσο κι αν συνεχίσω. Στην περίπτωση αυτή γράφουμε το πηλίκο της διαίρεσης με εκτίμηση.

π. χ. 167 : 23 = 7,2608695… Εκτιμούμε: 7,260

Πώς διαιρώ με το 10, 100, 1.000

Για να διαιρέσω έναν ακέραιο αριθμό με το 10,100, 1.000… για συντομία, μετακινώ την υποδιαστολή αριστερά τόσα δεκαδικά ψηφία, όσα μηδενικά έχω.

Π.χ. 2.450: 10 = 245, 0 ή 245

2.450 : 100 = 24,50

2.450 : 1.000 = 2,450

Δείτε την παρουσίαση του μαθήματος

(δημιουργός Π. Κώτσης)

[slideboom id=442084&w=425&h=370]

[slideboom id=446805&w=425&h=370]

Ώρα για εξάσκηση!

Η κ. Αγαθή αγόρασε 6 καρέκλες και πλήρωσε 165 €. Πόσο κόστιζε η μία καρέκλα ;

Πόσο ζυγίζει το ένα πακέτο βούτυρο , αν τα 1.000 πακέτα ζυγίζουν 250 κιλά ;

_________________________________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

14. Γρήγοροι πολλαπλασιασμοί και διαιρέσεις με 10, 100, 1.000

Γνωρίζω ότι:

Εικόνα

Για να διαιρέσουμε γρήγορα έναν αριθμό με 10, 100, 1.000, μεταφέρουμε αντίστοιχα την υποδιαστολή 1, 2 ή 3 θέσεις, αριστερά.

Παραδείγματα:

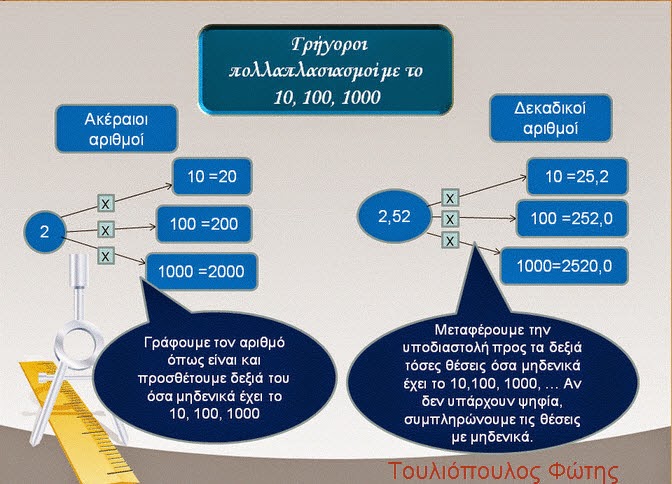
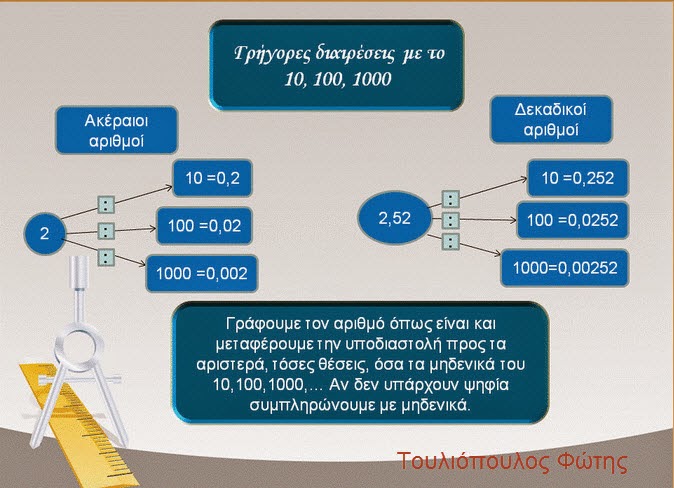Πηγή:http://e-taksh.blogspot.gr

Δείτε την παρουσίαση του μαθήματος

(Δημιουργός Γ. Σουδίας)

[slideboom id=438196&w=425&h=370]

Πάτησε στην εικόνα [κλικ]

Πηγή:Ξεκούρδιστη Τάξη

Ώρα για εξάσκηση

Πάτησε στην εικόνα [κλικ] για να παίξεις το παιχνίδι προσπαθώντας να περάσεις στην απέναντι όχθη, χωρίς να βουλιάξεις στη λίμνη

Υπολόγισε σύντομα τα γινόμενα και τα πηλίκα.

150 Χ 10 = ………….… 4.750 Χ 100 = ……………… 6.752 Χ 1.000= …………..….

1,5 Χ 10 = ………….… 4,7 Χ 100 = ……………… 5,2 Χ 1.000= …………..….

0,08 Χ 10 = ………….… 0,3 Χ 100 = ……………… 0,43 Χ 1.000= …………..….

7 : 10 = ………….… 6 : 100 = ……………… 9 : 1.000= …………..….

35 : 10 = ………….… 56 : 100 = ……………… 75 : 1.000= …………..….

8,5 : 10 = ………….… 2,5 : 100 = ……………… 6,01 : 1.000= …………..….

Συμπλήρωσε τα κενά για να ισχύουν οι ισότητες.

4,8 Χ ………… = 480                  10 Χ ………….. =6             0,05 Χ …………..= 0,5
100 Χ ………… = 2,5 0,678 Χ ………….. =67,8    1.000 Χ …………..= 500
15,5 : …….…… = 1,55               45 : ………….. = 0,45            19 : …………..= 0,019
……………. : 10 = 0,35           …….. : 100 = 6,57 …..,… : 1.000 =0,0421

Βρίσκω ότι:

το 1.200 είναι το 1/10 του ………………. το 1/10 του 500 είναι το ………………….

το 15 είναι το 1/1.000 του ………………. το 1/100 του 0,5 είναι το ………………….

το 0,4 είναι το 1/10 του ………………. το 1/1.000 του 600 είναι το ………………….

_________________________________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

36. Διαιρέτες και πολλαπλάσια

Πολλαπλάσια ενός αριθμού

Είναι οι αριθμοί που προκύπτουν αν πολλαπλασιάσουμε αυτό τον αριθμό με άλλους ακέραιους αριθμούς, π.χ. τα πολλαπλάσια του 5 είναι 1 x 5 = 5, 2 x 5 = 10, 3 x 5 = 15 κλπ.

Δύο ή περισσότεροι αριθμοί μπορούν να έχουν κοινά (ίδια) πολλαπλάσια. Μπορούμε να τα βρούμε γράφοντας τα πολλαπλάσια κάθε αριθμού με τη σειρά ή τοποθετώντας τα πολλαπλάσια κάθε αριθμού στην αριθμογραμμή ή κάνοντας πίνακα.

π.χ. τα πολλαπλάσια του 4 είναι : 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, …,

τα πολλαπλάσια του 6 είναι 6, 12, 18, 24, 3θ, 36, 42, 48, …

Άρα τα κοινά τους πολλαπλάσια είναι 12, 24, 36, ....

Τα πολλαπλάσια είναι άπειρα.

Διαιρέτες ενός αριθμού λέγονται οι φυσικοί αριθμοί με τους οποίους διαιρείται ακριβώς ο αριθμός.

Δ 10: 1, 2, 5, 10

Δ 18: 1, 2, 3, 6, 9, 18

Δ 24: 1, 2, 3, 4, 6, 8, 12, 24

Μπορώ να χρησιμοποιήσω πολλές διαφορετικές στρατηγικές (αριθμογραμμή, αντιστοίχηση, πίνακα κ.ά.) για να λύσω προβλήματα με αριθμούς που είναι πολλαπλάσια ή διαιρέτες ενός άλλου αριθμού.

Δείτε την παρουσίαση του μαθήματος

(Δημιουργός Γ. Σουδίας)

[slideboom id=499950&w=425&h=370]

_________________________________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

37. Κριτήρια διαιρετότητας του 2 του 5 και του 10

Θυμάμαι ότι:

Εικόνα

Για να διακρίνουμε εύκολα και γρήγορα αν ένας ακέραιος αριθμός διαιρείται ακριβώς από έναν άλλο, χρησιμοποιούμε ορισμένους κανόνες που ονομάζουμε κριτήρια διαιρετότητας.

Ένας ακέραιος διαιρείται ακριβώς με το 2, αν το τελευταίο του ψηφίο είναι 0 ή 2 ή 4 ή 6 ή 8 (δηλαδή ζυγός αριθμός)

Ένας ακέραιος διαιρείται ακριβώς με το 5, αν το τελευταίο του ψηφίο είναι 5 ή 0

Ένας ακέραιος διαιρείται ακριβώς με το 10, αν το τελευταίο του ψηφίο είναι 0

Καλό είναι να μάθουμε τα κριτήρια διαιρετότητας για όλους τους αριθμούς.

Ένας ακέραιος διαιρείται ακριβώς με το 3, όταν το άθροισμά των ψηφίων του είναι 3 ή 6 ή 9

Παράδειγμα: ο αριθμός 174 διαιρείται με το 3 γιατί 1+7+4=12(2+1=3), ο 969 το ίδιο γιατί 9+6+9=24(2+4=6) κλπ.

Ένας ακέραιος διαιρείται ακριβώς με το 4, όταν τα δυο τελευταία του ψηφία διαιρούνται με το 4

Π. χ. Ο 324 διαιρείται με το 4, γιατί και το 24(δύο τελευταία)είναι διαιρετό από το 4

Ένας ακέραιος διαιρείται ακριβώς με το 6 αν είναι ταυτόχρονα διαιρετός και με το 2 και με το 3

Π. χ. Ο 678 είναι διαιρετός από το 6 γιατί διαιρείται και με το 2(ζυγός) και με το 3(6+7+8=21=2+1=3)

Ένας ακέραιος διαιρείται ακριβώς με το 8, όταν οι 3 τελευταίοι αριθμοί σχηματίζουν αριθμό που διαιρείται με το 8

Π. χ. Ο 7.368 διαιρείται ακριβώς με το 8 γιατί και ο 368 διαιρείται με το 8

Ένας ακέραιος διαιρείται ακριβώς με το 9, όταν το άθροισμα των ψηφίων του δίνει 9.

Π. χ. Ο 351 διαιρείται ακριβώς με το 9 γιατί 3+5+1=9. Το ίδιο και ο 459 γιατί 4+5+9=18(8+1=9)

Ώρα για εξάσκηση

Πάτησε στην εικόνα

_________________________________________________________________________________________________________________________________________

Κάνε κλικ στην εικόνα για να διαβάσειςτο μάθημα στο βιβλίο
του μαθητή

38. Κοινά Πολλαπλάσια, Ε.Κ.Π.

Τα κοινά πολλαπλάσια δύο ή περισσότερων αριθμών είναι πολλά. Το Ε.Κ.Π. είναι το μικρότερο (Eλάχιστο) από τα Kοινά Πολλαπλάσιά τους.

Δείτε την παρουσίαση του μαθήματος

(δημιουργός Π. Κώτσης)

[slideboom id=474113&w=425&h=370]

Πώς βρίσκουμε το Ε.Κ.Π.

Α΄ τρόπος

α. Βρίσκουμε μερικά πολλαπλάσια των αριθμών.

β. Σημειώνουμε τα κοινά πολλαπλάσιά τους.

γ. Επιλέγουμε το μικρότερο – ελάχιστο από αυτά.

Β΄ τρόπος

α. Παίρνουμε τον μεγαλύτερο αριθμό. Εξετάζουμε αν είναι πολλαπλάσιο ταυτόχρονα των άλλων. Εάν είναι, αυτός είναι και το Ε.Κ.Π. Εάν δεν είναι, παίρνουμε τον διπλάσιό του και εξετάζουμε το ίδιο πράγμα. Εάν δεν είναι και πάλι πολλαπλάσιο των άλλων, παίρνουμε τον τριπλάσιό του και ελέγχουμε ξανά. Συνεχίζουμε με τον ίδιο τρόπο, μέχρι να βρούμε ένα πολλαπλάσιο του μεγαλύτερου αριθμού που να είναι πολλαπλάσιο ταυτόχρονα και των άλλων αριθμών. Αυτό θα είναι και το Ε.Κ.Π.

Παράδειγμα . Έστω ότι θέλουμε να βρούμε το ελάχιστο κοινό πολλαπλάσιο των αριθμών (2, 4, 6).

α. Παίρνουμε το μεγαλύτερο αριθμό δηλ. το 6 ελέγχουμε αν είναι πολλαπλάσιο των 2 και 4, στο παράδειγμά μας δεν είναι.

β. Διπλασιάζουμε το 6, 12= 6 χ 2 ελέγχουμε τώρα αν το 12 είναι πολλαπλάσιο των 2 και 4, πράγματι το 12 είναι πολλαπλάσιο του 2 αφού 12=2 χ 6 και ακόμα είναι και πολλαπλάσιο του 4 γιατί 12= 4 χ 3 και 12 = 6 χ 2 .Άρα Ε.Κ.Π. (2, 4, 6)=12.

Γ΄ τρόπος

Αναλύουμε όλους τους αριθμούς ταυτόχρονα σε γινόμενο πρώτων παραγόντων, με τη μέθοδο των διαδοχικών διαιρέσεων. Σταματάμε όταν το πηλίκο όλων είναι 1. Το γινόμενο όλων των πρώτων παραγόντων που εμφανίζονται είναι το Ε.Κ.Π . τους.

Παράδειγμα

Για να βρούμε το ΕΚΠ των 3, 6 και 10, αναλύουμε τους αριθμούς σε γινόμενο πρώτων παραγόντων με διαδοχικές διαιρέσεις ως εξής:

Το Ε.Κ.Π. (3, 6, 10) = 2 χ 3 χ 5 = 30

Μπορείς να κατεβάσεις το φυλλάδιο για το πώς βρίσκουμε το Ε.Κ.Π., αν πατήσεις εδώ

ΕΝΟΤΗΤΑ 2

7. Δεκαδικοί αριθμοί – Δεκαδικά κλάσματα

Ώρα για εξάσκηση!

8. Δεκαδικά κλάσματα – δεκαδικοί αριθμοί

9. Αξία θέσης ψηφίων στους δεκαδικούς αριθμούς

11. Η έννοια της στρογγυλοποίησης

Πώς κάνω στρογγυλοποίηση;

Πώς κάνω στρογγυλοποίηση;

Δείτε την παρουσίαση του μαθήματος

*

Δείτε…

Ώρα για εξάσκηση!

12. Πολλαπλασιασμός δεκαδικών αριθμών

Θυμάμαι:

Δείτε την παρουσίαση του μαθήματος

13. Διαίρεση ακεραίου με ακέραιο με πηλίκο δεκαδικό

Δείτε την παρουσίαση του μαθήματος

14. Γρήγοροι πολλαπλασιασμοί και διαιρέσεις με 10, 100, 1.000

Δείτε την παρουσίαση του μαθήματος

Ώρα για εξάσκηση

36. Διαιρέτες και πολλαπλάσια

Δείτε την παρουσίαση του μαθήματος

37. Κριτήρια διαιρετότητας του 2 του 5 και του 10

Θυμάμαι ότι:

38. Κοινά Πολλαπλάσια, Ε.Κ.Π.

Δείτε την παρουσίαση του μαθήματος

Εξασκήσου στα πολλαπλάσια [κλικ εδώ]

Αφήστε μια απάντηση Ακύρωση απάντησης