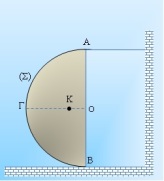
Κόβουμε ένα δίσκο μικρού πάχους, ακτίνας R = 1m κατά μήκος μιας διαμέτρου του ΑΒ. Παίρνουμε το ένα κομμάτι (Σ), μάζας Μ = 2kg και το στερεώνουμε, όπως στο σχήμα, με αβαρές νήμα, έτσι ώστε η διάμετρος ΑΒ να είναι κατακόρυφη. Αν γνωρίζουμε ότι το κέντρο μάζας του ημιδισκίου Σ, βρίσκεται πάνω στην οριζόντια ακτίνα ΟΓ, στο σημείο Κ, με  ΟΚ = d = 4R/3π, g = 10m/s² και η ροπή αδράνειας ομογενούς δίσκου ως προς άξονα κάθετο στο επίπεδό του που διέρχεται από το κέντρο του είναι Ι_δ(Ο) = 1/2 Μ_δR²

α) Σχεδιάστε τις δυνάμεις και υπολογίστε την τάση του νήματος.

β) Βρείτε τη δύναμη που ασκείται από το οριζόντιο επίπεδο, στο σημείο Β του ημιδισκίου.

γ) Ποια είναι η ελάχιστη τιμή του συντελεστή στατικής τριβής, που πρέπει να έχει το ημιδίσκιο Σ με το δάπεδο ώστε να μην ολισθαίνει;

Αν κόψουμε το νήμα παρατηρούμε ότι το ημιδίσκιο ξεκινά να κυλίεται χωρίς ολίσθηση, με το επίπεδό του να παραμένει κατακόρυφο.

δ) Ποια είναι η ροπή αδράνειάς του ως προς άξονα κάθετο στο επίπεδό του που διέρχεται από το κέντρο μάζας του Κ;

ε) Ποια θα είναι η γωνιακή ταχύτητα του ημιδισκίου τη στιγμή που η διάμετρος ΑΒ γίνεται για πρώτη φορά οριζόντια;

στ) Ποια θα είναι τότε η στροφορμή του ημιδισκίου, ως προς τον οριζόντια άξονα που διέρχεται από το κέντρο του Ο;

Απάντηση(Pdf)

Ένας κύλινδρος μάζας M = 6kg και ακτίνας R = 10cm ηρεμεί πάνω σε οριζόντια σανίδα ΑΒ μάζας m = 3kg. Ο συντελεστής στατικής τριβής ανάμεσα στον κύλινδρο και τη σανίδα είναι μ_s = 0,1. Τη χρονική στιγμή t =0, που το κέντρο μάζας του κυλίνδρου βρίσκεται στην κατακόρυφο που περνάει από το άκρο Α της σανίδας, ασκούμε στο κέντρο μάζας του κυλίνδρου οριζόντια σταθερή δύναμη μέτρου F = 5N. Παρατηρούμε ότι ο κύλινδρος κυλίεται χωρίς ολίσθηση πάνω στη σανίδα. Δίνεται η ροπή αδράνειας του δίσκου ως προς τον άξονα περιστροφής του I_cm = ½ MR² και g = 10m/s².

α) Σχεδιάστε τη στατική τριβή στο δίσκο και στη σανίδα εξηγώντας τη φορά τους. Τι κίνηση θα κάνει η σανίδα;

β) Βρείτε το μέτρο της στατικής τριβής που ασκείται στον κύλινδρο.

γ) Ποια είναι η μέγιστη τιμή του μέτρου της δύναμης F, ώστε ο κύλινδρος να μην ολισθαίνει πάνω στη σανίδα;

δ) Υπολογίστε το μέτρο της επιτάχυνσης της σανίδας, της επιτάχυνσης του κέντρου μάζας του κυλίνδρου και της γωνιακής επιτάχυνσης του κυλίνδρου.

ε) Πότε θα φτάσει ο κύλινδρος στο άκρο Β της σανίδας και πόσες στροφές θα εκτελέσει;

στ) Ποιες ενεργειακές μετατροπές συμβαίνουν;

Το δάπεδο πάνω στο οποίο βρίσκεται η σανίδα θεωρείται λείο.

Απάντηση(Word)

Απάντηση(Pdf)

Διαθέτουμε ένα στερεό το οποίο αποτελείται από μια ομογενή ράβδο ΟΚ, μήκους l=2m και μάζας m=15kg, και, έναν ομογενή δίσκο μάζας Μ=40kg και ακτίνας R=1m απόλυτα συνδεδεμένο με τη ράβδο, με το άκρο Κ της ράβδου να είναι και το κέντρο του δίσκου. Το στερεό S μπορεί να στρέφεται χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα ο οποίος διέρχεται από το άκρο Ο της ράβδου, ενώ συγκρατείται με την ράβδο σε οριζόντια θέση, όπως στο σχήμα.

i) Σε μια στιγμή αφήνουμε ελεύθερο το στερεό να περιστραφεί.

α) Να υπολογιστεί η ροπή αδράνειας του στερεού S, ως προς τον άξονα περιστροφής.

β) Να υπολογιστεί η αρχική γωνιακή επιτάχυνση του στερεού S, καθώς και  η επιτάχυνση του κέντρου Κ του δίσκου.

ii) Κόβουμε και απομακρύνουμε τον μισό δίσκο, οπότε παίρνουμε το στερεό S₁, όπως φαίνεται στο δεύτερο σχήμα.

α) Στηριζόμενοι στον ορισμό της ροπής αδράνειας, να υπολογίσετε  τη ροπή αδράνειας Ι₁ του στερεού S₁, ως προς τον άξονα περιστροφής στο Ο, εκμεταλλευόμενοι την ροπή αδράνειας του στερεού S.

β) Αν αφήσουμε το στερεό S₁ να κινηθεί ξανά, από την θέση που η ράβδος είναι οριζόντια, να υπολογιστούν η αρχική γωνιακή επιτάχυνση του στερεού και η αρχική επιτάχυνση του σημείου Κ.

Δίνεται η ροπή αδράνειας ενός ομογενούς δίσκου ως προς κάθετο άξονα ο οποίος περνά από το κέντρο του Ι₁=1/2 ΜR² και η αντίστοιχη ροπή αδράνειας για την ομογενή ράβδο Ι₂= ml²/12 και g=10m/s².

Απάντηση:

ή

 Και αν πάρουμε το μισό δίσκο;

Η ομογενής και ισοπαχής ράβδος μήκους d του διπλανού σχήματος, αφήνεται να στηριχθεί με το ένα άκρο της σε λείο κατακόρυφο τοίχο και με το άλλο άκρο της σε οριζόντιο δάπεδο. Η ράβδος τοποθετείται σε κατακόρυφο επίπεδο ( της σελίδας / οθόνης ) έτσι ώστε να σχηματίσει γωνία θ με το δάπεδο τέτοια ώστε ημθ = 0,8 και αφήνεται ελεύθερη. Ο συντελεστής οριακής τριβής με το δάπεδο είναι …..

Η συνέχεια εδώ…

Μια εναλλακτική μέθοδος, στο 2ο ερώτημα – όχι για μαθητές – ΕΔΩ

Το καζανάκι της τουαλέτας μιας κατοικίας, τροφοδοτείται από μεγάλη ανοιχτή δεξαμενή  στην ταράτσα, στην οποία η στάθμη του νερού βρίσκεται σε σταθερό ύψος Η = 3,2m από το σωληνάκι τροφοδοσίας (Σ), όπως φαίνεται στο σχήμα 1. Αν g = 10m/s², το νερό θεωρηθεί ιδανικό ρευστό και η ροή στρωτή και μόνιμη:

i) Ποια είναι η ταχύτητα και η αντίστοιχη παροχή του νερού, που μπαίνει στο καζανάκι, από την τρύπα του πλαϊνού τοιχώματος

α) όσο η στάθμη βρίσκεται κάτω από την τρύπα (σχ. 1α);

β) τη στιγμή που η στάθμη βρίσκεται σε ύψος h = 0,4m πάνω από την τρύπα (σχ. 1β);

ii) Το σωληνάκι (Σ) έχει εμβαδό διατομής A = 2cm² και θέλουμε να σταματάει την τροφοδοσία, όταν η στάθμη του νερού φτάσει σε ύψος h πάνω από την τρύπα. Για το σκοπό αυτό υπάρχει ένας μηχανισμός, που αποτελείται από δύο – κολλημένες μεταξύ τους – αβαρείς ράβδους ΚΟ και ΟΛ με OK ┴ OΛ (σχήμα 2). Στο άκρο Κ έχουμε συνδέσει, με άρθρωση, μια πλαστική σφαίρα (πλωτήρας), ενώ στο άκρο Λ επίσης με άρθρωση, έχει συνδεθεί κυλινδρική τάπα εμβαδού . Ο μηχανισμός μπορεί να στρέφεται περί οριζόντιο άξονα, που διέρχεται από το Ο, έτσι ώστε οι ράβδοι και τα κέντρα σφαίρας και τάπας, βρίσκονται διαρκώς στο ίδιο κατακόρυφο επίπεδο. Όταν η στάθμη του νερού φτάσει στο επιθυμητό όριο, η σφαίρα παραμένει βυθισμένη σε ποσοστό 20% του όγκου της στο νερό και η τάπα σφραγίζει την τρύπα διακόπτοντας την παροχή νερού.

Αν (ΟΚ) = 2(OΛ), υπολογίστε το μέτρο

α) της άνωσης που δέχεται η σφαίρα και

β) της δύναμης που δέχεται ο μηχανισμός από την άρθρωση Ο.

iii) Ποια πρέπει να είναι η ακτίνα της σφαίρας;

Απάντηση(Word)

Απάντηση(Pdf)

i) Υποθέτουμε ότι ο δίσκος μπορεί να περιστρέφεται περί σταθερό άξονα zz΄, κάθετο στο επίπεδό του, που διέρχεται από το κέντρο του Ο.

Συνέχεια(Pdf)