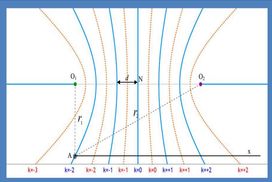
Σωματίδιο μάζας m = 10-27kg και φορτίου q = 10-19C εκτοξεύεται με ταχύτητα οριζόντιας διεύθυνσης και εισέρχεται στο σημείο Α, στο εσωτερικό οριζόντιου ρευματοφόρου σωληνοειδούς απείρου μήκους, όπως φαίνεται στο σχήμα, κάθετα στις δυναμικές γραμμές του μαγνητικού πεδίου. Το μαγνητικό πεδίο κυκλικής διατομής, κέντρου Ο, έχει ακτίνα R = 0,2m και η γωνία που σχηματίζει η διεύθυνση της ταχύτητας με την ακτίνα ΟΑ είναι θ = π/6 rad. Το σωληνοειδές έχει n = 104 σπείρες/m και διαρρέεται από ρεύμα έντασης Ι = 25/πΑ. Η τροχιά του σωματιδίου διέρχεται από το κέντρο Ο του κύκλου. Δίνεται μ0/4π = 10-7Ν/Α2 και ότι στο εξωτερικό του σωληνοειδούς το μαγνητικό πεδίο είναι μηδενικό.
i) Βρείτε το μέτρο και την κατεύθυνση της έντασης του ομογενούς μαγνητικού πεδίου στο εσωτερικό του σωληνοειδούς.
ii) Ποιο πρέπει να είναι το μέτρο υ0 της ταχύτητας του σωματιδίου;
iii) Ποια είναι η μεταβολή της ορμής του σωματιδίου στη διαδρομή ΑΟ;
iv) Πόσο χρόνο θα χρειαστεί το σωματίδιο για να διανύσει το τόξο ΑΟ;
v) Αν η ταχύτητα εισόδου του σωματιδίου στο μαγνητικό πεδίο διπλασιαστεί, ο χρόνος για να διανύσει το τόξο ΑΟ
α. θα διπλασιαστεί
β. θα υποδιπλασιαστεί
γ. θα παραμείνει σταθερός.
Δικαιολογείστε τη σωστή απάντηση.





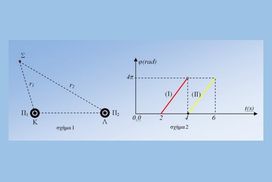
 Διαθέτουμε δυο λεπτά σύρματα Σ1 και Σ2 πολύ μεγάλου μήκους. Τα κάμπτουμε ώστε να δημιουργήσουμε δυο αγωγούς, τους οποίους συνδέουμε σε σειρά όπως στο σχήμα 1. Ο αγωγός Σ που σχηματίζεται έχει ένα ημικύκλιο ακτίνας R και δυο ημιευθείες Αx, Γy. Όταν διαρρέει τον αγωγό Σ ρεύμα έντασης I, η ένταση του μαγνητικού πεδίου στο κέντρο Ο του ημικυκλίου είναι B. Αποσυνδέουμε το σύστημα, κάμπτουμε εκ νέου τα σύρματα σε σχήμα ορθής γωνίας, τα τοποθετούμε όπως στο σχήμα 2 και τα τροφοδοτούμε με ρεύμα ίδιας έντασης Ι΄. Στο ευθύγραμμο τμήμα ΔΚ, που συνδέει τις κορυφές των ορθών γωνιών το σημείο Ο είναι μέσον με ΔΟ = ΟΚ = R. Αφού βρείτε τη φορά του ρεύματος σε κάθε αγωγό, υπολογίστε ποια από τις παρακάτω είναι η τιμή της έντασης Ι΄, ώστε στο σημείο Ο το μαγνητικό πεδίο να έχει πάλι ένταση B.
Διαθέτουμε δυο λεπτά σύρματα Σ1 και Σ2 πολύ μεγάλου μήκους. Τα κάμπτουμε ώστε να δημιουργήσουμε δυο αγωγούς, τους οποίους συνδέουμε σε σειρά όπως στο σχήμα 1. Ο αγωγός Σ που σχηματίζεται έχει ένα ημικύκλιο ακτίνας R και δυο ημιευθείες Αx, Γy. Όταν διαρρέει τον αγωγό Σ ρεύμα έντασης I, η ένταση του μαγνητικού πεδίου στο κέντρο Ο του ημικυκλίου είναι B. Αποσυνδέουμε το σύστημα, κάμπτουμε εκ νέου τα σύρματα σε σχήμα ορθής γωνίας, τα τοποθετούμε όπως στο σχήμα 2 και τα τροφοδοτούμε με ρεύμα ίδιας έντασης Ι΄. Στο ευθύγραμμο τμήμα ΔΚ, που συνδέει τις κορυφές των ορθών γωνιών το σημείο Ο είναι μέσον με ΔΟ = ΟΚ = R. Αφού βρείτε τη φορά του ρεύματος σε κάθε αγωγό, υπολογίστε ποια από τις παρακάτω είναι η τιμή της έντασης Ι΄, ώστε στο σημείο Ο το μαγνητικό πεδίο να έχει πάλι ένταση B.