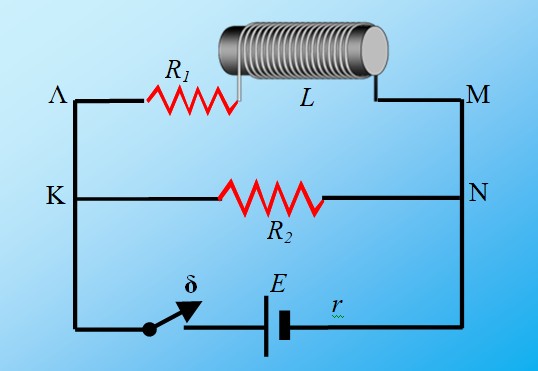
 Στο κύκλωμα του σχήματος δίνονται R1 = 3Ω, R2 = 6Ω, η πηγή ιδανική με ΗΕΔ Ε = 12V και το πηνίο ιδανικό με συντελεστή αυτεπαγωγής L = 0,3H.
Στο κύκλωμα του σχήματος δίνονται R1 = 3Ω, R2 = 6Ω, η πηγή ιδανική με ΗΕΔ Ε = 12V και το πηνίο ιδανικό με συντελεστή αυτεπαγωγής L = 0,3H.
i) Τη χρονική στιγμή t0 = 0s κλείνουμε το διακόπτη δ και τον ανοίγουμε ακαριαία τη χρονική στιγμή t1 = 1s. Δεδομένου ότι το χρονικό αυτό διάστημα είναι αρκετό για την αποκατάσταση του ρεύματος, βρείτε την ένταση του ρεύματος σε κάθε κλάδο του κυκλώματος και την αλγεβρική τιμή της ΗΕΔ αυτεπαγωγής στο πηνίο
α) τη χρονική στιγμή t = 0+s (ποσοτικά)
β) μια χρονική στιγμή 0s < t < 1s (ποιοτικά)
γ) τη χρονική στιγμή t = 1s (ποσοτικά)
ii) Μετά το άνοιγμα του διακόπτη και με δεδομένο ότι τη χρονική στιγμή t2 = 2s έχει τελειώσει το φαινόμενο της αυτεπαγωγής, βρείτε την ένταση του ρεύματος σε κάθε κλάδο του κυκλώματος και την αλγεβρική τιμή της ΗΕΔ αυτεπαγωγής στο πηνίο
α) τη χρονική στιγμή t = 1+s (ποσοτικά)
β) Μια χρονική στιγμή 1s < t < 2s (ποιοτικά)
γ) τη χρονική στιγμή t = 2s (ποσοτικά)
iii) Να κάνετε τη γραφική παράσταση της έντασης του ρεύματος σε συνάρτηση με το χρόνο, που διαρρέει κάθε κλάδο του κυκλώματος πριν και μετά το άνοιγμα του διακόπτη.
iv) Να κάνετε τη γραφική παράσταση της ΗΕΔ αυτεπαγωγής στο πηνίο σε συνάρτηση με το χρόνο, πριν και μετά το άνοιγμα του διακόπτη.
v) Κάποια στιγμή t1 όπου 0s < t1 < 1s η ένταση του ρεύματος που δίνει η πηγή είναι i = 3A. Βρείτε τις ενεργειακές μετατροπές, υπολογίζοντας την ισχύ που ανταλλάσσει με το κύκλωμα κάθε δίπολο του κυκλώματος.
vi) Κάποια στιγμή t1 όπου 1s < t2 < 2s η ένταση του ρεύματος που διαρρέει το κύκλωμα είναι i1 = 3A. Βρείτε τις ενεργειακές μετατροπές, υπολογίζοντας την ισχύ που ανταλλάσσει με το κύκλωμα κάθε δίπολο του κυκλώματος.






 Το κύκλωμα του σχήματος περιλαμβάνει ιδανική πηγή με ΗΕΔ Ε = 100V, ιδανικό πηνίο με συντελεστή αυτεπαγωγής L = 0,1H και αντίσταση R = 10Ω, συνδεδεμένα σε σειρά. Τη χρονική στιγμή t0 = 0 κλείνουμε το διακόπτη δ.
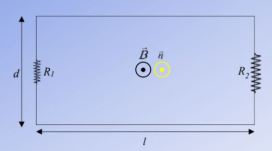
Το κύκλωμα του σχήματος περιλαμβάνει ιδανική πηγή με ΗΕΔ Ε = 100V, ιδανικό πηνίο με συντελεστή αυτεπαγωγής L = 0,1H και αντίσταση R = 10Ω, συνδεδεμένα σε σειρά. Τη χρονική στιγμή t0 = 0 κλείνουμε το διακόπτη δ. Θεωρούμε ένα συρμάτινο τριγωνικό πλαίσιο ΚΜΝ με (ΜΝ) = l = 1m, που μπορεί να στρέφεται περί άξονα, διερχόμενο από το άκρο του Κ και είναι κάθετος στο επίπεδό του. Για τη σταθερότητα της κατασκευής, μια ράβδος από μονωτικό υλικό, μήκους επίσης l, συμπίπτει με το ύψος ΚΛ του τριγώνου και ορίζει στη ΜΝ τμήματα με (ΜΛ)/(ΛΝ) = α/β = 3/7 (σχήμα 1)
Θεωρούμε ένα συρμάτινο τριγωνικό πλαίσιο ΚΜΝ με (ΜΝ) = l = 1m, που μπορεί να στρέφεται περί άξονα, διερχόμενο από το άκρο του Κ και είναι κάθετος στο επίπεδό του. Για τη σταθερότητα της κατασκευής, μια ράβδος από μονωτικό υλικό, μήκους επίσης l, συμπίπτει με το ύψος ΚΛ του τριγώνου και ορίζει στη ΜΝ τμήματα με (ΜΛ)/(ΛΝ) = α/β = 3/7 (σχήμα 1)