Κατηγορία: 4.03 Ταλαντώσεις

Όπως φαίνεται δεξιά, έχουμε ως δεδομένα:

• μάζα ταλαντωτή m = 2kg,
• σταθερά επαναφοράς k = 36N/m,
• σταθερά απόσβεσης b = 12kg/s.

Ο ταλαντωτής τη χρονική στιγμή t₀ = 0s, έχει αρχική απομάκρυνση A₀ = 0,4m και αρχική ταχύτητα υ₀ = 0m/s.

α) Υπολογίστε την γωνιακή ιδιοσυχνότητα ω₀ και την ιδιοπερίοδο Τ₀ της αντίστοιχης αμείωτης ταλάντωσης. Από το διάγραμμα βρείτε πόση είναι η περίοδος της φθίνουσας ταλάντωσης. Τι συμπεραίνετε για τη σχέση μεταξύ τους;

Συνέχεια 

Συνέχεια 

Θέτουμε σε απλή αρμονική ταλάντωση, δυο σώματα Σ₁ και Σ₂ με ίσες μάζες m₁ = m₂ = m. Στο σχήμα φαίνονται τα αντίστοιχα διαγράμματα p → x (ορμής – θέσης), όπου A₁ = 2A₂ και p_max,1 = p_max,2

 i) Γιατί έχουν αυτή τη μορφή οι γραφικές παραστάσεις p → x;

ii) Ο λόγος ω₁/ω₂ των γωνιακών συχνοτήτων είναι

α) 4     β) 2      γ) 1/2

iii) Ο λόγος Ε₁/Ε₂ των ενεργειών ταλάντωσης είναι

α) 1      β) 1/2   γ) 1/4

iv) Αν η αρχική φάση και των δυο ταλαντώσεων είναι μηδέν, να κάνετε ποιοτικά σε κοινούς άξονες τις γραφικές παραστάσεις

x → t, p → t, U → t, K → t από 0 ≤ t ≤ T₁

Απάντηση 

Απάντηση 

Υλικό σημείο μάζας m = 1kg, εκτελεί αρμονική ταλάντωση με εξίσωση x = 0,5∙ημ(10t) (S.I.)

Α) Αν είναι απλή αρμονική ταλάντωση:

i) Βρείτε τις χρονικές εξισώσεις υ(t), a(t), ΣF(t), K(t), U(t), E_T(t), P_ΣF(t)

ii) Να κάνετε τις γραφικές παραστάσεις

α) K(t), U(t), E_T(t) σε ένα διάγραμμα και

β) σε ένα άλλο διάγραμμα την P_ΣF(t)

από t₀ = 0s, ως t₁ = π/5 s

iii) Υπολογίστε το έργο της συνισταμένης δύναμης από t₀ = 0s, ως t₁ = π/10 s

Β) Αν είναι εξαναγκασμένη αρμονική ταλάντωση με δύναμη απόσβεσης της μορφής
F = -2υ (S.I.) και γωνιακής ιδιοσυχνότητας ω₀ = 8 rad/s:

Συνέχεια 

Θέμα Α

Ένα σώμα μάζας m εκτελεί α.α.τ. σε οριζόντιο λείο δάπεδο και κατά τη διάρκεια της ταλάντωσης η μέγιστη επιτάχυνση που επιτυγχάνει έχει μέτρο a_max. Αν το πλάτος της ταλάντωσης είναι Α, η ενέργεια της ταλάντωσης είναι:

α) Ε = ½ ma_maxA           β) Ε = ma_maxA               γ) Ε = ¼ ma_maxA

Επιλέξτε τη σωστή απάντηση και δικαιολογείστε την επιλογή σας.

Θέμα Β

Ένα σώμα μάζας m = 0,25kg είναι στερεωμένο στην κορυφή ενός κατακόρυφου ελατηρίου που είναι αγκυρωμένο στο πάτωμα. Το φυσικό μήκος του ελατηρίου είναι l₀ = 8cm και το μήκος του ελατηρίου όταν το σώμα βρίσκεται σε ισορροπία είναι l₁ = 5,5cm. Όταν το σώμα ηρεμεί στη θέση ισορροπίας του, του δίνεται ένα απότομο χτύπημα προς τα κάτω με σφυρί, έτσι ώστε η αρχική του ταχύτητα να έχει μέτρο υ₀ = 0,4m/s.

i) Σε ποιο μέγιστο ύψος πάνω από το δάπεδο υψώνεται κάθε φορά το σώμα; Το ελατήριο φτάνει στο φυσικό του μήκος κατά τη διάρκεια της ταλάντωσης; Ποια ελάχιστη αρχική ταχύτητα πρέπει να δοθεί στο σώμα ώστε το ελατήριο να φτάνει οριακά το φυσικό του μήκος;

ii) Πόσος χρόνος χρειάζεται για να φτάσει το σώμα στο μέγιστο ύψος του για πρώτη φορά;

iii) Να γράψετε τη χρονική εξίσωση της αλγεβρικής τιμής της δύναμης του ελατηρίου σε συνάρτηση με το χρόνο και να κάνετε την αντίστοιχη γραφική παράσταση για μια περίοδο.

iv) Να βρείτε σε συνάρτηση με την απομάκρυνση, τις εξισώσεις: Ενέργειας ταλάντωσης, Δυναμικής Ενέργειας ταλάντωσης, Κινητικής Ενέργειας, Βαρυτικής Δυναμικής Ενέργειας (με επίπεδο αναφοράς τη θέση ισορροπίας) και Δυναμικής Ενέργειας ελατηρίου.

v) Να κάνετε στο ίδιο σύστημα αξόνων τις γραφικές παραστάσεις Ενέργειας ταλάντωσης, Δυναμικής Ενέργειας ταλάντωσης, Κινητικής Ενέργειας, Βαρυτικής Δυναμικής Ενέργειας (με επίπεδο αναφοράς τη θέση ισορροπίας) και Δυναμικής Ενέργειας ελατηρίου, σε συνάρτηση με την απομάκρυνση. Δίνεται g = 10m/s².

Συνέχεια στο γκισέ 

Συνέχεια στο γκισέ 

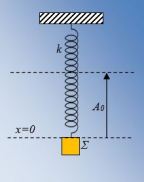Στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου, σταθεράς k = 100N/m, που το πάνω άκρο του είναι ακλόνητα δεμένο στο ταβάνι, είναι προσαρμοσμένο σώμα, μάζας m = 1kg και ισορροπεί ακίνητο. Απομακρύνουμε το σώμα κατά A₀ = 2m, από τη θέση ισορροπίας και το αφήνουμε ελεύθερο, χωρίς αρχική ταχύτητα. Εκτός από τη δύναμη επαναφοράς F=-kx , υπάρχει δύναμη τριβής αντίθετη της ταχύτητας της μορφής F=-bυ .Το σώμα εκτελεί φθίνουσα ταλάντωση με σταθερά απόσβεσης b = 2kg/s, η οποία θεωρείται «μικρή» για τις συνθήκες του προβλήματος.

Η συνέχεια…

Απάντηση 

Σώμα Σ μάζας  Μ = 4kg, ισορροπεί ακίνητο, δεμένο στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου, σταθεράς k = 400N/m, το άλλο άκρο του οποίου είναι ακλόνητα στερεωμένο στο ταβάνι. Τη χρονική στιγμή t₀ = 0, εκτοξεύουμε το σώμα με αρχική ταχύτητα υ₀, κατακόρυφη προς τα πάνω, οπότε αυτό εκτελεί α.α.τ. πλάτους Α = 0,5m.

i) Υπολογίστε την περίοδο της ταλάντωσης και το μέτρο της ταχύτητας εκτόξευσης.

ii) Γράψτε τις χρονικές εξισώσεις της απομάκρυνσης και της ταχύτητας αυτής της ταλάντωσης. Θεωρείστε θετική φορά του άξονα της κίνησης προς τα πάνω.

iii) Να γίνει η γραφική παράσταση του ρυθμού μεταβολής της δυναμικής ενέργειας της ταλάντωσης σε συνάρτηση με το χρόνο,  για μια περίοδο της κίνησης.

iv) Κάποια στιγμή που το σώμα κατέρχεται, το ελατήριο είναι συσπειρωμένο και το σύστημα ελατήριο-σώμα έχει αποθηκεύσει δυναμική ενέργεια παραμόρφωσης U_ελ = 18J. Με μια εσωτερική έκρηξη, που διαρκεί αμελητέο χρόνο, το σώμα Σ διασπάται σε δύο κομμάτια Σ₁ και Σ₂ μαζών m₁ και m₂ με m₂ = 3m₁. Το Σ₁ παραμένει κολλημένο στο ελατήριο και ακινητοποιείται στιγμιαία, ενώ το Σ₂ εκτοξεύεται προς τα κάτω με ταχύτητα υ₂ .
Να υπολογίσετε:
α) την ταχύτητα του σώματος Σ λίγο πριν τη διάσπαση.
β) την ταχύτητα του σώματος Σ₂ αμέσως μετά τη διάσπαση.
γ) το ποσοστό αύξησης της κινητικής ενέργειας του συστήματος εξαιτίας της διάσπασης.
v) Το σώμα Σ₁ εκτελεί νέα α.α.τ. Γράψτε την εξίσωση της αλγεβρικής τιμής της δύναμης του ελατηρίου σε συνάρτηση με το χρόνο, θεωρώντας εκ νέου t₀ = 0, τη στιγμή της διάσπασης και κάνετε την αντίστοιχη γραφική παράσταση για μια περίοδο.

Απάντηση 

Απάντηση