Στο λάστιχο ενός τροχού αυτοκινήτου έχει σφηνώσει ένα χαλίκι Λ, μάζας m =10g. Η διάμετρος του ελαστικού είναι δ = 15,8 inch ≈ 40cm, το αυτοκίνητο κινείται με ταχύτητα υ = 72km/h και ο τροχός κυλίεται χωρίς ολίσθηση.
i) Αν ο τροχός θεωρηθεί επίπεδος δίσκος, ποια είναι η στροφορμή του χαλικιού ως προς το κέντρο Ο του τροχού; Σχεδιάστε το διάνυσμα. Αν το αυτοκίνητο κινείται προς την Ανατολή, ποιον προσανατολισμό έχει το διάνυσμα;
ii) α) Ποια είναι η στροφορμή ως προς τον άξονα Ζ΄Ζ περιστροφής του δίσκου;
β) Θεωρείστε ένα σημείο Α του άξονα, που απέχει από το Ο απόσταση ΟΑ = 15cm. Υπολογίστε τη στροφορμή του χαλικιού ως προς αυτό το σημείο και σχεδιάστε το διάνυσμά της. Τι συμπεραίνετε; Η στροφορμή είναι ίδια ως προς οποιοδήποτε σημείο του άξονα;
iii) Υπολογίστε την προβολή του διανύσματος του ερωτήματος (iiβ), πάνω στον άξονα Z΄Z. Τι παρατηρείτε;
iv) Κάποια στιγμή t1, που το χαλίκι διέρχεται από την ανώτερη θέση, χάνει την επαφή του με το λάστιχο και εκτοξεύεται οριζόντια. Για τη χρονική στιγμή t1 + dt, όπου dt → 0, χαρακτηρίστε παρακάτω προτάσεις ως σωστές ή λανθασμένες:
α) Το χαλίκι δεν κάνει πλέον κυκλική κίνηση, άρα αμέσως μετά την εκτόξευση η στροφορμή του μηδενίζεται.
β) Δεν έχει στροφορμή ένα υλικό σημείο, που εκτελεί μεταφορική κίνηση.
γ) Η στροφορμή του χαλικιού δεν «χάνεται» ξαφνικά, έτσι αμέσως μετά την αποκόλληση είναι ίδια με αμέσως πριν.
v) Τη χρονική στιγμή t1 χαρακτηρίστε τις παρακάτω προτάσεις ως σωστές ή λανθασμένες:
α) Η στροφορμή του χαλικιού είναι 0,04kgm2/s.
β) Η στροφορμή του χαλικιού ως προς το σημείο Ο ή ως προς τον άξονα Ζ΄Ζ είναι 0,04kgm2/s.
γ) Η στροφορμή του χαλικιού ως προς το σημείο Ο ή ως προς τον άξονα Ζ΄Ζ έχει μέτρο 0,04kgm2/s.
δ) Η στροφορμή του χαλικιού, ως προς ένα τυχαίο σημείο Γ του εδάφους, που βρίσκεται στο ίδιο κατακόρυφο επίπεδο με το χαλίκι, έχει μέτρο 0,16kgm2/s.
vi) Τι κίνηση θα κάνει το χαλίκι μέχρι να φτάσει στο έδαφος και ποιος είναι ο ρυθμός μεταβολής της στροφορμής του ως προς το σημείο Γ του εδάφους, όταν βρίσκεται σε ύψος h = R από το έδαφος; Δίνεται g = 10m/s.2
Απάντηση 
Απάντηση 
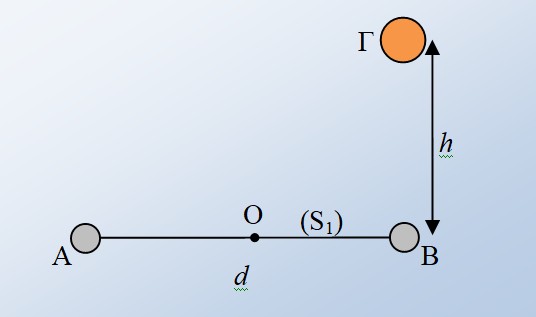 Δύο μικρές όμοιες σφαίρες Α και Β μάζας m, είναι στερεωμένες στα άκρα μιας αβαρούς ράβδου μήκους d, δημιουργώντας έτσι το σώμα S1, το οποίο ηρεμεί σε οριζόντια διεύθυνση. Η ράβδος μπορεί να στρέφεται ελεύθερα γύρω από οριζόντιο άξονα που διέρχεται από άρθρωση στο μέσον της Ο. Μια άλλη σφαίρα Γ μάζας επίσης m αφήνεται ελεύθερη από ύψος h κατακόρυφα πάνω από τη σφαίρα Β και συγκρούεται με αυτήν κεντρικά και πλαστικά. Δημιουργείται έτσι ένα στερεό S2 , που στρέφεται περί το σημείο Ο. Η χρονική διάρκεια της κρούσης θεωρείται dt → 0 και επίπεδο αναφοράς βαρυτικής δυναμικής ενέργειας παίρνουμε το οριζόντιο επίπεδο της ράβδου ΑΒ.
Δύο μικρές όμοιες σφαίρες Α και Β μάζας m, είναι στερεωμένες στα άκρα μιας αβαρούς ράβδου μήκους d, δημιουργώντας έτσι το σώμα S1, το οποίο ηρεμεί σε οριζόντια διεύθυνση. Η ράβδος μπορεί να στρέφεται ελεύθερα γύρω από οριζόντιο άξονα που διέρχεται από άρθρωση στο μέσον της Ο. Μια άλλη σφαίρα Γ μάζας επίσης m αφήνεται ελεύθερη από ύψος h κατακόρυφα πάνω από τη σφαίρα Β και συγκρούεται με αυτήν κεντρικά και πλαστικά. Δημιουργείται έτσι ένα στερεό S2 , που στρέφεται περί το σημείο Ο. Η χρονική διάρκεια της κρούσης θεωρείται dt → 0 και επίπεδο αναφοράς βαρυτικής δυναμικής ενέργειας παίρνουμε το οριζόντιο επίπεδο της ράβδου ΑΒ.










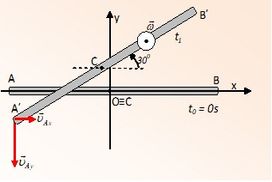 Κάποια χρονική στιγμή t1 βρίσκεται για πρώτη φορά στη θέση του διπλανού σχήματος, έχοντας στραφεί αντιωρολογιακά κατά Δθ = 300.
Κάποια χρονική στιγμή t1 βρίσκεται για πρώτη φορά στη θέση του διπλανού σχήματος, έχοντας στραφεί αντιωρολογιακά κατά Δθ = 300.
 Δύο υλικά σημεία Σ1 και Σ2 κινούνται σε περιοχή χωρίς βαρυτικές επιδράσεις, πάνω στο επίπεδο xOy. Το Σ1 κινείται παράλληλα στον άξονα Ox και το Σ2 παράλληλα στον άξονα Oy, όπως φαίνεται στο σχήμα. Στη θέση που τα βλέπουμε, ασκείται στο Σ1 η (εξωτερική) δύναμη μέτρου |F| = 2N, με θ = 300. Το Σ1 έχει μάζα m1 = 6kg και μέτρο ταχύτητας υ1 = 2m/s, ενώ το Σ1 έχει μάζα m2 = 3kg και μέτρο ταχύτητας υ2 = 4m/s. Οι αποστάσεις που φαίνονται στο σχήμα, από την αρχή Ο του συστήματος των αξόνων είναι r1 = 1,5m, r2 =3m. Τα διανύσματα των ταχυτήτων και η δύναμη ανήκουν στο επίπεδο xOy. Θεωρώντας θετική φορά από τη σελίδα προς τον αναγνώστη υπολογίστε:
Δύο υλικά σημεία Σ1 και Σ2 κινούνται σε περιοχή χωρίς βαρυτικές επιδράσεις, πάνω στο επίπεδο xOy. Το Σ1 κινείται παράλληλα στον άξονα Ox και το Σ2 παράλληλα στον άξονα Oy, όπως φαίνεται στο σχήμα. Στη θέση που τα βλέπουμε, ασκείται στο Σ1 η (εξωτερική) δύναμη μέτρου |F| = 2N, με θ = 300. Το Σ1 έχει μάζα m1 = 6kg και μέτρο ταχύτητας υ1 = 2m/s, ενώ το Σ1 έχει μάζα m2 = 3kg και μέτρο ταχύτητας υ2 = 4m/s. Οι αποστάσεις που φαίνονται στο σχήμα, από την αρχή Ο του συστήματος των αξόνων είναι r1 = 1,5m, r2 =3m. Τα διανύσματα των ταχυτήτων και η δύναμη ανήκουν στο επίπεδο xOy. Θεωρώντας θετική φορά από τη σελίδα προς τον αναγνώστη υπολογίστε: