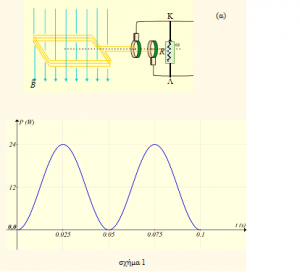
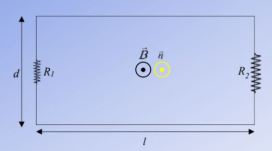
Ένα σωληνοειδές «απείρου μήκους» με πυκνότητα σπειρών n = 2500σπείρες/m, διαρρέεται από ρεύμα έντασης Ι = √2/πΑ. Η διάμετρος κάθε σπείρας είναι Δ = 60cm. Θεωρούμε ότι εξωτερικά του σωληνοειδούς, δεν υφίσταται μαγνητικό πεδίο, ενώ στο εσωτερικό του το μαγνητικό πεδίο είναι ομογενές. Ένα ηλεκτρόνιο μάζας m = 9∙10-31kg και φορτίου q = -1,6∙10-19C, επιταχύνεται από την ηρεμία μεταξύ δύο σημείων Α και Γ, με VΑΓ = -16∙103V και αμέσως εισέρχεται στο σωληνοειδές σε διεύθυνση, που διέρχεται από τον άξονα του σωληνοειδούς κάθετα σε αυτόν. Το σωματίδιο αποκλίνει από την αρχική του διεύθυνση κίνησης και εξέρχεται από το σωληνοειδές σε σημείο Δ. Στο παρακάτω σχήμα, φαίνεται μια κάθετη τομή του σωληνοειδούς.
Δίνεται μ0 = 4π∙10-7 Ν/Α2και ότι δεν έχουμε σχετικιστικά φαινόμενα.
α) Βρείτε την κατεύθυνση του ηλεκτρικού πεδίου και το μέτρο υΓ της ταχύτητας του ηλεκτρονίου στο σημείο Γ.
β) Σχεδιάστε στο σχήμα τη φορά της έντασης του μαγνητικού πεδίου στο εσωτερικό του σωληνοειδούς και τη φορά του ρεύματος σε κάθε σπείρα. Ποιο είναι το μέτρο της έντασης αυτού του μαγνητικού πεδίου;
γ) Να βρείτε τη γωνία απόκλισης φ του σχήματος, μεταξύ των διευθύνσεων εισόδου και εξόδου του ηλεκτρονίου.
δ) Ποια είναι η μεταβολή της ορμής του ηλεκτρονίου εξαιτίας της δύναμης Lorentz;
ε) Πόσο είναι το χρονικό διάστημα που διαρκεί η διέλευση του ηλεκτρονίου από το μαγνητικό πεδίο;






 Τυλίγουμε γύρω από ένα σωσίβιο (φουσκωμένο), μεταλλικό σύρμα, ψεκασμένο με μονωτικό βερνίκι, δημιουργώντας έτσι ένα πηνίο, αποτελούμενο από Ν σπείρες, που εφάπτονται μεταξύ τους.
Τυλίγουμε γύρω από ένα σωσίβιο (φουσκωμένο), μεταλλικό σύρμα, ψεκασμένο με μονωτικό βερνίκι, δημιουργώντας έτσι ένα πηνίο, αποτελούμενο από Ν σπείρες, που εφάπτονται μεταξύ τους.