Επαναληπτικό κατ/νσης Β – 2023
του Παντελή Παπαδάκη
Κατηγορία: 3.09 Επανάληψη
Επαναληπτική Άσκηση που φτιάξαμε στην τάξη Β2 με κάποια επιπλέον ερωτήματα…
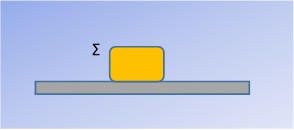Πάνω σε οριζόντιο επίπεδο ηρεμεί ένα μικρό σώμα Σ μάζας m = 2kg. Μεταξύ του σώματος και του δαπέδου οι συντελεστές στατικής τριβής και τριβής ολίσθησης είναι αντίστοιχα μσ = 0,5 και μ = 0,4.
Η βαρυτική επιτάχυνση είναι g = 10m/s2.
α) Ασκείται στο σώμα στατική τριβή; Δικαιολογείστε την απάντησή σας.
β) Αν ασκήσουμε οριζόντια προς τα δεξιά δύναμη μέτρου F1 = 6Ν, θα κινηθεί το σώμα; Δικαιολογείστε την απάντησή σας.
γ) Τη χρονική στιγμή t0 = 0, το σώμα βρίσκεται στη θέση x0 = 0 και ασκούμε οριζόντια προς τα δεξιά δύναμη μέτρου F2 = 16Ν.
γ1) Υπολογίστε το μέτρο της επιτάχυνσης του σώματος.
Επαναληπτικές Ασκήσεις – 2021
Πατήστε την εικόνα
Πηγές:
Ylikonet.gr
fysikafysikh.wordpress.com
Το παγκόσμιο ρεκόρ στον Άρη
Ο Ουκρανός Σεργκέι Μπούμπκα το 1994 έκανε παγκόσμιο ρεκόρ άλματος επί κοντώ στη Γη, με επίδοση hΓ = 6,14m. Μάλιστα το κράτησε μέχρι το 2020! Η αρχική ταχύτητα απογείωσης του Σεργκέι ήταν υ0 , το κέντρο βάρους του αθλητή βρισκόταν σε ύψος h1 = 1m από το έδαφος και όταν υπερπήδησε τον πήχη το κέντρο μάζας βρισκόταν σε ύψος h2 = 0,2m από αυτόν, έχοντας σχεδόν μηδενική ταχύτητα. Αν ο αγώνας γινόταν στον Άρη, με τα ίδια δεδομένα, εκτός από την μειωμένη βαρύτητα, υπολογίστε:
α) Την ένταση του πεδίου βαρύτητας στον Άρη.
β) Την επίδοση του αθλητή.
Το στέγνωμα των ρούχων
O τεχνικός ενός εργοστασίου που κατασκευάζει πλυντήρια, συμμετέχοντας σε σύσκεψη, για τις προδιαγραφές των συσκευών αυτών, παρουσίασε κάποιες μετρήσεις. Ο κυλινδρικός κάδος Κ ενός μοντέλου, ακτίνας R = 0,4m περιστρέφεται με τη βοήθεια ιμάντα, που διέρχεται από το αυλάκι μιας ομοαξονικής τροχαλίας Τ1 ακτίνας R1 = 0,2m, προσαρμοσμένης στο πίσω μέρος του κάδου. Ο ιμάντας τίθεται σε κίνηση αφού διέρχεται και από το αυλάκι δεύτερης τροχαλίας Τ2 ακτίνας R2 = 0,05m, η οποία κινείται με τη βοήθεια ηλεκτρικού κινητήρα.
α) Αν το πλυντήριο στύβει τα ρούχα στις 600στροφές /min, ο τεχνικός παρουσίασε ποια είναι η γωνιακή ταχύτητα και η αντίστοιχη συχνότητα περιστροφής, για την τροχαλία Τ2 του κινητήρα. Τι αποτελέσματα τους έδειξε;
β) Ένα στέλεχος του συμβουλίου τον ρώτησε «Γιατί τα ρούχα κολλάνε στην εσωτερική επιφάνεια του κάδου, καθώς αυτός περιστρέφεται; Πως αυτή η περιστροφή βοηθά το στέγνωμα;» Ο τεχνικός απάντησε τις ερωτήσεις και επιπλέον του είπε πόσα «G» δέχεται ένα ρούχο, εξαιτίας της γρήγορης περιστροφής και πόση δύναμη ασκεί ο κάδος σε ένα μικρό ρούχο μάζας m = 0,1kg, όταν βρίσκεται στην ανώτερη θέση κατά την περιστροφή του. Ποιες ήταν οι απαντήσεις;
γ) Ο τεχνικός παρουσίασε επίσης ότι, καθώς το στέγνωμα φτάνει στο τέλος του και η συχνότητα περιστροφής του κυλίνδρου μειώνεται, μια πλαστική σφαίρα αμελητέας ακτίνας, τοποθετημένη στον κάδο, χάνει την επαφή της, στη θέση που η επιβατική της ακτίνα σχηματίζει επίκεντρη γωνία θ = 600 με την κατακόρυφη. Έτσι μπόρεσε να υπολογίσει τη συχνότητα περιστροφής εκείνη ακριβώς τη στιγμή. Πόσο λέτε ότι βρήκε;
δ) Τέλος, για ένα μικρό ρούχο μάζας m = 0,1kg, παρουσίασε τη γραφική παράσταση της αλγεβρικής τιμής της κάθετης δύναμης στήριξης από τον κάδο, σε συνάρτηση με τη γωνία θ, που σχηματίζει η επιβατική ακτίνα με την κατακόρυφο, για την γωνιακή ταχύτητα του ερωτήματος (γ). Ποια ήταν η γραφική παράσταση περιστροφή του κάδου κατά π/3 rad;
Βάρος και βαρύτητα
Ένα σώμα μάζας m = 80kg βρίσκεται στον Ισημερινό και ισορροπεί ακίνητο ως προς το έδαφος. Η επιτάχυνση της βαρύτητας στην επιφάνεια της Γης είναι περίπου g = 10m/s2, η ακτίνα της Γης R = 6400km και η περίοδος περιστροφής της Γης Τ = 24h.
α) Ποιο είναι το μέτρο της γωνιακής και της γραμμικής ταχύτητας του σώματος εξαιτίας της περιστροφής της Γης γύρω από τον άξονά της;
β) Ποιο είναι το μέτρο της βαρυτικής έλξης από τη Γη στο σώμα; Είναι ίδιο με το μέτρο του «βάρους», που θα δείξει μια κλασσική ζυγαριά, αν την τοποθετήσουμε κάτω από το σώμα;
γ) Για ποια τιμή της περιόδου περιστροφής της Γης θα μπορούσε το σώμα να «πετάξει», λόγω έλλειψης βαρύτητας;
Απάντηση(Pdf)
Ο Σούπερμαν σώζει τη Λόις
Σε μια σκηνή του γνωστού κόμικ, ο Σούπερμαν μπαίνει μπροστά από την Λόις Λέιν, για να την σώσει από τις σφαίρες του Λεξ Λούθορ. Η καραμπίνα του Λεξ, περιέχει φυσίγγιο που ρίχνει N = 150 μικρά σφαιρίδια, μάζας m = 0,6g το καθένα και ταχύτητας μέτρου |υ1| = 600m/s. Τα σφαιρίδια χτυπούν ταυτόχρονα κάθετα στο στήθος του Σούπερμαν και ανακρούουν με ταχύτητα μέτρου |υ2| = 600m/s, αντίθετης φοράς από την αρχική.
Μια υπερπαραγωγή που θα ζήλευε και η Γ΄τάξη…
Πατήστε την εικόνα…
(Αφιερωμένη στον
Παντελεήμονα Παπαδάκη).
Από κατακόρυφη σε οριζόντια βολή
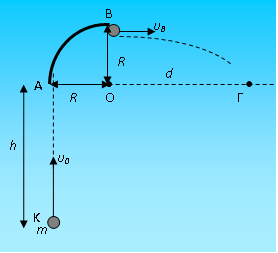Το σημειακό αντικείμενο του σχήματος έχει μάζα m = 0,5kg και εκτοξεύεται κατακόρυφα προς τα πάνω από το σημείο Κ. Αφού ανέλθει κατά h = 2m, εισέρχεται εφαπτομενικά στο λείο ακλόνητο τεταρτοκύκλιο κέντρου Ο και ακτίνας R = 1m και ολισθαίνει από το Α ως το Β.Αφού εγκαταλείψει το τεταρτοκύκλιο στο σημείο Β, με οριζόντια ταχύτητα υΒ περνάει από το σημείο Γ, που βρίσκεται στο ίδιο οριζόντιο επίπεδο με τα σημεία Ο και Α, όπου ΟΓ = d = 3m.
α) Ποια είναι η ταχύτητα υΒ του σώματος στο Β;
ΣΥΝΕΧΕΙΑ(pdf)
Ένας ποδηλάτης αλλάζει λάστιχο
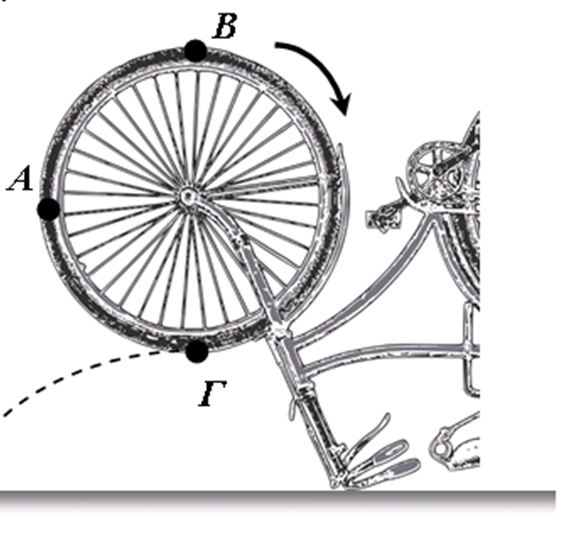Ένας ποδηλάτης προκειμένου να αλλάξει λάστιχο, γυρίζει ανάποδα το ποδήλατο και το σταθεροποιεί στο οριζόντιο έδαφος. Νωρίτερα είχε βρέξει και όταν γύρισε μια φορά και άφησε ελεύθερο τον τροχό, παρατήρησε σταγόνες νερού, που αποχωρίζονται όταν περνούν από την κατώτερη θέση, να φτάνουν στο έδαφος σε μέγιστη οριζόντια απόσταση x = 1,6m. H ακτίνα του τροχού είναι R = 0,5m και το κατώτερο σημείο του Γ απέχει από το οριζόντιο έδαφος h = 0,8m.
α) Μπορεί ο ποδηλάτης να υπολογίσει τη γωνιακή ταχύτητα του τροχού;
β) Με την ταχύτητα που υπολογίσατε στο (α) ερώτημα, πόσο διάστημα θα μπορούσε να διανύσει ο ποδηλάτης σε 10min;
γ) Ποιο είναι το μέτρο της ακτινικής συνιστώσας της δύναμης συνάφειας, που δέχεται από το λάστιχο μια σταγόνα μάζας m = 3.10-4kg, όταν περνά από:
i) το σημείο Α, που βρίσκεται στο ίδιο οριζόντιο επίπεδο με το κέντρο του τροχού;
ii) το ανώτερο σημείο Β;
iii) το κατώτερο σημείο Γ;
Δίνεται g = 10m/s2 και δεχόμαστε αμελητέες τριβές ή αντιστάσεις.
