Ο μεταλλικός κύλινδρος του σχήματος έχει την πάνω βάση του κλειστή και την κάτω ανοιχτή. Τον κρατάμε σε κατακόρυφη θέση, ώστε η κάτω βάση να εφάπτεται στην ήρεμη επιφάνεια του νερού μιας πισίνας. Το ύψος του κυλίνδρου είναι h = 1,1m και περιέχει αέρα που θεωρείται ιδανικό αέριο. Βυθίζουμε αργά όλο τον κύλινδρο στο νερό. Παρατηρούμε ότι μια ποσότητα νερού εισχωρεί μέχρι κάποιο ύψος εντός του κυλίνδρου και όταν επέλθει ισορροπία, ο εγκλωβισμένος αέρας γεμίζει μια κυλινδρική περιοχή σε βάθος y από την πάνω βάση.

α) Υπολογίστε την τιμή του y. Η μεταβολή θεωρείται ισόθερμη, η ατμοσφαιρική πίεση είναι p_atm = 10⁵N/m², η πυκνότητα του νερού ρ = 10 kg/m³ και η βαρυτική επιτάχυνση g = 10m/s².

β) Να κάνετε τη γραφική παράσταση p – V σε βαθμολογημένους άξονες,  αν η διάμετρος της βάσης του κυλίνδρου είναι δ = 0,8/√π m.

γ) Αν δίνεται ότι το πάχος του μετάλλου x = 5mm και η πυκνότητα του υλικού του ρ₁ = 2700kg/m³(αλουμίνιο), πόση δύναμη πρέπει να ασκηθεί για να κρατήσουμε τον κύλινδρο βυθισμένο;

δ) Στην ταινία “Πειρατές της Καραϊβικής” ο Τζακ Σπάροου βρίσκει τρόπο να γλυτώσει με την αντεστραμμένη βάρκα, που φαίνεται στην εικόνα, που όπως και στην περίπτωσή μας εγκλωβίζει αέρα και έτσι μπορούν να αναπνέουν κάτω από το νερό. Σχολιάστε τη σκηνή.

Απάντηση 

Απάντηση 

Α. Πηγές φωτός

Οι πιο κοινές πηγές φωτός είναι

α) Θερμαινόμενα στερεά, π.χ. νήμα από W(βολφράμιο) λυχνίας πυρακτώσεως.

β) Αέρια με τη βοήθεια ηλεκτρικής εκκένωσης, π.χ. λυχνία με Ne(Νέον).

γ) Φωτοδίοδοι (Light Emitting Diodes – LED), που αποτελούνται από ημιαγωγούς Ga, As, In κ.λ.π.

Το εκπεμπόμενο φως το αναλύουμε με ένα φασματόμετρο μετρώντας την φασματική αφετική ικανότητα Ι_λ, δηλαδή την ένταση της ακτινοβολίας ανά μονάδα μήκους κύματος.

Συνέχεια 

Συνέχεια 

Α. Από τη Θερμοδυναμική της Β΄τάξης ξέρουμε (;) ότι η μέση κινητική ενέργεια των μορίων ιδανικού αερίου είναι K_μ = (3/2) k_ΒΤ όπου k_B = 8,6∙10⁻⁵ eV/K η σταθερά του Boltzmann και Τ η απόλυτη θερμοκρασία του αερίου.

Σύμφωνα με την Κλασική Στατιστική Φυσική, τα άτομα των υλικών όταν ταλαντώνονται έχουν αντίστοιχα θερμική ενέργεια Ε_Θ = k_ΒΤ 

Υπολογίστε την ενέργεια αυτή σε eV για θερμοκρασία περιβάλλοντος Τ = 300Κ.

Β. Για έναν τυπικό μοριακό δεσμό, η σταθερά επαναφοράς του ταλαντωτή είναι της τάξης των δεκάδων ως εκατοντάδων N/m. Έστω δύο άτομα με:

• μικρό k₁ = 10N/m (μαλακό «ελατήριο)
• μεγάλο k₂ =1000N/m (σκληρό «ελατήριο»)

• Ας θεωρήσουμε πλάτος ταλάντωσης, 1Ångström (1A˚= 10⁻¹⁰ m).

Υπολογίστε σε eVτην ενέργεια ταλάντωσης κάθε ατόμου. Αν θεωρήσουμε μάζα για τα άτομα m = 10^-26kg, ποιες είναι οι αντίστοιχες συχνότητες ταλάντωσης; Δίνεται √10 = π.

Γ. Αν η σταθερά του Planck είναι h = 4,13∙10⁻¹⁵eV∙s, βρείτε το κβάντο ενέργειας κάθε ταλαντωτή.

Δ. Μπορείτε να εξηγήσετε τώρα σύμφωνα με την Κβαντική Φυσική, γιατί οι υψηλής συχνότητας ταλαντωτές σε θερμοκρασία περιβάλλοντος δεν ενεργοποιούνται;

Απάντηση 

Απάντηση 

Εργασία με την προσομοίωση «Φάσμα μελανού σώματος»

Ο σύνδεσμος της προσομοίωσης: ‪Φάσμα μελανού σώματος

Θα χρησιμοποιήσουμε την προσομοίωση, για να διερευνήσουμε πώς το φάσμα της ηλεκτρομαγνητικής ακτινοβολίας, που εκπέμπεται από ένα μέλαν σώμα, επηρεάζεται από τη θερμοκρασία του. Μπορούμε να παρατηρούμε την περιοχή του φάσματος της ηλεκτρομαγνητικής ακτινοβολίας  που εκπέμπει, το μήκος κύματος αιχμής και την αντίστοιχη ένταση ανά μονάδα μήκους κύματος (φασματική αφετική ικανότητα). Ταυτόχρονα βλέπουμε και συνολική ένταση (εμβαδόν καμπύλης), που εκπέμπεται σε όλα τα μήκη κύματος.

Ερωτήσεις 

α) Η θερμοκρασία των αστεριών στο σύμπαν ποικίλλει ανάλογα με τον τύπο του αστεριού και την ηλικία του. Εξετάζοντας τη μορφή του φάσματος του φωτός που εκπέμπεται από ένα αστέρι, μπορούμε να πούμε κάτι για τη μέση θερμοκρασία της επιφάνειάς του.
i) Αν παρατηρήσουμε το φάσμα ενός αστεριού και βρούμε ότι η μέγιστη ισχύς εμφανίζεται στο σύνορο μεταξύ κόκκινου και υπέρυθρου φωτός, ποια είναι κατά προσέγγιση η επιφανειακή θερμοκρασία του αστεριού;
ii) Αν παρατηρήσουμε το φάσμα ενός αστεριού και βρούμε ότι η μέγιστη ισχύς εμφανίζεται στο σύνορο μεταξύ μπλε και υπεριώδους φωτός, ποια είναι η επιφανειακή θερμοκρασία του αστεριού;
β) Οι λαμπτήρες λειτουργούν στους 2500K.
i) Ποιο είναι το μήκος κύματος στο οποίο εκπέμπεται η μεγαλύτερη ισχύς για έναν λαμπτήρα;
ii) Εξηγήστε γιατί οι λαμπτήρες πυρακτώσεως σπαταλούν πολλή ενέργεια.
γ) i) Διερευνήστε πώς το παρατηρούμενο φάσμα επηρεάζεται από τη μεταβολή της θερμοκρασίας.
iii) Σημειώστε τις σωστές ή λανθασμένες προτάσεις:
1. Αν μειώσετε τη θερμοκρασία ενός σώματος, η συνολική ποσότητα ισχύος που εκπέμπεται θα αυξηθεί σε ορισμένες περιπτώσεις.
2. Αν μειώσετε τη θερμοκρασία ενός σώματος, η συνολική ποσότητα ισχύος που εκπέμπεται μειώνεται σε όλες τις περιπτώσεις.
3. Αν αυξήσετε την επιφάνεια ενός σώματος, αλλά αφήσετε τη θερμοκρασία του αμετάβλητη, τότε το μεγαλύτερο μέρος της συνολικής του ισχύος θα εκπέμπεται ως ακτινοβολία υπερύθρων.
δ) Διερευνήσετε τις αλλαγές στην ποσότητα του εκπεμπόμενου φωτός στα ορατά μήκη κύματος, αλλάζοντας  τη θερμοκρασία από 2500K σε 2000K.
Ποια είναι κατά προσέγγιση η αναλογία μεταξύ της ισχύος που εκπέμπεται στα 500nm στους 2000K και της ισχύος στα 500nm στους 2500K;
ε) Ανεβάζετε τον επιλογέα ώστε η θερμοκρασία του νήματος να φτάσει τους 2600K. Το νήμα του λαμπτήρα έχει επιφάνεια S = 6,45∙10^-4 m² και ο συντελεστής θερμικής εκπομπής e = 0,8. Πόση ηλεκτρική ενέργεια πρέπει να καταναλώνει;
στ) Ο νόμος Wien δίνει τη σχέση μεταξύ της θερμοκρασίας Τ ενός μέλανος σώματος και του μήκους κύματος αιχμής λ_max.
i) Συμπληρώστε τον παρακάτω πίνακα:

Θερμοκρασία Τ (K)	Μήκος κύματος λmax (nm)	λmax ∙T(x 10-3 K∙m)
2000
3000
4000
5000
6000
10000
		Μέση τιμή:

ii) Επαληθεύεται ο νόμος Wien; Να κάνετε την αντίστοιχη γραφική παράσταση σε βαθμολογημένους άξονες.
ζ) Γιατί δε βλέπουμε τη θερμική ακτινοβολία των σωμάτων μέσα στο δωμάτιό μας;
η) Πόση ισχύ εκπέμπει ένας άνθρωπος;
θ) Στη διπλανή εικόνα φαίνεται μια ηλεκτρική εστία διαμέτρου 12cm, ισχύος 2500W.
Σε ποια θερμοκρασία θα φτάσει όταν το ανάψουμε; Τι χρώμα θα φαίνεται τότε;

Απάντηση 

Απάντηση 

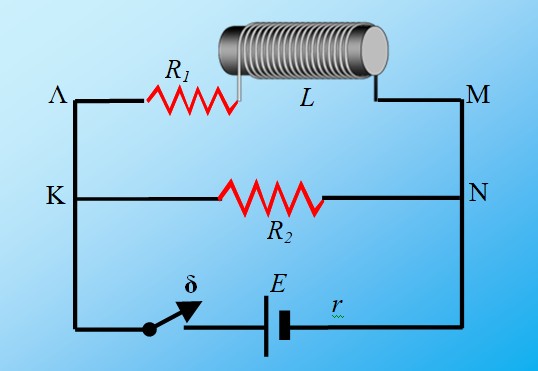Στο κύκλωμα του σχήματος δίνονται R₁ = 3Ω, R₂ = 6Ω, η πηγή ιδανική με ΗΕΔ Ε = 12V και το πηνίο ιδανικό με συντελεστή αυτεπαγωγής L = 0,3H.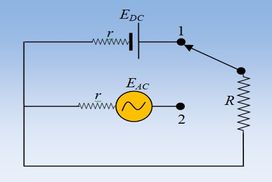

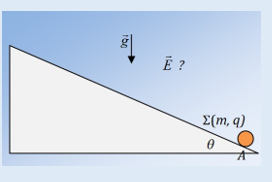i) Τη χρονική στιγμή t₀ = 0s κλείνουμε το διακόπτη δ και τον ανοίγουμε ακαριαία τη χρονική στιγμή t₁ = 1s. Δεδομένου ότι το χρονικό αυτό διάστημα είναι αρκετό για την αποκατάσταση του ρεύματος, βρείτε την ένταση του ρεύματος σε κάθε κλάδο του κυκλώματος και την αλγεβρική τιμή της ΗΕΔ αυτεπαγωγής στο πηνίο

α) τη χρονική στιγμή t = 0⁺s (ποσοτικά)

β) μια χρονική στιγμή 0s < t < 1s (ποιοτικά)

γ) τη χρονική στιγμή t = 1s (ποσοτικά)

ii) Μετά το άνοιγμα του διακόπτη και με δεδομένο ότι τη χρονική στιγμή t₂ = 2s έχει τελειώσει το φαινόμενο της αυτεπαγωγής, βρείτε την ένταση του ρεύματος σε κάθε κλάδο του κυκλώματος και την αλγεβρική τιμή της ΗΕΔ αυτεπαγωγής στο πηνίο

α) τη χρονική στιγμή t = 1⁺s (ποσοτικά)

β) Μια χρονική στιγμή 1s < t < 2s (ποιοτικά)

γ) τη χρονική στιγμή t = 2s (ποσοτικά)

iii) Να κάνετε τη γραφική παράσταση της έντασης του ρεύματος σε συνάρτηση με το χρόνο, που διαρρέει κάθε κλάδο του κυκλώματος πριν και μετά το άνοιγμα του διακόπτη.

iv) Να κάνετε τη γραφική παράσταση της ΗΕΔ αυτεπαγωγής στο πηνίο σε συνάρτηση με το χρόνο, πριν και μετά το άνοιγμα του διακόπτη.

v) Κάποια στιγμή t₁ όπου 0s < t₁ < 1s η ένταση του ρεύματος που δίνει η πηγή είναι i = 3A. Βρείτε τις ενεργειακές μετατροπές, υπολογίζοντας την ισχύ που ανταλλάσσει με το κύκλωμα κάθε δίπολο του κυκλώματος.

vi) Κάποια στιγμή t₁ όπου 1s < t₂ < 2s η ένταση του ρεύματος που διαρρέει το κύκλωμα είναι i₁ = 3A. Βρείτε τις ενεργειακές μετατροπές, υπολογίζοντας την ισχύ που ανταλλάσσει με το κύκλωμα κάθε δίπολο του κυκλώματος.

Απάντηση 

Απάντηση 

Η αντίσταση R = 3Ω, του διπλανού σχήματος βρίσκεται στο όριο υπερθέρμανσης και καταστροφής, όταν καταναλώνει ισχύ P = 27W. Με τον διακόπτη στη θέση 1, συνδέουμε την πηγή συνεχούς, που έχει εσωτερική αντίσταση r = 1Ω.

α) Ποια πρέπει να είναι η ΗΕΔ Ε_DC αυτής της πηγής;

Θέλουμε να μεταφέρουμε τον διακόπτη στη θέση 2, συνδέοντας πηγή εναλλασσόμενης τάσης, που προέρχεται από στρεφόμενο ορθογώνιο πλαίσιο, με διαστάσεις α = 30cm, β = 40cm, μέσα σε μαγνητικό πεδίο έντασης Β = 0,01Τ κάθετα στον άξονα περιστροφής του. Το πλαίσιο έχει Ν = 1000 σπείρες και στρέφεται με γωνιακή ταχύτητα ω = 10√2rad/s.

β) Κάποιος ισχυρίζεται ότι δεν πρέπει να το κάνουμε γιατί ο αντιστάτης θα λειώσει. Έχει δίκιο;

γ) Να γράψετε την εξίσωση i = f(t) του εναλλασσόμενου ρεύματος, που θα παρέχει αυτή η πηγή σε συνάρτηση με το χρόνο, αν την t₀ = 0s, i = 0A και το εμβαδικό διάνυσμα του πλαισίου είναι ομόρροπο με το διάνυσμα . Στη συνέχεια να την παραστήσετε γραφικά για μια περίοδο στο ίδιο σύστημα αξόνων με το αντίστοιχο ρεύμα I_DC, που παρέχει η πηγή συνεχούς.

δ) Ποιες χρονικές στιγμές στη διάρκεια της πρώτης ημιπεριόδου έχουμε i = I_AC; Σε τι ποσοστό του χρόνου μιας περιόδου αντιστοιχεί ο συνολικός χρόνος υπέρβασης του ορίου ρεύματος;

ε) Τι αλλαγές θα προτείνατε για την πηγή στρεφόμενου πλαισίου, ώστε να παρέχει την επιτρεπόμενη τάση στην αντίσταση;

στ) Αν υπολογίζαμε τη μέση ισχύ θα μπορούσαμε να εξετάσουμε αν κινδυνεύει να καταστραφεί ο αντιστάτης;

Απάντηση 

Απάντηση 

Ένα μικρό σώμα μάζας Σ, μάζας m = 0,3√3kg και φορτίου q = 5mC βρίσκεται ακίνητο σε σημείο Α λείου κεκλιμένου επιπέδου γωνίας θ =30°. Στο χώρο, εκτός από το (ομογενές) βαρυτικό πεδίο της Γης, μέτρου έντασης  g = 10Ν/kg, υπάρχει και οριζόντιο ομογενές ηλεκτρικό πεδίο έντασης Ε , άγνωστης φοράς.

α. Να υπολογίσετε την ένταση του ηλεκτρικού πεδίου (μέτρο και κατεύθυνση) ώστε το σώμα να παραμείνει ακίνητο.

Τριπλασιάζουμε το μέτρο της έντασης του ηλεκτρικού πεδίου, χωρίς να αλλάξουμε τη φορά της.

β. Υπολογίστε το μέτρο της επιτάχυνσης που αποκτά το σώμα κατά μήκος του κεκλιμένου επιπέδου.

γ. Με ποια ταχύτητα θα φτάσει το σώμα στο σημείο Β, που βρίσκεται σε ύψος h = 2,5m πάνω από το σημείο Α;

δ. Τη χρονική στιγμή που το σώμα διέρχεται από το σημείο Β βρείτε:

δ1. το ρυθμό μεταβολής κινητικής ενέργειας

δ2. το ρυθμό μεταβολής βαρυτικής δυναμικής ενέργειας

δ3. το ρυθμό μεταβολής ηλεκτρικής δυναμικής ενέργειας

και επαληθεύστε την Αρχή Διατήρησης της Μηχανικής Ενέργειας.

Απάντηση 

Απάντηση