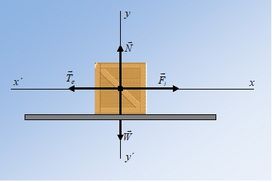
Σε οριζόντιο έδαφος ηρεμεί κιβώτιο μάζας m = 20kg, το οποίο παρουσιάζει με το έδαφος συντελεστή στατικής τριβής μσ = 0,5 και συντελεστή τριβής ολίσθησης μ = 0,4.
α) Ένας εργάτης, θέλοντας να το μετακινήσει, το σπρώχνει με οριζόντια δύναμη μέτρου F1 = 95N. Θα τα καταφέρει;
β) Αν αυξήσει το μέτρο της δύναμής του σε F2 = 140N ποια επιτάχυνση θα αποκτήσει το κιβώτιο;
γ) Αν θεωρήσουμε τη χρονική στιγμή, που ασκήθηκε η δύναμη, ως t0 = 0s και το κιβώτιο να βρίσκεται στη θέση x0 = 0m ενός άξονα x΄x, βρείτε τη χρονική t1 = 4s, ποια θα είναι η θέση του x1, το μέτρο υ1 της ταχύτητας και η κινητική ενέργειά του Κ1.
δ) Ποιες ενεργειακές μετατροπές συνέβησαν κατά τη διάρκεια της μετατόπισης του κιβωτίου;
ε) Να βρείτε τη χρονική εξίσωση PF2 = f(t) της στιγμιαίας ισχύος, που παρέχει ο εργάτης στο κιβώτιο ασκώντας τη δύναμη και να γίνει η γραφική της παράσταση από 0 ως 4s. Τι εκφράζει το εμβαδόν κάτω από τη γραφική παράσταση;
στ) Υπολογίστε τη στιγμιαία ισχύ κάθε δύναμης, που παράγει έργο, τη χρονική στιγμή t1 = 4s και τη μέση ισχύ κάθε δύναμης που παράγει έργο από 0 ως 4s. Επαληθεύεται η Αρχή Διατήρησης της Ενέργειας;
ζ) Αν τη χρονική στιγμή t1 = 4s καταργηθεί η δύναμη , ποια χρονική στιγμή t2 και σε ποια θέση x2 του άξονα x΄x θα σταματήσει το κιβώτιο;
η) Να κάνετε τις γραφικές παραστάσεις x = f(t) της θέσης και υ = f(t) της ταχύτητας του κιβωτίου για ολόκληρη την κίνηση.
Η επιτάχυνση της βαρύτητας έχει μέτρο g = 10 m/s2 και δεν υπάρχει αντίσταση από τον αέρα.



