Πατήστε το τραίνο
Μήνας: Απρίλιος 2024
Επανάληψη Φυσικής Α΄ 2024
Ένας γρήγορος ανελκυστήρας

Ο ανελκυστήρας, που βρίσκεται στον ουρανοξύστη Taipei 101 της Ταϊβάν, είναι πολύ γρήγορος. Όπως μπορείτε να δείτε στο βίντεο The Taipei 101 elevator, fastest in the world,
ανεβαίνει από τον 5ο στον 89ο όροφο, μέσα σε 37s! Ξεκινάει από την ηρεμία, επιταχύνεται ομαλά πιάνοντας την τελική του ταχύτητα υ1 = 1010 m/min, μέσα σε 14s, κινείται ομαλά μέχρι τα 21s και στη συνέχεια επιβραδύνεται ομαλά. Διαθέτει κατάλληλα αντίβαρα που εξισορροπούν το βάρος του θαλάμου του ανελκυστήρα, οπότε ο κινητήρας δεν χρειάζεται να σηκώνει και το θάλαμο… Η μέγιστη ισχύς του κινητήρα είναι Pmax = 330 kW.
α) Να κάνετε τα διαγράμματα επιτάχυνσης – χρόνου, ταχύτητας – χρόνου και μετατόπισης – χρόνου, σε άξονες βαθμολογημένους στο S.I.
β) Σε ποια φάση απαιτείται το μέτρο της δύναμης που ασκεί ο κινητήρας να είναι μέγιστο;
γ) Ποια στιγμή θα απαιτηθεί η μέγιστη ισχύς από τον κινητήρα;
δ) Ποιος είναι ο μέγιστος αριθμός επιβατών μάζας m = 70kg που μπορεί να μεταφέρει ο ανελκυστήρας;
Θεωρούμε g = 10m/s2. Οι αριθμοί πάρθηκαν κατά προσέγγιση με παρατήρηση του ερασιτεχνικού βίντεο.
Το γραμμικό φάσμα εκπομπής του Υδρογόνου και ο Bohr

Ποιο είδος φάσματος παρατηρούμε; Προσδιορίστε τα μήκη κύματος και τις συχνότητες, των τεσσάρων φασματικών γραμμών, που είναι ορατές. Δίνεται η ταχύτητα του φωτός στο κενό
c = 3∙108m/s και η σταθερά του Planck h = 6,63∙10-34Js.
β) Τι εξήγηση έδωσε ο Bohr για αυτό το φάσμα;
γ) Υπολογίστε τις 3 πρώτες διεγερμένες ενεργειακές στάθμες του ατόμου του Η σε eV, καθώς και την μέγιστη ενέργεια, που θα μπορούσε να έχει το ηλεκτρόνιο. Σχεδιάστε το διάγραμμα των ενεργειακών σταθμών που υπολογίσατε, σε βαθμολογημένο άξονα.
δ) Υπολογίστε την ενέργεια διέγερσης του ηλεκτρονίου για μετάβαση από
Ε1→Ε2, Ε1→Ε3, Ε1→Ε4, Ε1→Ε∞(ενέργεια ιονισμού).
ε) Αν τα ιόντα-βλήματα μέσα στη λυχνία υδρογόνου έχουν κινητική ενέργεια Κβλ(αρχ), που φαίνεται στον παρακάτω πίνακα, κάποια από αυτά μπορούν να διεγείρουν άτομα υδρογόνου.
Συμπληρώστε τις υπόλοιπες στήλες του πίνακα, εξηγώντας πως προέκυψαν. Υποθέτουμε ότι σε κάθε άτομο Η, το ηλεκτρόνιο βρίσκεται αρχικά στη θεμελιώδη ενεργειακή του στάθμη.
| Κβλ(αρχ)(eV) | Σύγκριση Κβλ(αρχ) – Εδ | Εf (eV) | Κβλ(τελ)(eV) |
| 9,59 | |||
| 11,2 | |||
| 12,5 | |||
| 12,75 | |||
| 13,6 |
στ) Αφού παραμείνει για 10-8s σε διεγερμένη στάθμη, το ηλεκτρόνιο επιστρέφει στη θεμελιώδη του Ε1. Υπολογίστε τα μήκη κύματος των πιθανών φωτονίων, που μπορεί να εκπέμψει και σχεδιάστε στο διάγραμμα ενεργειακών σταθμών τις αντίστοιχες μεταβάσεις.
Δίνεται ότι hc = 1243eV∙nm.
Λαμπάκια LED και φωτοηλεκτρικό φαινόμενο

| Πηγή LED -Χρώμα | λ(nm) |
| Ερυθρό | 620 |
| Πορτοκαλί | 586 |
| Πράσινο | 530 |
| Μπλε | 485 |
Εκτελούμε το πείραμα παρατήρησης φωτοηλεκτρικού φαινομένου στο εργαστήριο, χρησιμοποιώντας ως φωτεινή πηγή μονοχρωματικού φωτός λάμπες LED, οι οποίες εκπέμπουν μήκη κύματος, που φαίνονται στον παραπάνω πίνακα.
Η φωτοκάθοδος της συσκευής είναι από Cs (καίσιο), που έχει έργο εξαγωγής
φ = 2,87 ∙ 10-19J.
α) Θεωρώντας γνωστή τη σχέση Εph = 1242(eV∙nm) / λ(nm), εξετάστε ποιες από τις λάμπες μπορούν να χρησιμοποιηθούν για την εξαγωγή φωτοηλεκτρονίων.
β) Χρησιμοποιώντας τις λάμπες που βρήκατε στο ερώτημα (α) συμπληρώστε τον παρακάτω πίνακα:
| Πηγή Led -Χρώμα | λ(nm) | f(*1014Hz) | Εph (eV) | Kmax (eV) | V0 (V) |
Δίνεται η ταχύτητα φωτός στο κενό ή αέρα c = 3∙108m/s.
γ) Να κάνετε τη γραφική παράσταση Kmax → f σε βαθμολογημένους άξονες, θεωρώντας ότι είναι ευθεία. Με τη βοήθεια της γραφικής παράστασης υπολογίστε τη σταθερά του Planck και το σχετικό σφάλμα μέτρησης, αν η τιμή της σταθεράς είναι h = 6,63∙10-34Js.
δ) Χρησιμοποιώντας τη μπλε λάμπα, πλησιάζουμε τη φωτεινή πηγή στη μισή απόσταση (από d σε d/2), σε σχέση με αυτή που βρισκόταν ως τώρα.
δ1) Τι θα συμβεί με τη φωτονική ροή πάνω στην κάθοδο;
δ2) Να κάνετε ποιοτική γραφική παράσταση της έντασης του φωτορεύματος i σε συνάρτηση με την τάση VAK (ανόδου – καθόδου), πριν και μετά το πλησίασμα της φωτεινής πηγής. Υποθέτουμε ότι κάθε φωτόνιο εξάγει ένα ηλεκτρόνιο.
ε) Να κάνετε ποιοτική γραφική παράσταση της έντασης του φωτορεύματος i σε συνάρτηση με την τάση VAK (ανόδου – καθόδου), για την κόκκινη και τη μπλε λάμπα τοποθετημένες στην ίδια απόσταση από τη φωτοκάθοδο. Υποθέτουμε ότι κάθε φωτόνιο εξάγει ένα ηλεκτρόνιο.
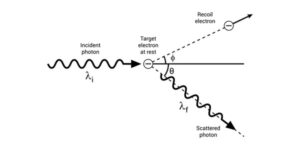
Στοιχεία Ειδικής Θεωρίας Σχετικότητας και Φαινόμενο Compton
Η χιονισμένη σανίδα

Μια χειμωνιάτικη μέρα, ένας εργάτης εκτοξεύει τούβλα …προς τα πάνω, από τη βάση μιας κεκλιμένης σανίδας, με γωνία κλίσης θ = 300. Η σανίδα έχει πιάσει πάγο όχι ομοιόμορφα, έχοντας παγώσει περισσότερο στο κάτω μέρος. Σαν συνέπεια, ο συντελεστής τριβής ολίσθησης αυξάνεται με την απόσταση από τη βάση της σανίδας και δίνεται από την εξίσωση μ = c∙x, όπου c = (1/2√3)m-1 μια θετική σταθερά και x η απόσταση που διανύει κάθε τούβλο πάνω στη σανίδα με x = 0 στο έδαφος. Οι συντελεστές τριβής στατικής και ολισθήσεως θεωρούνται ίσοι. Ο εργάτης δίνει στα τούβλα αρχική ταχύτητα μέτρου υ0 και η βαρυτική επιτάχυνση είναι g = 10m/s2. Δίνονται και ημ30 = ½, συν30 = √3/2.
α) Αν η αρχική ταχύτητα είναι σχετικά μικρή, ο εργάτης παρατηρεί ότι το κάθε τούβλο ανέρχεται στη σανίδα, σταματάει και επιστρέφει. Από μια κρίσιμη όμως τιμή και πάνω, στο μέτρο της αρχικής ταχύτητας, τα τούβλα φτάνουν σε κάποιο σημείο σταματούν και δεν επιστρέφουν. Μπορείτε να δώσετε μια ποιοτική εξήγηση για αυτό το φαινόμενο;
β) Ποια είναι η ελάχιστη απόσταση xmin, που πρέπει να διανύσει ένα τούβλο πάνω στη σανίδα, για να σταματήσει μόνιμα; Η απόσταση αυτή εξαρτάται από τη μάζα των τούβλων;
γ) Βρείτε το μέτρο Τ της τριβής ολίσθησης, σε συνάρτηση με τη μάζα M κάθε τούβλου και την απόσταση x από το σημείο εκτόξευσης και κάνετε την αντίστοιχη γραφική παράσταση μέχρι τη θέση xmin, που υπολογίσατε στο ερώτημα (β).
δ) Βρείτε το μέτρο της αρχικής ταχύτητας υ0, που απαιτείται για να φτάνει κάθε τούβλο στη θέση xmin.
Δυο έμβολα κινούνται παρέα
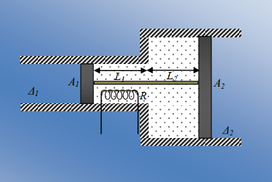 Τα τοιχώματα των δύο ενωμένων κυλινδρικών δοχείων Δ1, Δ2 του σχήματος είναι αδιαβατικά (θερμομονωτικά). Οι εγκάρσιες διατομές των κυλίνδρων είναι Α1 =1∙10-1m2, A2 = 4∙10-1m2 αντίστοιχα. Σε κάθε δοχείο υπάρχει από ένα έμβολο καλά εφαπτόμενο στα τοιχώματα, αλλά ελεύθερα κινούμενο, χωρίς τριβές, σε αποστάσεις L1 = L2 = L = 1,5∙10-1m από το σημείο που αλλάζει η εγκάρσια διατομή. Τα έμβολα συνδέονται μεταξύ τους με πολύ λεπτή αβαρή ράβδο. Στον κλειστό χώρο που δημιουργείται, ανάμεσα στα έμβολα, υπάρχει ιδανικό αέριο σε θερμοκρασία Τ0 = 300Κ. Η πίεση του αερίου είναι ίση με την εξωτερική ατμοσφαιρική δηλαδή p0 = patm = 105Pa.
Τα τοιχώματα των δύο ενωμένων κυλινδρικών δοχείων Δ1, Δ2 του σχήματος είναι αδιαβατικά (θερμομονωτικά). Οι εγκάρσιες διατομές των κυλίνδρων είναι Α1 =1∙10-1m2, A2 = 4∙10-1m2 αντίστοιχα. Σε κάθε δοχείο υπάρχει από ένα έμβολο καλά εφαπτόμενο στα τοιχώματα, αλλά ελεύθερα κινούμενο, χωρίς τριβές, σε αποστάσεις L1 = L2 = L = 1,5∙10-1m από το σημείο που αλλάζει η εγκάρσια διατομή. Τα έμβολα συνδέονται μεταξύ τους με πολύ λεπτή αβαρή ράβδο. Στον κλειστό χώρο που δημιουργείται, ανάμεσα στα έμβολα, υπάρχει ιδανικό αέριο σε θερμοκρασία Τ0 = 300Κ. Η πίεση του αερίου είναι ίση με την εξωτερική ατμοσφαιρική δηλαδή p0 = patm = 105Pa.
α) Ποιο είναι το μέτρο της δύναμης, που ασκεί σε κάθε έμβολο η ράβδος σύνδεσης, στην αρχική κατάσταση ισορροπίας;
Αφήνουμε για χρονικό διάστημα Δt = 2min, να διέλθει ηλεκτρικό ρεύμα από τον αντιστάτη R, ο οποίος έχει ισχύ P = 30W.
β) Ποιο είναι το είδος της μεταβολής που υφίσταται το αέριο;
γ) Σε ποια κατεύθυνση θα μετακινηθούν τα έμβολα και γιατί;
δ) Ποια θα είναι η μετατόπιση των εμβόλων, μέχρι η νέα κατάσταση ισορροπίας να πραγματοποιηθεί;
ε) Ποια θα είναι η τελική θερμοκρασία του αερίου;