Μια ομογενής λεπτή ράβδος ΑΒ με μήκος L = 2m, τη χρονική στιγμή t0 = 0s, έχει τη διεύθυνση του άξονα Οx, ενός συστήματος xOy ορθογωνίων αξόνων, με το μέσον – και κέντρο μάζας – C, να συμπίπτει με την αρχή Ο των αξόνων.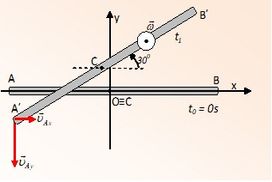
Κάποια χρονική στιγμή t1 βρίσκεται για πρώτη φορά στη θέση του διπλανού σχήματος, έχοντας στραφεί αντιωρολογιακά κατά Δθ = 300.
Οι συνιστώσες της ταχύτητας του άκρου Α, έχουν αλγεβρικές τιμές υΑx =+ 2m/s και υAy = -6m/s για κάθε άξονα, ενώ η γωνιακή ταχύτητα της ράβδου έχει σταθερό μέτρο ω = 12rad/s, με αντιωρολογιακή φορά.
Θεωρείστε την κίνηση της ράβδου σύνθετη: Ομαλή Στροφική, γύρω από άξονα κάθετο στο επίπεδο xOy που διέρχεται από το κέντρο μάζας C της ράβδου και ευθύγραμμη ομαλή μεταφορική με την ταχύτητα του κέντρου μάζας C. Για τη χρονική στιγμή t1:
α) Υπολογίστε την ταχύτητα του κέντρου μάζας.
β) Υπολογίστε την ταχύτητα του άκρου Β.
γ) Υπολογίστε τη χρονική στιγμή t1 και βρείτε τη θέση του σημείου Α ως προς το δοσμένο σύστημα αξόνων.
