και η Απάντησή της
ΑΣΚΗΣΕΙΣ ΦΥΣΙΚΗΣ και όχι μόνο…
Ανδρέας Ριζόπουλος – Καθηγητής Φυσικής 12ου Λυκείου Πατρών
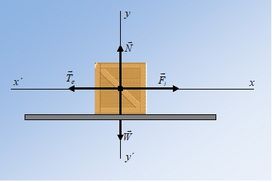
Σε οριζόντιο έδαφος ηρεμεί κιβώτιο μάζας m = 20kg, το οποίο παρουσιάζει με το έδαφος συντελεστή στατικής τριβής μσ = 0,5 και συντελεστή τριβής ολίσθησης μ = 0,4.
α) Ένας εργάτης, θέλοντας να το μετακινήσει, το σπρώχνει με οριζόντια δύναμη μέτρου F1 = 95N. Θα τα καταφέρει;
β) Αν αυξήσει το μέτρο της δύναμής του σε F2 = 140N ποια επιτάχυνση θα αποκτήσει το κιβώτιο;
γ) Αν θεωρήσουμε τη χρονική στιγμή, που ασκήθηκε η δύναμη, ως t0 = 0s και το κιβώτιο να βρίσκεται στη θέση x0 = 0m ενός άξονα x΄x, βρείτε τη χρονική t1 = 4s, ποια θα είναι η θέση του x1, το μέτρο υ1 της ταχύτητας και η κινητική ενέργειά του Κ1.
δ) Ποιες ενεργειακές μετατροπές συνέβησαν κατά τη διάρκεια της μετατόπισης του κιβωτίου;
ε) Να βρείτε τη χρονική εξίσωση PF2 = f(t) της στιγμιαίας ισχύος, που παρέχει ο εργάτης στο κιβώτιο ασκώντας τη δύναμη και να γίνει η γραφική της παράσταση από 0 ως 4s. Τι εκφράζει το εμβαδόν κάτω από τη γραφική παράσταση;
στ) Υπολογίστε τη στιγμιαία ισχύ κάθε δύναμης, που παράγει έργο, τη χρονική στιγμή t1 = 4s και τη μέση ισχύ κάθε δύναμης που παράγει έργο από 0 ως 4s. Επαληθεύεται η Αρχή Διατήρησης της Ενέργειας;
ζ) Αν τη χρονική στιγμή t1 = 4s καταργηθεί η δύναμη , ποια χρονική στιγμή t2 και σε ποια θέση x2 του άξονα x΄x θα σταματήσει το κιβώτιο;
η) Να κάνετε τις γραφικές παραστάσεις x = f(t) της θέσης και υ = f(t) της ταχύτητας του κιβωτίου για ολόκληρη την κίνηση.
Η επιτάχυνση της βαρύτητας έχει μέτρο g = 10 m/s2 και δεν υπάρχει αντίσταση από τον αέρα.
 Ιδανικό αέριο υποβάλλεται στην κυκλική μεταβολή ΑΒΓΔΕΖΓΗΑ του σχήματος. Οι δύο καμπύλες έχουν σχήμα κύκλου με ακτίνες R1 > R2.
Ιδανικό αέριο υποβάλλεται στην κυκλική μεταβολή ΑΒΓΔΕΖΓΗΑ του σχήματος. Οι δύο καμπύλες έχουν σχήμα κύκλου με ακτίνες R1 > R2.
i) Κατά τη διάρκεια της πλήρους κυκλικής μεταβολής το αέριο παράγει
α) Θετικό έργο β) Αρνητικό έργο γ) Μηδενικό έργο
Βρείτε τη σωστή απάντηση και δικαιολογείστε την.
ii) Στην κυκλική αυτή μεταβολή η συνολική θερμότητα, που ανταλλάσσει το αέριο εισρέει ή αποβάλλεται από το σύστημα; Εξηγείστε.
iii) Θα μπορούσε να χρησιμοποιηθεί αυτός ο κύκλος από μια θερμική μηχανή; Εξηγείστε.
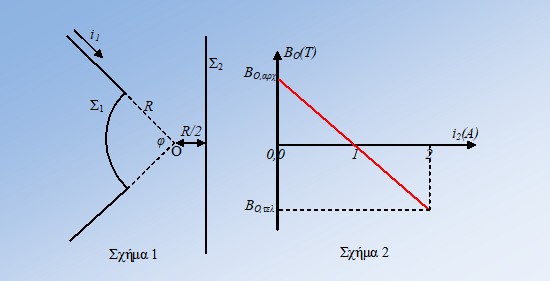
α) Χωρίς να κάνετε αριθμητικές πράξεις δώστε την εξίσωση υπολογισμού του μέτρου Β1 της έντασης του μαγνητικού πεδίου, που δημιουργεί ο αγωγός Σ1 στο σημείο Ο.
β) Δικαιολογείστε ποια είναι η φορά του ρεύματος i2.
γ) Υπολογίστε την επίκεντρη γωνία φ του κυκλικού τόξου.
δ) Αν δίνονται R = 0,02m, μ0/4π = 10-7Ν/Α2, γράψτε την εξίσωση της ευθείας του σχήματος 2 και υπολογίστε τις τιμές ΒΟ,αρχ και ΒΟ,τελ.

Μια θερμική μηχανή Carnot C1, προσλαμβάνει θερμότητα από μια δεξαμενή θερμοκρασίας θh1 = 7270C με ρυθμό Ph1 = 6kW και αποβάλλει θερμότητα στο περιβάλλον, που έχει θερμοκρασία Τc1 = 300K. Η μηχανική ισχύς που παράγει η θερμική μηχανή χρησιμοποιείται για να τροφοδοτήσει ένα ψυγείο Carnot C2 . Τι κάνει το ψυγείο; Αφαιρεί θερμότητα από το χώρο ψύξης ο οποίος έχει έτσι θερμοκρασία θc2 = -130C και την αποβάλλει στο περιβάλλον που έχει θερμοκρασία Τh2 = 300K. Αφού σχεδιάσετε τις δυο μηχανές, υπολογίστε:
α) Την απόδοση της θερμικής μηχανής C1 και τη μηχανική ισχύ P1, που προσφέρει στο ψυγείο.
β) Ποιος είναι ο συντελεστής λειτουργίας του ψυγείου C2.
γ) Το ρυθμό με τον οποίο αφαιρείται θερμότητα από το χώρο ψύξης στην C2.
δ) Το ρυθμό με τον οποίο αποβάλλεται θερμότητα στο περιβάλλον από το ψυγείο C2.
ε) Το συνολικό ρυθμό αποβολής θερμότητας στο περιβάλλον του συστήματος των δυο μηχανών.
Μια ομογενής λεπτή ράβδος ΑΒ με μήκος L = 2m, τη χρονική στιγμή t0 = 0s, έχει τη διεύθυνση του άξονα Οx, ενός συστήματος xOy ορθογωνίων αξόνων, με το μέσον – και κέντρο μάζας – C, να συμπίπτει με την αρχή Ο των αξόνων.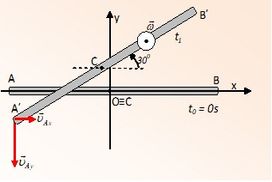 Κάποια χρονική στιγμή t1 βρίσκεται για πρώτη φορά στη θέση του διπλανού σχήματος, έχοντας στραφεί αντιωρολογιακά κατά Δθ = 300.
Κάποια χρονική στιγμή t1 βρίσκεται για πρώτη φορά στη θέση του διπλανού σχήματος, έχοντας στραφεί αντιωρολογιακά κατά Δθ = 300.
Οι συνιστώσες της ταχύτητας του άκρου Α, έχουν αλγεβρικές τιμές υΑx =+ 2m/s και υAy = -6m/s για κάθε άξονα, ενώ η γωνιακή ταχύτητα της ράβδου έχει σταθερό μέτρο ω = 12rad/s, με αντιωρολογιακή φορά.
Θεωρείστε την κίνηση της ράβδου σύνθετη: Ομαλή Στροφική, γύρω από άξονα κάθετο στο επίπεδο xOy που διέρχεται από το κέντρο μάζας C της ράβδου και ευθύγραμμη ομαλή μεταφορική με την ταχύτητα του κέντρου μάζας C. Για τη χρονική στιγμή t1:
α) Υπολογίστε την ταχύτητα του κέντρου μάζας.
β) Υπολογίστε την ταχύτητα του άκρου Β.
γ) Υπολογίστε τη χρονική στιγμή t1 και βρείτε τη θέση του σημείου Α ως προς το δοσμένο σύστημα αξόνων.
