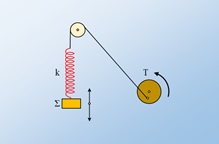
O τεχνικός ενός εργοστασίου που κατασκευάζει πλυντήρια, συμμετέχοντας σε σύσκεψη, για τις προδιαγραφές των συσκευών αυτών, παρουσίασε κάποιες μετρήσεις. Ο κυλινδρικός κάδος Κ ενός μοντέλου, ακτίνας R = 0,4m περιστρέφεται με τη βοήθεια ιμάντα, που διέρχεται από το αυλάκι μιας ομοαξονικής τροχαλίας Τ1 ακτίνας R1 = 0,2m, προσαρμοσμένης στο πίσω μέρος του κάδου. Ο ιμάντας τίθεται σε κίνηση αφού διέρχεται και από το αυλάκι δεύτερης τροχαλίας Τ2 ακτίνας R2 = 0,05m, η οποία κινείται με τη βοήθεια ηλεκτρικού κινητήρα.
α) Αν το πλυντήριο στύβει τα ρούχα στις 600στροφές /min, ο τεχνικός παρουσίασε ποια είναι η γωνιακή ταχύτητα και η αντίστοιχη συχνότητα περιστροφής, για την τροχαλία Τ2 του κινητήρα. Τι αποτελέσματα τους έδειξε;
β) Ένα στέλεχος του συμβουλίου τον ρώτησε «Γιατί τα ρούχα κολλάνε στην εσωτερική επιφάνεια του κάδου, καθώς αυτός περιστρέφεται; Πως αυτή η περιστροφή βοηθά το στέγνωμα;» Ο τεχνικός απάντησε τις ερωτήσεις και επιπλέον του είπε πόσα «G» δέχεται ένα ρούχο, εξαιτίας της γρήγορης περιστροφής και πόση δύναμη ασκεί ο κάδος σε ένα μικρό ρούχο μάζας m = 0,1kg, όταν βρίσκεται στην ανώτερη θέση κατά την περιστροφή του. Ποιες ήταν οι απαντήσεις;
γ) Ο τεχνικός παρουσίασε επίσης ότι, καθώς το στέγνωμα φτάνει στο τέλος του και η συχνότητα περιστροφής του κυλίνδρου μειώνεται, μια πλαστική σφαίρα αμελητέας ακτίνας, τοποθετημένη στον κάδο, χάνει την επαφή της, στη θέση που η επιβατική της ακτίνα σχηματίζει επίκεντρη γωνία θ = 600 με την κατακόρυφη. Έτσι μπόρεσε να υπολογίσει τη συχνότητα περιστροφής εκείνη ακριβώς τη στιγμή. Πόσο λέτε ότι βρήκε;
δ) Τέλος, για ένα μικρό ρούχο μάζας m = 0,1kg, παρουσίασε τη γραφική παράσταση της αλγεβρικής τιμής της κάθετης δύναμης στήριξης από τον κάδο, σε συνάρτηση με τη γωνία θ, που σχηματίζει η επιβατική ακτίνα με την κατακόρυφο, για την γωνιακή ταχύτητα του ερωτήματος (γ). Ποια ήταν η γραφική παράσταση περιστροφή του κάδου κατά π/3 rad;
Απάντηση(Pdf)