Θέματα & Λύσεις

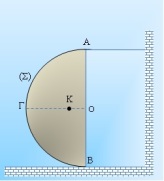Κόβουμε ένα δίσκο μικρού πάχους, ακτίνας R = 1m κατά μήκος μιας διαμέτρου του ΑΒ. Παίρνουμε το ένα κομμάτι (Σ), μάζας Μ = 2kg και το στερεώνουμε, όπως στο σχήμα, με αβαρές νήμα, έτσι ώστε η διάμετρος ΑΒ να είναι κατακόρυφη. Αν γνωρίζουμε ότι το κέντρο μάζας του ημιδισκίου Σ, βρίσκεται πάνω στην οριζόντια ακτίνα ΟΓ, στο σημείο Κ, με  ΟΚ = d = 4R/3π, g = 10m/s² και η ροπή αδράνειας ομογενούς δίσκου ως προς άξονα κάθετο στο επίπεδό του που διέρχεται από το κέντρο του είναι Ι_δ(Ο) = 1/2 Μ_δR²

α) Σχεδιάστε τις δυνάμεις και υπολογίστε την τάση του νήματος.

β) Βρείτε τη δύναμη που ασκείται από το οριζόντιο επίπεδο, στο σημείο Β του ημιδισκίου.

γ) Ποια είναι η ελάχιστη τιμή του συντελεστή στατικής τριβής, που πρέπει να έχει το ημιδίσκιο Σ με το δάπεδο ώστε να μην ολισθαίνει;

Αν κόψουμε το νήμα παρατηρούμε ότι το ημιδίσκιο ξεκινά να κυλίεται χωρίς ολίσθηση, με το επίπεδό του να παραμένει κατακόρυφο.

δ) Ποια είναι η ροπή αδράνειάς του ως προς άξονα κάθετο στο επίπεδό του που διέρχεται από το κέντρο μάζας του Κ;

ε) Ποια θα είναι η γωνιακή ταχύτητα του ημιδισκίου τη στιγμή που η διάμετρος ΑΒ γίνεται για πρώτη φορά οριζόντια;

στ) Ποια θα είναι τότε η στροφορμή του ημιδισκίου, ως προς τον οριζόντια άξονα που διέρχεται από το κέντρο του Ο;

Απάντηση(Pdf)

Ένα συρμάτινο πλαίσιο έχει σχήμα ημικυκλίου, ακτίνας r = 1m, με αντίσταση ανά μονάδα μήκους R^* = 0,5Ω/m. Με όριο τη διάμετρο ΑΓ, όπως φαίνεται στο σχήμα, υπάρχει ομογενές μαγνητικό πεδίο με την ένταση να είναι κάθετη στο επίπεδο του πλαισίου, έχοντας μέτρο Β = 1Τ. Το πλαίσιο τη χρονική στιγμή t = 0, αρχίζει να στρέφεται με σταθερή γωνιακή ταχύτητα μέτρου ω =10,28rad/s κατά την αντιωρολογιακή φορά, γύρω από άξονα κάθετο στο επίπεδό του, που διέρχεται από το κέντρο Ο. Θεωρούμε το εμβαδικό διάνυσμα n της επιφάνειας του πλαισίου, ομόρροπο του Β.

α) Να εξηγήσετε γιατί το πλαίσιο διαρρέεται από ρεύμα.

β) Να βρείτε σε κάθε περίοδο περιστροφής του πλαισίου τη χρονική εξέλιξη της αλγεβρικής τιμής της μαγνητικής ροής, που διέρχεται από την επιφάνεια του πλαισίου. Στη συνέχεια να κάνετε τη γραφική παράσταση της αλγεβρικής τιμής της μαγνητικής ροής σε συνάρτηση με το χρόνο, σε βαθμολογημένους άξονες, για δύο περιόδους περιστροφής.

γ) Να βρείτε σε κάθε περίοδο περιστροφής του πλαισίου τη χρονική εξέλιξη της αλγεβρικής τιμής της έντασης του επαγωγικού ρεύματος. Στη συνέχεια να κάνετε τη γραφική παράσταση της αλγεβρικής τιμής της έντασης του επαγωγικού ρεύματος σε συνάρτηση με το χρόνο, σε βαθμολογημένους άξονες, για δύο περιόδους περιστροφής και να σχεδιάσετε στο σχήμα τη φορά της στη διάμετρο ΑΓ.

δ) Το επαγωγικό ρεύμα, που διαρρέει το πλαίσιο, θα το χαρακτηρίζατε συνεχές ή εναλλασσόμενο;
Αν είναι εναλλασσόμενο θα μπορούσατε να βρείτε την ενεργό ένταση και τη θερμική ενέργεια που αναπτύσσεται στο πλαίσιο σε χρονικό διάστημα μιας περιόδου;

Απάντηση(Word)

Απάντηση(Pdf)

Για να δείτε τη μετάλλαξη των ερωτήσεων 301-400 πατήστε ΕΔΩ

Και για την μετάλλαξη των απαντήσεων 301-400 πατήστε ΕΔΩ

Οι υπόλοιπες μεταλλάξεις Εδώ:

Ερωτήσεις 1 – 100,     Ερωτήσεις 101 – 200,   Ερωτήσεις 201 – 300

Για ONLINE ΗΛΕΚΤΡΟΝΙΚΑ ΤΕΣΤ ΤΩΝ ΕΡΩΤΗΣΕΩΝ πατήστε ΕΔΩ

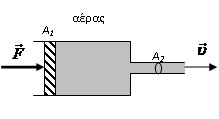
Το καζανάκι της τουαλέτας μιας κατοικίας, τροφοδοτείται από μεγάλη ανοιχτή δεξαμενή  στην ταράτσα, στην οποία η στάθμη του νερού βρίσκεται σε σταθερό ύψος Η = 3,2m από το σωληνάκι τροφοδοσίας (Σ), όπως φαίνεται στο σχήμα 1. Αν g = 10m/s², το νερό θεωρηθεί ιδανικό ρευστό και η ροή στρωτή και μόνιμη:

i) Ποια είναι η ταχύτητα και η αντίστοιχη παροχή του νερού, που μπαίνει στο καζανάκι, από την τρύπα του πλαϊνού τοιχώματος

α) όσο η στάθμη βρίσκεται κάτω από την τρύπα (σχ. 1α);

β) τη στιγμή που η στάθμη βρίσκεται σε ύψος h = 0,4m πάνω από την τρύπα (σχ. 1β);

ii) Το σωληνάκι (Σ) έχει εμβαδό διατομής A = 2cm² και θέλουμε να σταματάει την τροφοδοσία, όταν η στάθμη του νερού φτάσει σε ύψος h πάνω από την τρύπα. Για το σκοπό αυτό υπάρχει ένας μηχανισμός, που αποτελείται από δύο – κολλημένες μεταξύ τους – αβαρείς ράβδους ΚΟ και ΟΛ με OK ┴ OΛ (σχήμα 2). Στο άκρο Κ έχουμε συνδέσει, με άρθρωση, μια πλαστική σφαίρα (πλωτήρας), ενώ στο άκρο Λ επίσης με άρθρωση, έχει συνδεθεί κυλινδρική τάπα εμβαδού . Ο μηχανισμός μπορεί να στρέφεται περί οριζόντιο άξονα, που διέρχεται από το Ο, έτσι ώστε οι ράβδοι και τα κέντρα σφαίρας και τάπας, βρίσκονται διαρκώς στο ίδιο κατακόρυφο επίπεδο. Όταν η στάθμη του νερού φτάσει στο επιθυμητό όριο, η σφαίρα παραμένει βυθισμένη σε ποσοστό 20% του όγκου της στο νερό και η τάπα σφραγίζει την τρύπα διακόπτοντας την παροχή νερού.

Αν (ΟΚ) = 2(OΛ), υπολογίστε το μέτρο

α) της άνωσης που δέχεται η σφαίρα και

β) της δύναμης που δέχεται ο μηχανισμός από την άρθρωση Ο.

iii) Ποια πρέπει να είναι η ακτίνα της σφαίρας;

Απάντηση(Word)

Απάντηση(Pdf)

Στο σχήμα φαίνεται τμήμα κατακόρυφης τομής κυλινδρικής επιφάνειας ακτίνας R = 3,2m, σχήματος τεταρτοκυκλίου. Από το ανώτερο σημείο Α, εκτοξεύεται κατακόρυφα προς τα κάτω μικρό σώμα Σ₁ μάζας m₁ = 2kg, με αρχική ταχύτητα μέτρου υ₀ = 2m/s, το οποίο ολισθαίνει συνεχώς στην κυλινδρική επιφάνεια, κατέρχεται, φτάνει στο κατώτερο σημείο Β του τεταρτοκυκλίου και εισέρχεται σε λείο οριζόντιο επίπεδο με ταχύτητα μέτρου υ₁ = 6m/s. Πάνω σε αυτό το οριζόντιο επίπεδο ηρεμεί το σύστημα των σωμάτων Σ₂ – Σ₃ με το οριζόντιο ελατήριο σταθεράς k = 2000N/m, που τα συνδέει, να βρίσκεται στο φυσικό του μήκος. Το Σ₁ συγκρούεται κεντρικά και ελαστικά με το σύστημα των σωμάτων Σ₂ – Σ₃. Αμέσως μετά την κρούση το σώμα Σ₂ αποκτά αλγεβρική τιμή ταχύτητας υ₂΄=(2/3)υ₁. Δίνεται g = 10m/s².

 α) Αν η κάθετη αντίδραση που ασκείται στο σώμα Σ₁, όταν διέρχεται από το σημείο Β, έχει μέτρο Ν = 42,5Ν, ποιο είναι το μέτρο της ταχύτητας ;

β) Δικαιολογείστε ενεργειακά γιατί το τεταρτοκύκλιο δεν είναι λείο και υπολογίστε το ποσοστό της αρχικής μηχανικής ενέργειας του Σ₁, που έγινε θερμική ενέργεια. Θεωρείστε επίπεδο αναφοράς βαρυτικής δυναμικής ενέργειας, το οριζόντιο επίπεδο, που διέρχεται από το Β.

γ) Υπολογίστε τη μεταβολή της ορμής του σώματος Σ₁ κατά την κίνησή του στο τεταρτοκύκλιο.

δ) Ποια είναι η μάζα m₂ του σώματος Σ₂ και πόση είναι η μεταβολή της κινητικής ενέργειας του Σ₁ εξ αιτίας της κρούσης;

ε) Να μελετήσετε ποιοτικά το είδος της κίνησης που θα εκτελέσουν τα σώματα Σ₂ και Σ₃ μετά την κρούση.

στ) Αν m₃ = 16kg, βρείτε τη μέγιστη συμπίεση του ελατηρίου και τις ταχύτητες των σωμάτων Σ₂ και Σ₃ εκείνη τη στιγμή.

ζ) Υπολογίστε τους ρυθμούς μεταβολής ταχύτητας, ορμής και κινητικής ενέργειας του σώματος Σ₂, τη στιγμή που το ελατήριο έχει τη μέγιστη συμπίεση.

η) Ποιες είναι οι ταχύτητες των σωμάτων Σ₂ και Σ₃ τη στιγμή που το ελατήριο αποκτά για πρώτη φορά μετά την κρούση το φυσικό του μήκος;

Απάντηση (Pdf)