Τα κύματα διαδίδονται με ταχύτητα υ_δ = 10m/s και προέρχονται από δύο σύγχρονες πηγές O₁ και O₂, που ξεκίνησαν να ταλαντώνονται τη χρονική στιγμή t = 0s χωρίς αρχική φάση.

Ένα σημείο Α της επιφάνειας του υγρού απέχει απόσταση r₁ = 2,5m από την Ο₁ με Ο₁Α ┴ Ο₁Ο₂. Η απόσταση των πηγών μεταξύ τους είναι  L = O₁O₂ = 6m.

Ένας ανιχνευτής κυμάτων, ξεκινώντας από το σημείο Α, μπορεί να κινείται στην ημιευθεία Αx για την οποία ισχύει, Αx ∕ ∕ O₁O₂. Δίνεται √42,25 = 6,5.

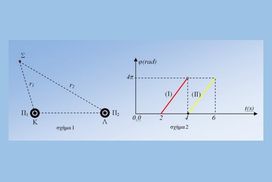
α) Υπολογίστε τη συχνότητα των ταλάντωσης των πηγών.

β) Βρείτε την απόσταση d των σημείων τομής δυο διαδοχικών κροσσών ενίσχυσης, με την ευθεία O₁O₂.

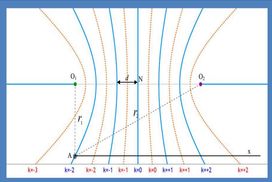
γ) Κάποιος ισχυρίζεται ότι όσοι κροσσοί ενίσχυσης διέρχονται από το ευθύγραμμο τμήμα Ο₁Ο₂ τόσοι διέρχονται και από την ημιευθεία Αx. Συμφωνείτε; Αποδείξτε τον ισχυρισμό σας με παρατήρηση της εικόνας αλλά και θεωρητικά.

δ) Κάποιος ισχυρίζεται ότι όσοι κροσσοί απόσβεσης τέμνουν το ευθύγραμμο τμήμα Ο₁Ν, όπου Ν μέσο της Ο₁Ο₂, τόσοι τέμνουν και το ευθύγραμμο τμήμα Ο₁Α. Συμφωνείτε; Αποδείξτε τον ισχυρισμό σας με παρατήρηση της εικόνας αλλά και θεωρητικά.

ε) Ποια είναι η ελάχιστη αύξηση της συχνότητας των πηγών, που απαιτείται ώστε στο σημείο Α να έχουμε απόσβεση;

Απάντηση 

Απάντηση 

Δυο σύγχρονες πηγές Π₁ και Π₂ αρχίζουν να ταλαντώνονται τη χρονική στιγμή t₀ = 0s, χωρίς αρχική φάση και διεγείρουν σε αρμονική ταλάντωση τα σημεία Κ και Λ της επιφάνειας ηρεμούντος υγρού. Το πλάτος της ταλάντωσης είναι  Α = 0,01m, η περίοδος T = 1s και στην επιφάνεια του υγρού διαδίδονται εγκάρσια κύματα χωρίς αποσβέσεις. Σημείο Σ της επιφάνειας απέχει από τα σημεία Κ και Λ αποστάσεις r₁ = 0,8m και r₂ = 1,2m αντίστοιχα, όπως φαίνεται στο σχήμα 1.
Στο σχήμα 2 βλέπουμε το διάγραμμα της φάσης της ταλάντωσης του σημείου Σ σε συνάρτηση με το χρόνο.
Υποθέστε ότι τα κύματα φτάνουν στο Σ διατηρώντας σταθερό πλάτος.
α) Υπολογίστε την ταχύτητα διάδοσης και το μήκος κύματος.
β) Να εξηγήσετε τη μορφή της γραφικής παράστασης.
γ) Να βρείτε τη χρονική συνάρτηση της φάσης της ταλάντωσης του Σ, μετά τη συμβολή.
δ) Να γράψετε τις εξισώσεις της απομάκρυνσης του Σ σε συνάρτηση με το χρόνο, για 0s ≤ t ≤ 6s και να κάνετε την αντίστοιχη γραφική παράσταση ψ → t σε βαθμολογημένους άξονες.

Απάντηση 

Απάντηση 

Δυο όμοιες σύμφωνες πηγές δημιουργούν κύματα στην επιφάνεια νερού.

Το μήκος κύματος είναι 10 cm και οι πηγές απέχουν 12 cm.

Πόσοι κροσσοί ενισχυτικής συμβολής και πόσοι αποσβετικής συμβολής σχηματίζονται;

Δύο λύσεις:

Σε γραμμικό ελαστικό μέσο, διαδίδεται προς τα δεξιά, με ταχύτητα υ_δ = 10cm/s τετραγωνικός παλμός πλευράς α = 4cm, όπως στο σχήμα.

Η αρχή (μέτωπο) του παλμού, απέχει από τον τοίχο L = 20cm.

i) Βρείτε το σχήμα της χορδής τις χρονικές στιγμές

α) t₁ = 2,1s

β) t₂ = 2,3s

ii) Υπολογίστε επίσης τη μετατόπιση ενός υλικού σημείου Σ του μέσου, που βρίσκεται 3cm αριστερά του τοίχου, τις παραπάνω χρονικές στιγμές.

Απάντηση 

Απάντηση 

Ένα διάμηκες ηχητικό κύμα συχνότητας f = 425Hz, δημιουργείται από το διαπασών S και εισέρχεται στο σωλήνα του σχήματος (σωλήνας Quincke). Το τμήμα Γ είναι σταθερού μήκους ενώ το τμήμα Β είναι κινητό και μπορούμε να αυξομειώνουμε το μήκος του. Αρχικά το τμήμα Β είναι τέρμα αριστερά δηλαδή απόσταση x = 0. Ο ήχος διασπάται σε δύο ηχητικά κύματα πλάτους ίδιου πλάτους Α, που ακολουθούν τις διαδρομές SBR και SΓR, για τις οποίες γνωρίζουμε την αρχική διαφορά SBR – SΓR = s₂ – s₁ = 0,8m. Στη συνέχεια τα δυο κύματα συμβάλλουν στο σημείο του σωλήνα, λίγο πριν την έξοδο στο δέκτη R. Η ταχύτητα του ήχου στον αέρα είναι υ_ηχ = 340m/s και θεωρούμε αμελητέα τη μεταβολή του πλάτους των δύο κυμάτων, μέχρι τη στιγμή της συμβολής.
i) Ο δέκτης λαμβάνει μέγιστο ή ελάχιστο πλάτος ως αποτέλεσμα της συμβολής;
ii) Διερευνείστε το πλάτος του ήχου που θα λάβει ο δέκτης R, αν από την αρχική του θέση ο κινητός σωλήνας εξέλθει επιπλέον κατά
α) x = 0,1m
β) x = 0,2m
γ) x = 0,4m
iii) Μπορείτε να βρείτε μια χρησιμότητα αυτού του σωλήνα;
iv) Τα δυο ηχητικά κύματα που φτάνουν στο δέκτη, μπορούν πραγματικά να έχουν το ίδιο πλάτος;
v) Για καθηγητές
Αν η ένταση του ήχου όταν ανιχνεύουμε μέγιστο είναι I₁ = 0,09W/m² και όταν ανιχνεύουμε ελάχιστο I₂ = 0,01W/m² ποιος είναι ο λόγος των πλατών, που φτάνουν στον ανιχνευτή;

Απάντηση 

Απάντηση