Συνέχεια 

Συνέχεια 

Στα παρακάτω σχήματα βλέπουμε δυο γραφικές παραστάσεις (I) και (ΙΙ) της έντασης ανά μονάδα μήκους της σκεδαζόμενης μονοχρωματικής ακτινοβολίας ακτίνων Χ, σε συνάρτηση με το μήκος κύματος, σε ένα πείραμα που μελετάμε το φαινόμενο Compton. Η προσπίπτουσα ακτινοβολία έχει μήκος κύματος λ και οι κατανομές της έντασης έχουν ληφθεί για δύο διαφορετικές γωνίες σκέδασης.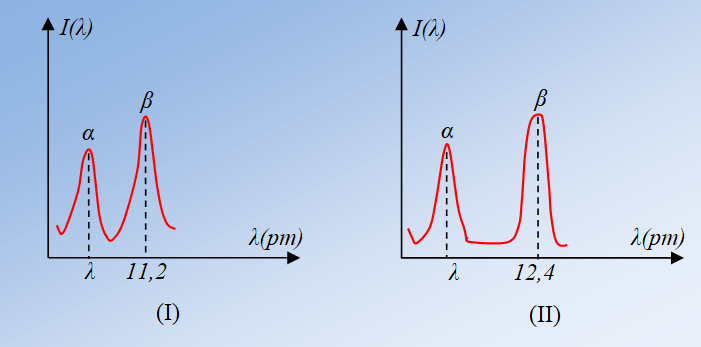

i) Ποια από τις παρακάτω προτάσεις είναι σωστή και γιατί; Μπορείτε να εξηγήσετε γιατί εμφανίζονται δυο κορυφές;

α) Η κορυφή α αντιστοιχεί σε σκεδαζόμενη ακτινοβολία από χαλαρά συνδεδεμένα ηλεκτρόνια ενώ η κορυφή β σε σκεδαζόμενη ακτινοβολία από ισχυρά συνδεδεμένα ηλεκτρόνια του στόχου.

β) Η κορυφή β αντιστοιχεί σε σκεδαζόμενη ακτινοβολία από χαλαρά συνδεδεμένα ηλεκτρόνια ενώ η κορυφή α σε σκεδαζόμενη ακτινοβολία από ισχυρά συνδεδεμένα ηλεκτρόνια του στόχου.

γ) Και οι δύο κορυφές αντιστοιχούν σε σκέδαση από ελεύθερα ηλεκτρόνια του στόχου.

ii) Αν ξέρουμε ότι οι γραφικές παραστάσεις αντιστοιχούν σε γωνίες σκέδασης 60⁰ ή 90⁰, να αντιστοιχίσετε τις γωνίες με τις γραφικές παραστάσεις, εξηγώντας την επιλογή σας.

iii) Η ποσότητα  λ_C = h/mc που βρίσκεται στην εξίσωση του Compton, λέγεται μήκος κύματος Compton. Υπολογίστε το μήκος κύματος Compton και το μήκος κύματος λ της προσπίπτουσας ακτινοβολίας.

iv) Στην περίπτωση της σκέδασης του φωτονίου κατά 60⁰:

α) βρείτε την ορμή του εκδιωχθέντος ηλεκτρονίου. Δίνεται η σταθερά του Planck h = 6,6∙10^-34Js.

β) βρείτε την κινητική ενέργεια του εκδιωχθέντος ηλεκτρονίου. Για την ενέργεια των φωτονίων χρησιμοποιείστε τον τύπο: Ε_ph =(1240eV∙nm / λ) → eV  

v) Ποιο ποσοστό της ενέργειας του φωτονίου πήρε το ηλεκτρόνιο;

Απάντηση 

Απάντηση 

Α. Πηγές φωτός

Οι πιο κοινές πηγές φωτός είναι

α) Θερμαινόμενα στερεά, π.χ. νήμα από W(βολφράμιο) λυχνίας πυρακτώσεως.

β) Αέρια με τη βοήθεια ηλεκτρικής εκκένωσης, π.χ. λυχνία με Ne(Νέον).

γ) Φωτοδίοδοι (Light Emitting Diodes – LED), που αποτελούνται από ημιαγωγούς Ga, As, In κ.λ.π.

Το εκπεμπόμενο φως το αναλύουμε με ένα φασματόμετρο μετρώντας την φασματική αφετική ικανότητα Ι_λ, δηλαδή την ένταση της ακτινοβολίας ανά μονάδα μήκους κύματος.

Συνέχεια 

Συνέχεια 

Α. Από τη Θερμοδυναμική της Β΄τάξης ξέρουμε (;) ότι η μέση κινητική ενέργεια των μορίων ιδανικού αερίου είναι K_μ = (3/2) k_ΒΤ όπου k_B = 8,6∙10⁻⁵ eV/K η σταθερά του Boltzmann και Τ η απόλυτη θερμοκρασία του αερίου.

Σύμφωνα με την Κλασική Στατιστική Φυσική, τα άτομα των υλικών όταν ταλαντώνονται έχουν αντίστοιχα θερμική ενέργεια Ε_Θ = k_ΒΤ 

Υπολογίστε την ενέργεια αυτή σε eV για θερμοκρασία περιβάλλοντος Τ = 300Κ.

Β. Για έναν τυπικό μοριακό δεσμό, η σταθερά επαναφοράς του ταλαντωτή είναι της τάξης των δεκάδων ως εκατοντάδων N/m. Έστω δύο άτομα με:

• μικρό k₁ = 10N/m (μαλακό «ελατήριο)
• μεγάλο k₂ =1000N/m (σκληρό «ελατήριο»)

• Ας θεωρήσουμε πλάτος ταλάντωσης, 1Ångström (1A˚= 10⁻¹⁰ m).

Υπολογίστε σε eVτην ενέργεια ταλάντωσης κάθε ατόμου. Αν θεωρήσουμε μάζα για τα άτομα m = 10^-26kg, ποιες είναι οι αντίστοιχες συχνότητες ταλάντωσης; Δίνεται √10 = π.

Γ. Αν η σταθερά του Planck είναι h = 4,13∙10⁻¹⁵eV∙s, βρείτε το κβάντο ενέργειας κάθε ταλαντωτή.

Δ. Μπορείτε να εξηγήσετε τώρα σύμφωνα με την Κβαντική Φυσική, γιατί οι υψηλής συχνότητας ταλαντωτές σε θερμοκρασία περιβάλλοντος δεν ενεργοποιούνται;

Απάντηση 

Απάντηση 

Εργασία με την προσομοίωση «Φάσμα μελανού σώματος»

Ο σύνδεσμος της προσομοίωσης: ‪Φάσμα μελανού σώματος

Θα χρησιμοποιήσουμε την προσομοίωση, για να διερευνήσουμε πώς το φάσμα της ηλεκτρομαγνητικής ακτινοβολίας, που εκπέμπεται από ένα μέλαν σώμα, επηρεάζεται από τη θερμοκρασία του. Μπορούμε να παρατηρούμε την περιοχή του φάσματος της ηλεκτρομαγνητικής ακτινοβολίας  που εκπέμπει, το μήκος κύματος αιχμής και την αντίστοιχη ένταση ανά μονάδα μήκους κύματος (φασματική αφετική ικανότητα). Ταυτόχρονα βλέπουμε και συνολική ένταση (εμβαδόν καμπύλης), που εκπέμπεται σε όλα τα μήκη κύματος.

Ερωτήσεις 

α) Η θερμοκρασία των αστεριών στο σύμπαν ποικίλλει ανάλογα με τον τύπο του αστεριού και την ηλικία του. Εξετάζοντας τη μορφή του φάσματος του φωτός που εκπέμπεται από ένα αστέρι, μπορούμε να πούμε κάτι για τη μέση θερμοκρασία της επιφάνειάς του.
i) Αν παρατηρήσουμε το φάσμα ενός αστεριού και βρούμε ότι η μέγιστη ισχύς εμφανίζεται στο σύνορο μεταξύ κόκκινου και υπέρυθρου φωτός, ποια είναι κατά προσέγγιση η επιφανειακή θερμοκρασία του αστεριού;
ii) Αν παρατηρήσουμε το φάσμα ενός αστεριού και βρούμε ότι η μέγιστη ισχύς εμφανίζεται στο σύνορο μεταξύ μπλε και υπεριώδους φωτός, ποια είναι η επιφανειακή θερμοκρασία του αστεριού;
β) Οι λαμπτήρες λειτουργούν στους 2500K.
i) Ποιο είναι το μήκος κύματος στο οποίο εκπέμπεται η μεγαλύτερη ισχύς για έναν λαμπτήρα;
ii) Εξηγήστε γιατί οι λαμπτήρες πυρακτώσεως σπαταλούν πολλή ενέργεια.
γ) i) Διερευνήστε πώς το παρατηρούμενο φάσμα επηρεάζεται από τη μεταβολή της θερμοκρασίας.
iii) Σημειώστε τις σωστές ή λανθασμένες προτάσεις:
1. Αν μειώσετε τη θερμοκρασία ενός σώματος, η συνολική ποσότητα ισχύος που εκπέμπεται θα αυξηθεί σε ορισμένες περιπτώσεις.
2. Αν μειώσετε τη θερμοκρασία ενός σώματος, η συνολική ποσότητα ισχύος που εκπέμπεται μειώνεται σε όλες τις περιπτώσεις.
3. Αν αυξήσετε την επιφάνεια ενός σώματος, αλλά αφήσετε τη θερμοκρασία του αμετάβλητη, τότε το μεγαλύτερο μέρος της συνολικής του ισχύος θα εκπέμπεται ως ακτινοβολία υπερύθρων.
δ) Διερευνήσετε τις αλλαγές στην ποσότητα του εκπεμπόμενου φωτός στα ορατά μήκη κύματος, αλλάζοντας  τη θερμοκρασία από 2500K σε 2000K.
Ποια είναι κατά προσέγγιση η αναλογία μεταξύ της ισχύος που εκπέμπεται στα 500nm στους 2000K και της ισχύος στα 500nm στους 2500K;
ε) Ανεβάζετε τον επιλογέα ώστε η θερμοκρασία του νήματος να φτάσει τους 2600K. Το νήμα του λαμπτήρα έχει επιφάνεια S = 6,45∙10^-4 m² και ο συντελεστής θερμικής εκπομπής e = 0,8. Πόση ηλεκτρική ενέργεια πρέπει να καταναλώνει;
στ) Ο νόμος Wien δίνει τη σχέση μεταξύ της θερμοκρασίας Τ ενός μέλανος σώματος και του μήκους κύματος αιχμής λ_max.
i) Συμπληρώστε τον παρακάτω πίνακα:

Θερμοκρασία Τ (K)	Μήκος κύματος λmax (nm)	λmax ∙T(x 10-3 K∙m)
2000
3000
4000
5000
6000
10000
		Μέση τιμή:

ii) Επαληθεύεται ο νόμος Wien; Να κάνετε την αντίστοιχη γραφική παράσταση σε βαθμολογημένους άξονες.
ζ) Γιατί δε βλέπουμε τη θερμική ακτινοβολία των σωμάτων μέσα στο δωμάτιό μας;
η) Πόση ισχύ εκπέμπει ένας άνθρωπος;
θ) Στη διπλανή εικόνα φαίνεται μια ηλεκτρική εστία διαμέτρου 12cm, ισχύος 2500W.
Σε ποια θερμοκρασία θα φτάσει όταν το ανάψουμε; Τι χρώμα θα φαίνεται τότε;

Απάντηση 

Απάντηση 

Πηγή LED -Χρώμα	λ(nm)
Ερυθρό	620
Πορτοκαλί	586
Πράσινο	530
Μπλε	485

Εκτελούμε το πείραμα παρατήρησης φωτοηλεκτρικού φαινομένου στο εργαστήριο, χρησιμοποιώντας ως φωτεινή πηγή μονοχρωματικού φωτός λάμπες LED, οι οποίες εκπέμπουν μήκη κύματος, που φαίνονται στον παραπάνω πίνακα.

Η φωτοκάθοδος της συσκευής είναι από Cs (καίσιο), που έχει έργο εξαγωγής

φ = 2,87 ∙ 10^-19J.

α)  Θεωρώντας γνωστή τη σχέση Ε_ph = 1242(eV∙nm) / λ(nm), εξετάστε ποιες από τις λάμπες μπορούν να χρησιμοποιηθούν για την εξαγωγή φωτοηλεκτρονίων.

β) Χρησιμοποιώντας τις λάμπες που βρήκατε στο ερώτημα (α) συμπληρώστε τον παρακάτω πίνακα:

Πηγή Led -Χρώμα	λ(nm)	f(*1014Hz)	Εph (eV)	Kmax (eV)	V0 (V)

Δίνεται η ταχύτητα φωτός στο κενό ή αέρα c = 3∙10⁸m/s.

γ) Να κάνετε τη γραφική παράσταση K_max → f σε βαθμολογημένους άξονες, θεωρώντας ότι είναι ευθεία. Με τη βοήθεια της γραφικής παράστασης υπολογίστε τη σταθερά του Planck και το σχετικό σφάλμα μέτρησης, αν η τιμή της σταθεράς είναι h = 6,63∙10^-34Js.

δ) Χρησιμοποιώντας τη μπλε λάμπα, πλησιάζουμε τη φωτεινή πηγή στη μισή απόσταση (από d σε d/2), σε σχέση με αυτή που βρισκόταν ως τώρα.

δ1) Τι θα συμβεί με τη φωτονική ροή πάνω στην κάθοδο;

δ2) Να κάνετε ποιοτική γραφική παράσταση της έντασης του φωτορεύματος i σε συνάρτηση με την τάση V_AK (ανόδου – καθόδου), πριν και μετά το πλησίασμα της φωτεινής πηγής. Υποθέτουμε ότι κάθε φωτόνιο εξάγει ένα ηλεκτρόνιο.

ε) Να κάνετε ποιοτική γραφική παράσταση της έντασης του φωτορεύματος i σε συνάρτηση με την τάση V_AK (ανόδου – καθόδου), για την κόκκινη και τη μπλε λάμπα τοποθετημένες στην ίδια απόσταση από τη φωτοκάθοδο. Υποθέτουμε ότι κάθε φωτόνιο εξάγει ένα ηλεκτρόνιο.

Απάντηση 

Απάντηση 

A) H ένταση ανά μονάδα μήκους κύματος, του ηλιακού φωτός που φτάνει στη Γη, δίνεται από το διάγραμμα 1:

α) Πόσο είναι το εμβαδό κάτω από τη γκρι γραφική παράσταση; Δικαιολογείστε την απάντησή σας.
β) Η απόσταση της Γης από την επιφάνεια του Ήλιου είναι d = 1,5∙10¹¹m. Ποιος είναι ο ρυθμός εκπομπής φωτεινής ενέργειας από τον Ήλιο; Θεωρούμε τον Ήλιο ως σημειακή φωτεινή πηγή, που εκπέμπει ομοιόμορφα προς όλες τις διευθύνσεις.
γ) Υπολογίστε το ρυθμό με τον οποίο φωτόνια με το μήκος κύματος αιχμής, χτυπούν το γυαλί του φακού ενός τηλεσκοπίου με διάμετρο φακού δ = 200mm, αν υποθέσουμε ότι το φως του Ήλιου είναι μονοχρωματικό με αυτό το μήκος κύματος.

B) Στην επόμενη εικόνα βλέπουμε κάποια πολύ γνωστά άστρα και το χρώμα τους στην περιοχή του ορατού φωτός. Οι θερμοκρασίες τους – με τυχαία σειρά – μπορεί να είναι:

Συνέχεια 

 

Σε ένα ιδανικό μέλαν σώμα, δύο άτομα α και β ταλαντώνονται με την ίδια ενέργεια Ε_i. Το άτομο α απορροφά ένα φωτόνιο με συχνότητα f₁ = f, ενώ το άτομο β απορροφά ένα φωτόνιο με συχνότητα f₂ = 3f.

i) Να σχεδιάσετε ένα ποιοτικό διάγραμμα ενέργειας – συχνότητας (Ε-f) για τα ενεργειακά άλματα που κάνουν τα άτομα.

ii) Τα άτομα α και β αποδιεγείρονται. Ποιες από τις παρακάτω προτάσεις πιστεύετε ότι είναι σωστές ή λάθος; Δικαιολογείστε τις απαντήσεις σας.

α) Το άτομο α θα εκπέμψει μόνο ένα φωτόνιο συχνότητας  f₁, επιστρέφοντας στην Ε_i.

β) Το άτομο β είναι πιο πιθανό να εκπέμψει ένα φωτόνιο συχνότητας  f₂, επιστρέφοντας στην Ε_i.

γ) Το άτομο β είναι πιο πιθανό να εκπέμψει τρία φωτόνια συχνότητας  f₁, επιστρέφοντας στην Ε_i.

iii) Σχεδιάστε ένα ποιοτικό διάγραμμα ενεργειακών σταθμών, που να φαίνονται οι εκπομπές φωτονίων από τα άτομα α και β, κατά την αποδιέγερσή τους.

iv) Μπορείτε τώρα να εξηγήσετε γιατί η γραφική παράσταση της φασματικής αφετικής ικανότητας (έντασης ανά μονάδα μήκους κύματος) του μέλανος σώματος, τείνει στο μηδέν για πολύ μικρά ή πολύ μεγάλα μήκη κύματος;

Απάντηση 

 

Σε ένα πείραμα μελέτης του φαινομένου Compton, θέλουμε ένα ακίνητο ηλεκτρόνιο, μετά τη σκέδαση του προσπίπτοντος φωτονίου, να αποκτήσει κινητική ενέργεια Κ = 32keV.

α) Ποια είναι η ελάχιστη ενέργεια Ε ενός φωτονίου, που μπορεί να προκαλέσει αυτή τη σκέδαση;

β) Για καθηγητές

Η ταχύτητα του ηλεκτρονίου μπορεί να υπολογιστεί με τη βοήθεια της Κλασσικής Φυσικής;

Δίνονται μάζα ηρεμίας ηλεκτρονίου m = 9,1∙10^-31kg, ταχύτητα φωτός στο κενό c = 3 ∙ 10⁸m/s και 1eV = 1,6 ∙ 10^-19J

Απάντηση