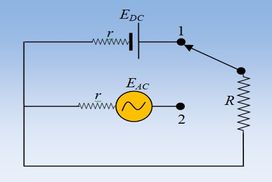
Η αντίσταση R = 3Ω, του διπλανού σχήματος βρίσκεται στο όριο υπερθέρμανσης και καταστροφής, όταν καταναλώνει ισχύ P = 27W. Με τον διακόπτη στη θέση 1, συνδέουμε την πηγή συνεχούς, που έχει εσωτερική αντίσταση r = 1Ω.
α) Ποια πρέπει να είναι η ΗΕΔ ΕDC αυτής της πηγής;
Θέλουμε να μεταφέρουμε τον διακόπτη στη θέση 2, συνδέοντας πηγή εναλλασσόμενης τάσης, που προέρχεται από στρεφόμενο ορθογώνιο πλαίσιο, με διαστάσεις α = 30cm, β = 40cm, μέσα σε μαγνητικό πεδίο έντασης Β = 0,01Τ κάθετα στον άξονα περιστροφής του. Το πλαίσιο έχει Ν = 1000 σπείρες και στρέφεται με γωνιακή ταχύτητα ω = 10√2rad/s.
β) Κάποιος ισχυρίζεται ότι δεν πρέπει να το κάνουμε γιατί ο αντιστάτης θα λειώσει. Έχει δίκιο;
γ) Να γράψετε την εξίσωση i = f(t) του εναλλασσόμενου ρεύματος, που θα παρέχει αυτή η πηγή σε συνάρτηση με το χρόνο, αν την t0 = 0s, i = 0A και το εμβαδικό διάνυσμα του πλαισίου είναι ομόρροπο με το διάνυσμα . Στη συνέχεια να την παραστήσετε γραφικά για μια περίοδο στο ίδιο σύστημα αξόνων με το αντίστοιχο ρεύμα IDC, που παρέχει η πηγή συνεχούς.
δ) Ποιες χρονικές στιγμές στη διάρκεια της πρώτης ημιπεριόδου έχουμε i = IAC; Σε τι ποσοστό του χρόνου μιας περιόδου αντιστοιχεί ο συνολικός χρόνος υπέρβασης του ορίου ρεύματος;
ε) Τι αλλαγές θα προτείνατε για την πηγή στρεφόμενου πλαισίου, ώστε να παρέχει την επιτρεπόμενη τάση στην αντίσταση;
στ) Αν υπολογίζαμε τη μέση ισχύ θα μπορούσαμε να εξετάσουμε αν κινδυνεύει να καταστραφεί ο αντιστάτης;






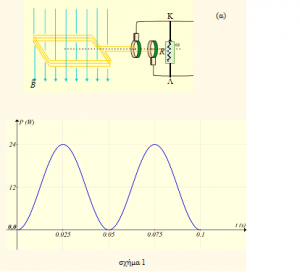




 Στο δοχείο του σχήματος, με ανένδοτα τοιχώματα, ιδανικούς μονωτές της θερμότητας, βρίσκονται n = (245/3R) mol ιδανικού μονατομικού αερίου, όπου R η παγκόσμια σταθερά των ιδανικών αερίων. Με τη βοήθεια του αντιστάτη, που παρουσιάζει αντίσταση R1 = 5Ω, η θερμοκρασία του αερίου αυξάνεται με σταθερό ρυθμό λ = dT/dt = 0,1K/s. Στον αντιστάτη διαβιβάζονται ταυτόχρονα δύο εναλλασσόμενα ρεύματα με εξισώσεις Ι1 = 3ημ(ωt) (S.I.) και Ι2 = 5ημ(ωt + φ0) (S.I.)
Στο δοχείο του σχήματος, με ανένδοτα τοιχώματα, ιδανικούς μονωτές της θερμότητας, βρίσκονται n = (245/3R) mol ιδανικού μονατομικού αερίου, όπου R η παγκόσμια σταθερά των ιδανικών αερίων. Με τη βοήθεια του αντιστάτη, που παρουσιάζει αντίσταση R1 = 5Ω, η θερμοκρασία του αερίου αυξάνεται με σταθερό ρυθμό λ = dT/dt = 0,1K/s. Στον αντιστάτη διαβιβάζονται ταυτόχρονα δύο εναλλασσόμενα ρεύματα με εξισώσεις Ι1 = 3ημ(ωt) (S.I.) και Ι2 = 5ημ(ωt + φ0) (S.I.)