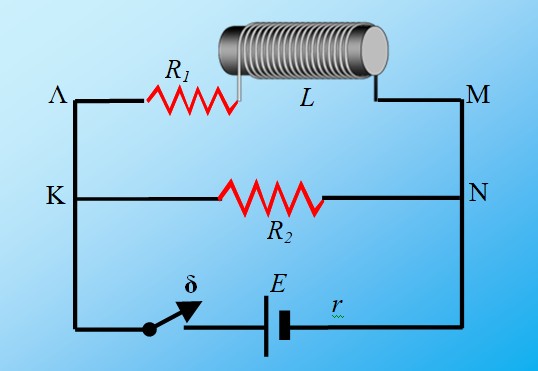
 Στο κύκλωμα του σχήματος δίνονται R1 = 3Ω, R2 = 6Ω, η πηγή ιδανική με ΗΕΔ Ε = 12V και το πηνίο ιδανικό με συντελεστή αυτεπαγωγής L = 0,3H.
Στο κύκλωμα του σχήματος δίνονται R1 = 3Ω, R2 = 6Ω, η πηγή ιδανική με ΗΕΔ Ε = 12V και το πηνίο ιδανικό με συντελεστή αυτεπαγωγής L = 0,3H.
i) Τη χρονική στιγμή t0 = 0s κλείνουμε το διακόπτη δ και τον ανοίγουμε ακαριαία τη χρονική στιγμή t1 = 1s. Δεδομένου ότι το χρονικό αυτό διάστημα είναι αρκετό για την αποκατάσταση του ρεύματος, βρείτε την ένταση του ρεύματος σε κάθε κλάδο του κυκλώματος και την αλγεβρική τιμή της ΗΕΔ αυτεπαγωγής στο πηνίο
α) τη χρονική στιγμή t = 0+s (ποσοτικά)
β) μια χρονική στιγμή 0s < t < 1s (ποιοτικά)
γ) τη χρονική στιγμή t = 1s (ποσοτικά)
ii) Μετά το άνοιγμα του διακόπτη και με δεδομένο ότι τη χρονική στιγμή t2 = 2s έχει τελειώσει το φαινόμενο της αυτεπαγωγής, βρείτε την ένταση του ρεύματος σε κάθε κλάδο του κυκλώματος και την αλγεβρική τιμή της ΗΕΔ αυτεπαγωγής στο πηνίο
α) τη χρονική στιγμή t = 1+s (ποσοτικά)
β) Μια χρονική στιγμή 1s < t < 2s (ποιοτικά)
γ) τη χρονική στιγμή t = 2s (ποσοτικά)
iii) Να κάνετε τη γραφική παράσταση της έντασης του ρεύματος σε συνάρτηση με το χρόνο, που διαρρέει κάθε κλάδο του κυκλώματος πριν και μετά το άνοιγμα του διακόπτη.
iv) Να κάνετε τη γραφική παράσταση της ΗΕΔ αυτεπαγωγής στο πηνίο σε συνάρτηση με το χρόνο, πριν και μετά το άνοιγμα του διακόπτη.
v) Κάποια στιγμή t1 όπου 0s < t1 < 1s η ένταση του ρεύματος που δίνει η πηγή είναι i = 3A. Βρείτε τις ενεργειακές μετατροπές, υπολογίζοντας την ισχύ που ανταλλάσσει με το κύκλωμα κάθε δίπολο του κυκλώματος.
vi) Κάποια στιγμή t1 όπου 1s < t2 < 2s η ένταση του ρεύματος που διαρρέει το κύκλωμα είναι i1 = 3A. Βρείτε τις ενεργειακές μετατροπές, υπολογίζοντας την ισχύ που ανταλλάσσει με το κύκλωμα κάθε δίπολο του κυκλώματος.






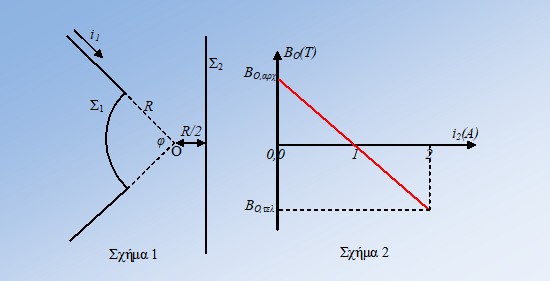
 Διαθέτουμε δυο λεπτά σύρματα Σ1 και Σ2 πολύ μεγάλου μήκους. Τα κάμπτουμε ώστε να δημιουργήσουμε δυο αγωγούς, τους οποίους συνδέουμε σε σειρά όπως στο σχήμα 1. Ο αγωγός Σ που σχηματίζεται έχει ένα ημικύκλιο ακτίνας R και δυο ημιευθείες Αx, Γy. Όταν διαρρέει τον αγωγό Σ ρεύμα έντασης I, η ένταση του μαγνητικού πεδίου στο κέντρο Ο του ημικυκλίου είναι B. Αποσυνδέουμε το σύστημα, κάμπτουμε εκ νέου τα σύρματα σε σχήμα ορθής γωνίας, τα τοποθετούμε όπως στο σχήμα 2 και τα τροφοδοτούμε με ρεύμα ίδιας έντασης Ι΄. Στο ευθύγραμμο τμήμα ΔΚ, που συνδέει τις κορυφές των ορθών γωνιών το σημείο Ο είναι μέσον με ΔΟ = ΟΚ = R. Αφού βρείτε τη φορά του ρεύματος σε κάθε αγωγό, υπολογίστε ποια από τις παρακάτω είναι η τιμή της έντασης Ι΄, ώστε στο σημείο Ο το μαγνητικό πεδίο να έχει πάλι ένταση B.
Διαθέτουμε δυο λεπτά σύρματα Σ1 και Σ2 πολύ μεγάλου μήκους. Τα κάμπτουμε ώστε να δημιουργήσουμε δυο αγωγούς, τους οποίους συνδέουμε σε σειρά όπως στο σχήμα 1. Ο αγωγός Σ που σχηματίζεται έχει ένα ημικύκλιο ακτίνας R και δυο ημιευθείες Αx, Γy. Όταν διαρρέει τον αγωγό Σ ρεύμα έντασης I, η ένταση του μαγνητικού πεδίου στο κέντρο Ο του ημικυκλίου είναι B. Αποσυνδέουμε το σύστημα, κάμπτουμε εκ νέου τα σύρματα σε σχήμα ορθής γωνίας, τα τοποθετούμε όπως στο σχήμα 2 και τα τροφοδοτούμε με ρεύμα ίδιας έντασης Ι΄. Στο ευθύγραμμο τμήμα ΔΚ, που συνδέει τις κορυφές των ορθών γωνιών το σημείο Ο είναι μέσον με ΔΟ = ΟΚ = R. Αφού βρείτε τη φορά του ρεύματος σε κάθε αγωγό, υπολογίστε ποια από τις παρακάτω είναι η τιμή της έντασης Ι΄, ώστε στο σημείο Ο το μαγνητικό πεδίο να έχει πάλι ένταση B.