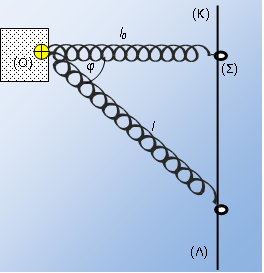
Ένα σωματίδιο με μάζα m, φορτίο q και αρχική ταχύτητα μέτρου υ0 = 8×103 m/s εκτοξεύεται σε ένα ομογενές ηλεκτρικό πεδίο ανάμεσα σε δύο παράλληλες μεταλλικές πλάκες μήκους L = 48cm, όπως στο σχήμα. Το ηλεκτρικό πεδίο μεταξύ των πλακών κατευθύνεται προς τα κάτω και η ένταση έχει μέτρο E = 500 N/C. Ας υποθέσουμε ότι το πεδίο είναι μηδέν έξω από την περιοχή μεταξύ των πλακών. Η απόσταση μεταξύ των πλακών είναι αρκετά μεγάλη ώστε το σωματίδιο να περάσει ανάμεσα στις πλάκες χωρίς να χτυπήσει την κάτω πλάκα και να εξέλθει από το πεδίο στο σημείο Α. Μια φθορίζουσα οθόνη απέχει s = 36cm από την άκρη των παράλληλων πλακών. Το σωματίδιο προσπίπτει στην οθόνη σε ένα σημείο Γ, έχοντας υποστεί συνολική κατακόρυφη απόκλιση ΒΓ = d = 9cm από την αρχική διεύθυνση της ταχύτητας εισόδου στο πεδίο. Αγνοήστε τη βαρύτητα και την αντίσταση του αέρα.
Ένα σωματίδιο με μάζα m, φορτίο q και αρχική ταχύτητα μέτρου υ0 = 8×103 m/s εκτοξεύεται σε ένα ομογενές ηλεκτρικό πεδίο ανάμεσα σε δύο παράλληλες μεταλλικές πλάκες μήκους L = 48cm, όπως στο σχήμα. Το ηλεκτρικό πεδίο μεταξύ των πλακών κατευθύνεται προς τα κάτω και η ένταση έχει μέτρο E = 500 N/C. Ας υποθέσουμε ότι το πεδίο είναι μηδέν έξω από την περιοχή μεταξύ των πλακών. Η απόσταση μεταξύ των πλακών είναι αρκετά μεγάλη ώστε το σωματίδιο να περάσει ανάμεσα στις πλάκες χωρίς να χτυπήσει την κάτω πλάκα και να εξέλθει από το πεδίο στο σημείο Α. Μια φθορίζουσα οθόνη απέχει s = 36cm από την άκρη των παράλληλων πλακών. Το σωματίδιο προσπίπτει στην οθόνη σε ένα σημείο Γ, έχοντας υποστεί συνολική κατακόρυφη απόκλιση ΒΓ = d = 9cm από την αρχική διεύθυνση της ταχύτητας εισόδου στο πεδίο. Αγνοήστε τη βαρύτητα και την αντίσταση του αέρα.
α) Ποιο είναι το είδος του φορτίου του σωματιδίου;
β) Αν λ = q/m το ειδικό φορτίου του σωματιδίου αποδείξτε ότι η κατακόρυφη απόκλιση h κατά την έξοδο από το πεδίο, δίνεται από τη σχέση: h = ½ λΕtεξ2
όπου tεξ η χρονική στιγμή εξόδου του σωματιδίου από το πεδίο.
γ) Υπολογίστε το ειδικό φορτίο λ = q/m του σωματιδίου.
δ) Στο σύστημα ορθογωνίων αξόνων ΧΟY, του σχήματος προσδιορίστε τις συντεταγμένες του σημείου Α.
ε) Ποια είναι η ταχύτητα του σωματιδίου τη στιγμή της εξόδου του από το ηλεκτρικό πεδίο;



 Ένα ηλεκτρόνιο εκτοξεύεται με αρχική ταχύτητα μέτρου υ0 = 1,6 ∙ 106m/s μέσα στο ομογενές ηλεκτρικό πεδίο, ανάμεσα σε δύο παράλληλες πλάκες Α και Β, όπως στο σχήμα. Το ηλεκτρόνιο έχει φορτίο qe = -1,6 ∙ 10-19C, μάζα me = 9 ∙ 10-31kg και εισέρχεται στο πεδίο στο σημείο Ο που βρίσκεται στο μέσον της απόστασης μεταξύ των δύο πλακών. Η ταχύτητα εκτόξευσης έχει διεύθυνση παράλληλη προς τις πλάκες, οι οποίες έχουν μήκος L = 2cm και απέχουν μεταξύ τους απόσταση d = 1cm. Αγνοούμε το βαρυτικό πεδίο της Γης.
Ένα ηλεκτρόνιο εκτοξεύεται με αρχική ταχύτητα μέτρου υ0 = 1,6 ∙ 106m/s μέσα στο ομογενές ηλεκτρικό πεδίο, ανάμεσα σε δύο παράλληλες πλάκες Α και Β, όπως στο σχήμα. Το ηλεκτρόνιο έχει φορτίο qe = -1,6 ∙ 10-19C, μάζα me = 9 ∙ 10-31kg και εισέρχεται στο πεδίο στο σημείο Ο που βρίσκεται στο μέσον της απόστασης μεταξύ των δύο πλακών. Η ταχύτητα εκτόξευσης έχει διεύθυνση παράλληλη προς τις πλάκες, οι οποίες έχουν μήκος L = 2cm και απέχουν μεταξύ τους απόσταση d = 1cm. Αγνοούμε το βαρυτικό πεδίο της Γης.