Η ράβδος περιστρέφεται, αναγκάζοντας τη μπάλα να κινείται με σταθερή ταχύτητα μέτρου υ, σε έναν οριζόντιο κύκλο ακτίνας R. Τα νήματα έχουν το καθένα μήκος L συνδέονται τη ράβδο με δακτυλίους που περιστρέφονται ελεύθερα χωρίς τριβές γύρω από τη ράβδο. Κάθε νήμα είναι τεντωμένο και σχηματίζει γωνία θ με την κατακόρυφο.

α) Σχεδιάστε στη σφαίρα τις δυνάμεις και το διάνυσμα της κεντρομόλου επιτάχυνσης.

β) Πάρτε πάνω στη σφαίρα ένα σύστημα ορθογωνίων αξόνων Χ΄X οριζόντιο και Ψ΄Ψ κατακόρυφο και γράψτε τις δύο εξισώσεις στο S.I., που προκύπτουν από την εφαρμογή του δεύτερου νόμου του Νεύτωνα στη σφαίρα, για κάθε άξονα. Δίνονται: m = 3kg, L = 1,60m, θ = 60° , g = 10m/s² και υ = 8 m/s.

γ) Βρείτε το μέτρο κάθε τάσης νήματος. Ήταν αναμενόμενο το αποτέλεσμα;

Απάντηση 

Απάντηση 

Υλικό σημείο Ρ κινείται ευθύγραμμα και ομαλά με σταθερή ταχύτητα υ. Την κίνηση παρακολουθεί παρατηρητής, που βρίσκεται στην αρχή Ο του συστήματος ΧΟΨ ορθογωνίων αξόνων, που φαίνεται στο παρακάτω σχήμα.

Η τροχιά του Ρ τέμνει τον άξονα ΟΨ στο σημείο (0, α) και η απόσταση του Ρ από το Ο καθορίζεται από το διάνυσμα θέσης r.

α) Γιατί το υλικό σημείο Ρ έχει γωνιακή ταχύτητα ;

β) Να αποδείξετε ότι το μέτρο της, είναι ω = υ α / r²

Συνέχεια 

Συνέχεια 

Σε μια ταινία περιπέτειας, ο πρωταγωνιστής Hawkeye – δεινός τοξότης – φτάνει μπροστά από τον περιστρεφόμενο ακτινωτό τροχό ενός αεραγωγού και έχει στόχο να περάσει ένα λεπτό βέλος στην άλλη πλευρά. Ο τροχός έχει οκτώ ακτινωτά ευθύγραμμα πτερύγια και κάθε ένα έχει μήκος R = 30cm. Κάθε πτερύγιο έχει σχήμα ορθογωνίου παραλληλεπιπέδου, αμελητέου πάχους και πλάτους l = 6cm, με το επίπεδό τους κάθετο στο επίπεδο του τροχού. Ο τροχός στρέφεται γύρω από σταθερό άξονα κάθετο στο επίπεδό του, με σταθερή συχνότητα f = 2,5Hz. To βέλος μήκους d = 24cm θα πρέπει να κινηθεί παράλληλα με τον άξονα περιστροφής και να διαπεράσει κάθετα το επίπεδο του τροχού, χωρίς να χτυπήσει κάποιο από τα πτερύγια. Η κίνησή του θεωρείται ευθύγραμμη ομαλή.

(α) Υπολογίστε την περίοδο και τα μέτρα της γωνιακής ταχύτητας και κεντρομόλου επιτάχυνσης ενός οποιουδήποτε σημείου της περιφέρειας του τροχού και σχεδιάστε στο σχήμα τα αντίστοιχα διανύσματα.

(β) Ποιο είναι το ελάχιστο μέτρο υ της ταχύτητας εισόδου, που πρέπει να έχει το βέλος;

(γ) Αν η αρχική απόσταση του βέλους από τον τροχό είναι s = 1,2m και τη στιγμή που εκτοξεύεται έχει απέναντί του πτερύγιο, τι θα συναντήσει φτάνοντας στον τροχό;

(δ) Έχει σημασία, πού θα περάσει οριακά το βέλος, ανάμεσα στον άξονα και την περιφέρεια του τροχού; Αν ναι, πού είναι το καλύτερο σημείο;

Απάντηση 

Παίρνουμε ένα νόμισμα των 2€ και το τοποθετούμε πάνω στο κυκλικό πλατό ενός πικάπ. Πάνω στο νόμισμα αυτό τοποθετούμε ομόκεντρα, δεύτερο νόμισμα των 10cent. Τα νομίσματα έχουν διαμέτρους δ₁ = 26mm και δ₂ = 20mm και πάχος d₁ = 2,2mm και d₂ = 2mm αντίστοιχα. Τα κέντρα των νομισμάτων και του πλατό απέχουν R = 12cm. Η πυκνότητα του κράματος κατασκευής των νομισμάτων είναι ρ = 8,5 ∙ 10³kg/m³.

Ο συντελεστής στατικής τριβής ανάμεσα στα δυο νομίσματα είναι μ_σ1 = 0,4 ενώ ανάμεσα στο δίευρο και στο πλατό είναι μ_σ2 = 0,8.

i) Υπολογίστε τη μάζα κάθε νομίσματος

ii) Βρείτε τη δύναμη που ασκείται από το πλατό στο δίευρο όταν όλα τα σώματα ηρεμούν.

iii) Αν θέσουμε το πλατό σε περιστροφή

α) σχεδιάστε τις δυνάμεις που ασκούνται στα δυο νομίσματα

β) βρείτε τη μέγιστη επιτρεπόμενη τιμή του μέτρου της γωνιακής ταχύτητας περιστροφής, για να μη γλιστράνε είτε το ένα είτε το άλλο νόμισμα.

γ) To πικάπ έχει εργοστασιακή συχνότητα περιστροφής 33στροφές /min. Μπορούμε να πετύχουμε το παραπάνω πείραμα;

Δίνεται η βαρυτική επιτάχυνση g = 10m/s².

Απάντηση 

Η περίοδος περιστροφής της Γης γύρω από τον άξονά της, ως προς τα μακρινά άστρα, που θεωρούνται ακίνητα, είναι Τ_Α και αντιστοιχεί σε 1 Αστρική Ημέρα. Το χρονικό διάστημα που μετράει ένας Γήινος παρατηρητής – κατά την διάρκεια της Ισημερίας – ως διάρκεια ενός ημερόνυχτου αντιστοιχεί σε 1 Ηλιακή Ημέρα και είναι Τ_Η = 24h. Εννοείται ότι αναφερόμαστε σε ημερόνυχτο. Είναι επίσης η χρονική διάρκεια, που απαιτείται για να ξαναδεί αυτός ο παρατηρητής τον Ήλιο την επόμενη ημέρα, στην ίδια θέση, στον ουρανό. Ένας αστροναύτης, που στέκεται πάνω από το Βόρειο Πόλο της Γης βλέπει τη Γη να στρέφεται γύρω από τον άξονά της και γύρω από τον Ήλιο αριστερόστροφα (αντιωρολογιακά) και να περιφέρεται γύρω από τον Ήλιο επίσης αντιωρολογιακά. Αν η περιφορά της Γης γύρω από το κέντρο του Ήλιου, ως προς τα μακρινά άστρα (1 Αστρικό Έτος), διαρκεί Τ = 365,25 Αστρικές Ημέρες, υπολογίστε τη χρονική διάρκεια Τ_Α μιας Αστρικής Ημέρας.

Απάντηση 

Ένα σώμα μάζας m, (πέτρα) δένεται σε ιδανικό σχοινί μήκους  L. Κάποια στιγμή ένας μαθητής θέτει το σώμα σε κατακόρυφη τροχιά ξεκινώντας από την κάτω κατακόρυφη θέση Α, όπως φαίνεται στο σχήμα 1. Αρχικά υπάρχει ένα μεταβατικό στάδιο όπου το χέρι του παιδιού δεν είναι σταθερό σε ένα σημείο ούτε η τροχιά απόλυτα κυκλική. Μετά από λίγο αποκαθίσταται κατακόρυφη κυκλική τροχιά σταθερής ακτίνας με το νήμα να είναι συνεχώς τεντωμένο και το κέντρο της τροχιάς να μπορεί να θεωρηθεί σταθερό. Αν οι δυνάμεις από τον αέρα δεν ληφθούν υπόψη ούτε υπάρχουν ελαστικές παραμορφώσεις στο σχοινί, να απαντήσετε στις ακόλουθες προτάσεις.

i)Μόλις η τροχιά του σώματος σταθεροποιηθεί το νήμα είναι:

α) Συνεχώς κάθετο με την γραμμική ταχύτητα.

Συνέχεια

σε pdf

ή σε word

Η ανάρτηση απευθύνεται στους μαθητές που αύριο θα γίνουν μηχανικοί. Είμαι σίγουρος πως αν την ξαναδούν κάποτε, θα τους φανεί το λιγότερο …απλοϊκή. Όσο πολύπλοκη όμως μηχανή και να έχουμε, πάντα θα υπακούει στους Νόμους της Μηχανικής του Newton.

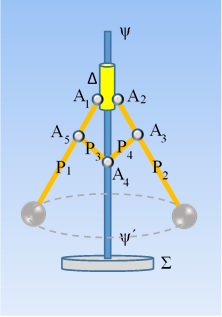
Η διάταξη του σχήματος έχει σκοπό να κινεί κατακόρυφα το δακτύλιο Δ, ο οποίος συνδέεται με βαλβίδα ρύθμισης της παροχής του ατμού στον κύλινδρο μιας ατμομηχανής. (Η βαλβίδα δεν έχει σχεδιαστεί για λόγους απλούστευσης του σχήματος, αλλά δείτε τα σχόλια στο τέλος…). Αποτελείται από την κεντρική κατακόρυφη ράβδο-άξονα ψ΄ψ, τις αβαρείς ράβδους Ρ₁ Ρ₂, Ρ₃, Ρ₄, τις αρθρώσεις Α₁, Α₂, Α₃, Α₄, Α₅, την τροχαλία Σ, προσαρμοσμένη στον άξονα ψ΄ψ και τα δύο όμοια σφαιρίδια μάζας m = 0,8kg το καθένα. Ο δακτύλιος Δ μπορεί να γλιστράει χωρίς τριβές πάνω στον άξονα ψ΄ψ.

Αν θέσουμε την τροχαλία σε περιστροφή, το σύστημα άξονας-ράβδοι-δακτύλιος, μπορεί να περιστρέφεται μαζί της, εξαιτίας της άρθρωσης Α₄, αλλά οι ράβδοι και ο δακτύλιος μπορούν να κινούνται και κατακόρυφα, με τον δακτύλιο Δ να γλιστράει πάνω στον κεντρικό άξονα ψ΄ψ.

i) Όταν αυξάνουμε τη γωνιακή ταχύτητα περιστροφής της τροχαλίας, ο δακτύλιος Δ

α) ανέρχεται.      β) κατέρχεται.    γ) δεν αλλάζει θέση κατακόρυφα.

Δικαιολογείστε την απάντησή σας.

ii) Σχεδιάστε ένα σχήμα που να φαίνεται συγκριτικά η διάταξη πριν και μετά την αύξηση της γωνιακής ταχύτητας.

iii) Αν η τροχαλία έχει ακτίνα r = 10cm, η γραμμική ταχύτητα των σημείων της περιφέρειάς της έχει μέτρο υ = 0,5m/s και η ακτίνα περιστροφής κάθε σφαιριδίου είναι R = 0,4m, ποια είναι η γωνία θ;

Απάντηση(Pdf)

O τεχνικός ενός εργοστασίου που κατασκευάζει πλυντήρια, συμμετέχοντας σε σύσκεψη, για τις προδιαγραφές των συσκευών αυτών, παρουσίασε κάποιες μετρήσεις. Ο κυλινδρικός κάδος Κ ενός μοντέλου, ακτίνας R = 0,4m περιστρέφεται με τη βοήθεια ιμάντα, που διέρχεται από το αυλάκι μιας ομοαξονικής τροχαλίας Τ₁ ακτίνας R₁ = 0,2m, προσαρμοσμένης στο πίσω μέρος του κάδου. Ο ιμάντας τίθεται σε κίνηση αφού διέρχεται και από το αυλάκι δεύτερης τροχαλίας Τ₂ ακτίνας R₂ = 0,05m, η οποία κινείται με τη βοήθεια ηλεκτρικού κινητήρα.

α) Αν το πλυντήριο στύβει τα ρούχα στις 600στροφές /min, ο τεχνικός παρουσίασε ποια είναι η γωνιακή ταχύτητα και η αντίστοιχη συχνότητα περιστροφής, για την τροχαλία Τ₂ του κινητήρα. Τι αποτελέσματα τους έδειξε;

β) Ένα στέλεχος του συμβουλίου τον ρώτησε «Γιατί τα ρούχα κολλάνε στην εσωτερική επιφάνεια του κάδου, καθώς αυτός περιστρέφεται; Πως αυτή η περιστροφή βοηθά το στέγνωμα;» Ο τεχνικός απάντησε τις ερωτήσεις και επιπλέον του είπε πόσα «G» δέχεται ένα ρούχο, εξαιτίας της γρήγορης περιστροφής και πόση δύναμη ασκεί ο κάδος σε ένα μικρό ρούχο μάζας m = 0,1kg, όταν βρίσκεται στην ανώτερη θέση κατά την περιστροφή του. Ποιες ήταν οι απαντήσεις;

γ) Ο τεχνικός παρουσίασε επίσης ότι, καθώς το στέγνωμα φτάνει στο τέλος του και η συχνότητα περιστροφής του κυλίνδρου μειώνεται, μια πλαστική σφαίρα αμελητέας ακτίνας, τοποθετημένη στον κάδο, χάνει την επαφή της, στη θέση που η επιβατική της ακτίνα σχηματίζει επίκεντρη γωνία θ = 60⁰ με την κατακόρυφη. Έτσι μπόρεσε να υπολογίσει τη συχνότητα περιστροφής εκείνη ακριβώς τη στιγμή. Πόσο λέτε ότι βρήκε;

δ) Τέλος, για ένα μικρό ρούχο μάζας m = 0,1kg, παρουσίασε τη γραφική παράσταση της αλγεβρικής τιμής της κάθετης δύναμης στήριξης από τον κάδο, σε συνάρτηση με τη γωνία θ, που σχηματίζει η επιβατική ακτίνα με την κατακόρυφο, για την γωνιακή ταχύτητα του ερωτήματος (γ). Ποια ήταν η γραφική παράσταση περιστροφή του κάδου κατά π/3 rad;

Απάντηση(Pdf)

Ένα αυτοκίνητο κινείται με σταθερό μέτρο ταχύτητας, όταν εισέρχεται σε βαθούλωμα κυκλικού σχήματος ακτίνας R₁ = 100m. Η επιτάχυνση που αισθάνεται ο οδηγός στο κατώτερο σημείο έχει μέτρο 0,4g. Στη συνέχεια εξέρχεται από το βαθούλωμα και ανέρχεται σε «σαμάρι» επίσης κυκλικού σχήματος ακτίνας R₂, στο οποίο η επιτάχυνση αποκτά μέτρο 0,25g. Δίνεται η επιτάχυνση της βαρύτητας g = 10m/s² και δεχόμαστε ότι ο οδηγός πετυχαίνει με κατάλληλη χρήση των χειριστηρίων να κρατάει το μέτρο της ταχύτητας συνεχώς σταθερό.

α) Ποιο είναι το μέτρο της ταχύτητας του αυτοκινήτου και η ακτίνα R₂; Σχεδιάστε τα διανύσματα των επιταχύνσεων του αυτοκινήτου, καθώς διέρχεται από το κατώτερο σημείο του βαθουλώματος και το ανώτερο σημείο του υψώματος.

β) Αν οι επίκεντρες γωνίες των δυο διαδρομών είναι Δθ = =120⁰ ποια είναι η χρονική διάρκεια που θα χρειαστεί το αυτοκίνητο να περάσει από τις δυο περιοχές;

γ) Αν η μάζα του αυτοκινήτου είναι m = 800kg, πόση  είναι η κάθετη αντίδραση που δέχεται το αυτοκίνητο από το δρόμο στο κατώτερο σημείο του βαθουλώματος και στο ανώτερο σημείο του υψώματος;

δ) Παρατηρώντας τα αποτελέσματα της ερώτησης (γ) μπορείτε να προβλέψετε σε ποια από τις δύο θέσεις είναι δυνατόν να χαθεί η επαφή με το δρόμο; Με ποια ταχύτητα του αυτοκινήτου θα συνέβαινε αυτό;

Απάντηση(Pdf)