Η ράβδος περιστρέφεται, αναγκάζοντας τη μπάλα να κινείται με σταθερή ταχύτητα μέτρου υ, σε έναν οριζόντιο κύκλο ακτίνας R. Τα νήματα έχουν το καθένα μήκος L συνδέονται τη ράβδο με δακτυλίους που περιστρέφονται ελεύθερα χωρίς τριβές γύρω από τη ράβδο. Κάθε νήμα είναι τεντωμένο και σχηματίζει γωνία θ με την κατακόρυφο.
α) Σχεδιάστε στη σφαίρα τις δυνάμεις και το διάνυσμα της κεντρομόλου επιτάχυνσης.
β) Πάρτε πάνω στη σφαίρα ένα σύστημα ορθογωνίων αξόνων Χ΄X οριζόντιο και Ψ΄Ψ κατακόρυφο και γράψτε τις δύο εξισώσεις στο S.I., που προκύπτουν από την εφαρμογή του δεύτερου νόμου του Νεύτωνα στη σφαίρα, για κάθε άξονα. Δίνονται: m = 3kg, L = 1,60m, θ = 60° , g = 10m/s2 και υ = 8 m/s.
γ) Βρείτε το μέτρο κάθε τάσης νήματος. Ήταν αναμενόμενο το αποτέλεσμα;




 Υλικό σημείο Ρ κινείται ευθύγραμμα και ομαλά με σταθερή ταχύτητα υ. Την κίνηση παρακολουθεί παρατηρητής, που βρίσκεται στην αρχή Ο του συστήματος ΧΟΨ ορθογωνίων αξόνων, που φαίνεται στο παρακάτω σχήμα.
Υλικό σημείο Ρ κινείται ευθύγραμμα και ομαλά με σταθερή ταχύτητα υ. Την κίνηση παρακολουθεί παρατηρητής, που βρίσκεται στην αρχή Ο του συστήματος ΧΟΨ ορθογωνίων αξόνων, που φαίνεται στο παρακάτω σχήμα. Μια σφαίρα εκτοξεύεται οριζόντια από σημείο Ο της ταράτσας ενός κτιρίου ύψους Η = 25m. Από τη βάση Β του κτιρίου ξεκινάει μια κεκλιμένη ράμπα, γωνίας κλίσης θ = 300. Η σφαίρα προσκρούει κάθετα στη ράμπα στο σημείο Α, όπως φαίνεται στο σχήμα.
Μια σφαίρα εκτοξεύεται οριζόντια από σημείο Ο της ταράτσας ενός κτιρίου ύψους Η = 25m. Από τη βάση Β του κτιρίου ξεκινάει μια κεκλιμένη ράμπα, γωνίας κλίσης θ = 300. Η σφαίρα προσκρούει κάθετα στη ράμπα στο σημείο Α, όπως φαίνεται στο σχήμα.
 Παίρνουμε ένα νόμισμα των 2€ και το τοποθετούμε πάνω στο κυκλικό πλατό ενός πικάπ. Πάνω στο νόμισμα αυτό τοποθετούμε ομόκεντρα, δεύτερο νόμισμα των 10cent. Τα νομίσματα έχουν διαμέτρους δ1 = 26mm και δ2 = 20mm και πάχος d1 = 2,2mm και d2 = 2mm αντίστοιχα. Τα κέντρα των νομισμάτων και του πλατό απέχουν R = 12cm. Η πυκνότητα του κράματος κατασκευής των νομισμάτων είναι ρ = 8,5 ∙ 103kg/m3.
Παίρνουμε ένα νόμισμα των 2€ και το τοποθετούμε πάνω στο κυκλικό πλατό ενός πικάπ. Πάνω στο νόμισμα αυτό τοποθετούμε ομόκεντρα, δεύτερο νόμισμα των 10cent. Τα νομίσματα έχουν διαμέτρους δ1 = 26mm και δ2 = 20mm και πάχος d1 = 2,2mm και d2 = 2mm αντίστοιχα. Τα κέντρα των νομισμάτων και του πλατό απέχουν R = 12cm. Η πυκνότητα του κράματος κατασκευής των νομισμάτων είναι ρ = 8,5 ∙ 103kg/m3.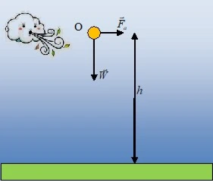
 Μια άσκηση του Πυροβολικού, εξελίσσεται σε περιοχή με μορφολογία που φαίνεται στο σχήμα 1. Το πυροβόλο βρίσκεται στην κορυφή του λόφου ύψους h1 = 20m πάνω από την επιφάνεια λίμνης και εκτοξεύει οριζόντια βλήματα μάζας m = 10kg. Τα βλήματα πρέπει να περάσουν τη λίμνη, που βρίσκεται στο οροπέδιο και να πέσουν στην πεδιάδα, που βρίσκεται σε απόσταση h2 = 25m κάτω από την επιφάνεια της λίμνης.
Μια άσκηση του Πυροβολικού, εξελίσσεται σε περιοχή με μορφολογία που φαίνεται στο σχήμα 1. Το πυροβόλο βρίσκεται στην κορυφή του λόφου ύψους h1 = 20m πάνω από την επιφάνεια λίμνης και εκτοξεύει οριζόντια βλήματα μάζας m = 10kg. Τα βλήματα πρέπει να περάσουν τη λίμνη, που βρίσκεται στο οροπέδιο και να πέσουν στην πεδιάδα, που βρίσκεται σε απόσταση h2 = 25m κάτω από την επιφάνεια της λίμνης.
