Ιδανικό αέριο υποβάλλεται στην κυκλική μεταβολή ΑΒΓΔΕΖΓΗΑ του σχήματος. Οι δύο καμπύλες έχουν σχήμα κύκλου με ακτίνες R₁ > R₂.

i) Κατά τη διάρκεια της πλήρους κυκλικής μεταβολής το αέριο παράγει

α) Θετικό έργο                          β) Αρνητικό έργο                      γ) Μηδενικό έργο

Βρείτε τη σωστή απάντηση και δικαιολογείστε την.

ii) Στην κυκλική αυτή μεταβολή η συνολική θερμότητα, που ανταλλάσσει το αέριο εισρέει ή αποβάλλεται από το σύστημα; Εξηγείστε.

iii) Θα μπορούσε να χρησιμοποιηθεί αυτός ο κύκλος από μια θερμική μηχανή; Εξηγείστε.

Απάντηση 

Απάντηση 

Μια θερμική μηχανή Carnot C₁, προσλαμβάνει θερμότητα από μια δεξαμενή θερμοκρασίας θ_h1 = 727⁰C με ρυθμό P_h1 = 6kW και αποβάλλει θερμότητα στο περιβάλλον, που έχει θερμοκρασία Τ_c1 = 300K. Η μηχανική ισχύς που παράγει η θερμική μηχανή χρησιμοποιείται για να τροφοδοτήσει ένα ψυγείο Carnot C₂ . Τι κάνει το ψυγείο; Αφαιρεί θερμότητα από το χώρο ψύξης ο οποίος έχει έτσι θερμοκρασία θ_c2 = -13⁰C και την αποβάλλει στο περιβάλλον που έχει θερμοκρασία Τ_h2 = 300K. Αφού σχεδιάσετε τις δυο μηχανές, υπολογίστε:

α) Την απόδοση της θερμικής μηχανής C₁ και τη μηχανική ισχύ P₁, που προσφέρει στο ψυγείο.

β) Ποιος είναι ο συντελεστής λειτουργίας του ψυγείου C₂.

γ) Το ρυθμό με τον οποίο αφαιρείται θερμότητα από το χώρο ψύξης στην C₂.

δ) Το ρυθμό με τον οποίο αποβάλλεται θερμότητα στο περιβάλλον από το ψυγείο C₂.

ε) Το συνολικό ρυθμό αποβολής θερμότητας στο περιβάλλον του συστήματος των δυο μηχανών.

Απάντηση 

Απάντηση 

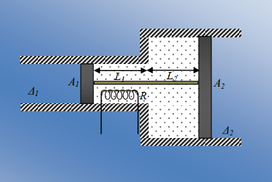Τα τοιχώματα των δύο ενωμένων κυλινδρικών δοχείων Δ₁, Δ₂ του σχήματος είναι αδιαβατικά (θερμομονωτικά). Οι εγκάρσιες διατομές των κυλίνδρων είναι Α₁ =1∙10^-1m², A₂ = 4∙10^-1m² αντίστοιχα. Σε κάθε δοχείο υπάρχει από ένα έμβολο καλά εφαπτόμενο στα τοιχώματα, αλλά ελεύθερα κινούμενο, χωρίς τριβές, σε αποστάσεις L₁ = L₂ = L = 1,5∙10^-1m από το σημείο που αλλάζει η εγκάρσια διατομή. Τα έμβολα συνδέονται μεταξύ τους με πολύ λεπτή αβαρή ράβδο. Στον κλειστό χώρο που δημιουργείται, ανάμεσα στα έμβολα, υπάρχει ιδανικό αέριο σε θερμοκρασία Τ₀ = 300Κ. Η πίεση του αερίου είναι ίση με την εξωτερική ατμοσφαιρική δηλαδή p₀ = p_atm = 10⁵Pa.

α) Ποιο είναι το μέτρο της δύναμης, που ασκεί σε κάθε έμβολο η ράβδος σύνδεσης, στην αρχική κατάσταση ισορροπίας;

Αφήνουμε για χρονικό διάστημα Δt = 2min, να διέλθει ηλεκτρικό ρεύμα από τον αντιστάτη R, ο οποίος έχει ισχύ P = 30W.

β) Ποιο είναι το είδος της μεταβολής που υφίσταται το αέριο;

γ) Σε ποια κατεύθυνση θα μετακινηθούν τα έμβολα και γιατί;

δ) Ποια θα είναι η μετατόπιση των εμβόλων, μέχρι η νέα κατάσταση ισορροπίας να πραγματοποιηθεί;

ε) Ποια θα είναι η τελική θερμοκρασία του αερίου;

Απάντηση 

Απάντηση 

Ένα εξωγήινο εξερευνητικό σκάφος μπαίνει στην ατμόσφαιρα της Αφροδίτης. Στο σκάφος λειτουργεί μια μηχανή Carnot μεταξύ δύο δεξαμενών θερμότητας σε θερμοκρασίες Τ_h = 1200 K και T_c = 300 K. Κάποια στιγμή, που μπορούμε να θεωρήσουμε t₀ = 0s, λόγω βλάβης, η θερμοκρασία T_c αρχίζει να αυξάνεται με ρυθμό  dT_c/dt = 0,5K/s.

α) Ποια σχέση δίνει τo συντελεστή απόδοσης της θερμικής μηχανής σε συνάρτηση με το χρόνο;

β) Να κάνετε τη γραφική παράσταση του συντελεστή απόδοσης σε συνάρτηση με το χρόνο, από t₀ = 0s, ως t = 350s.

γ) Από το εξωγήινο κέντρο ελέγχου διαπιστώνουν ότι θα μπορούσαν να κρατήσουν σταθερό το συντελεστή απόδοσης, αν αυξάνεται η θερμοκρασία της θερμής δεξαμενής.

Μπορούν να επιτύχουν το εγχείρημα με γραμμική αύξηση της θερμοκρασίας της θερμής δεξαμενής; Αν ναι ποιος θα είναι ο ρυθμός μεταβολής αυτής της θερμοκρασίας;

Απάντηση 

Απάντηση 

Ο Ερμής είναι ο πλησιέστερος πλανήτης στον Ήλιο. Αυτό δημιουργεί ένα μεγάλο πρόβλημα αν θέλουμε να δημιουργήσουμε αποικία, αφού την ημέρα η θερμοκρασία είναι 430⁰C και το βράδυ πέφτει στους -180⁰C. Οι άποικοι φυσικά θα πρέπει να ζουν σε θόλους με κλιματισμό. Ας θεωρήσουμε ότι ένα κλιματιστικό μηχάνημα, λειτουργεί σαν ιδανική μηχανή Carnot και στο χώρο διαβίωσης δημιουργεί θερμοκρασία 20⁰C. Ο ρυθμός απώλειας ενέργειας από ή προς το περιβάλλον από τη μόνωση του θόλου είναι 0,5KJ/s για διαφορά θερμοκρασίας 1⁰C .

α) Ποιος είναι ο ρυθμός  απώλειας ενέργειας τη νύχτα και ποια η ισχύς της μηχανής Carnot, όταν λειτουργεί κατά τη διάρκεια της νύχτας;

β) Ποιος είναι ο ρυθμός  εισροής ενέργειας την ημέρα και ποια η ισχύς της μηχανής Carnot, όταν λειτουργεί κατά τη διάρκεια της ημέρας;

Απάντηση(Word)

Απάντηση(Pdf)

Το ιδανικό μονοατομικό αέριο μιας θερμικής μηχανής υποβάλλεται στην κυκλική μεταβολή που φαίνεται στο διπλανό διάγραμμα  P→V, όπου 1→2 είναι ισόθερμη εκτόνωση, 2→3 είναι ισόχωρη ψύξη, 3→4 είναι ισόθερμη συμπίεση και 4→1 είναι ισόχωρη θέρμανση μέχρι την αρχική κατάσταση. Να υπολογίσετε το θερμοδυναμικό συντελεστή απόδοσης της μηχανής και να τον συγκρίνετε με αυτόν της μηχανής Carnot, που εργάζεται ανάμεσα στις ίδιες θερμοκρασίες.

ΣΥΝΕΧΕΙΑ