Κατηγορία: 3. ΦΥΣΙΚΗ Β΄ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ

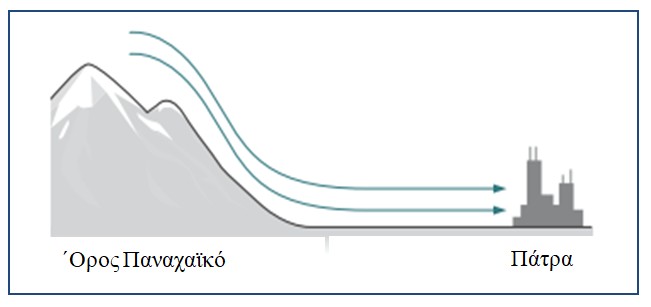Ο ανατολικός άνεμος συχνά μεταφέρει αέρα από ψηλά στο Παναχαϊκό, μέχρι την Πάτρα, αρκετά γρήγορα ώστε ο αέρας δεν έχει χρόνο για ανταλλαγή θερμότητας με το περιβάλλον του. Έστω ότι κάποια μέρα, η θερμοκρασία και η πίεση στην κορυφή του Παναχαϊκού είναι Τ₁ = 270Κ (-3⁰C) και p₁ = 75kPa αντίστοιχα. Η πίεση στην πόλη παρακάτω είναι p₂ = 100kPa. Να βρείτε τη σωστή απάντηση στις παρακάτω προτάσεις, δικαιολογώντας την επιλογή σας.

i) Η διαδικασία που υφίσταται ο αέρας καθώς κατεβαίνει τα βουνά είναι

α) ισόθερμη                  β) ισόχωρη                    γ) ισοβαρής                   δ) αδιαβατική

ii) Όταν ο αέρας φτάσει στην πεδιάδα, η θερμοκρασία του είναι περίπου

α) -15 ⁰C                       β) 10 ⁰C                        γ) 16 ⁰C                        δ) 30 ⁰C

Δίνεται γ = 1,3

iii) Καθώς ο αέρας κατεβαίνει, ο όγκος του

α) αυξάνεται κατά 50%

β) αυξάνεται λιγότερο από 50%

γ) μειώνεται κατά 50%

δ) μειώνεται λιγότερο από 50%

ε) παραμένει σταθερός

iv) Καθώς ο αέρας κατεβαίνει, η εσωτερική του ενέργεια

α) αυξάνεται                  β) μειώνεται                  γ) παραμένει σταθερή

v) Η μάζα αυτή του κινούμενου αέρα

α) παίρνει ενέργεια

β) δίνει ενέργεια

γ) δεν ανταλλάσσει ενέργεια με το περιβάλλον της.

vi) Να κάνετε μια ποιοτική γραφική παράσταση p – V, βαθμολογώντας μόνο τον άξονα των p.

Απάντηση 

Απάντηση 

Ο μεταλλικός κύλινδρος του σχήματος έχει την πάνω βάση του κλειστή και την κάτω ανοιχτή. Τον κρατάμε σε κατακόρυφη θέση, ώστε η κάτω βάση να εφάπτεται στην ήρεμη επιφάνεια του νερού μιας πισίνας. Το ύψος του κυλίνδρου είναι h = 1,1m και περιέχει αέρα που θεωρείται ιδανικό αέριο. Βυθίζουμε αργά όλο τον κύλινδρο στο νερό. Παρατηρούμε ότι μια ποσότητα νερού εισχωρεί μέχρι κάποιο ύψος εντός του κυλίνδρου και όταν επέλθει ισορροπία, ο εγκλωβισμένος αέρας γεμίζει μια κυλινδρική περιοχή σε βάθος y από την πάνω βάση.

α) Υπολογίστε την τιμή του y. Η μεταβολή θεωρείται ισόθερμη, η ατμοσφαιρική πίεση είναι p_atm = 10⁵N/m², η πυκνότητα του νερού ρ = 10 kg/m³ και η βαρυτική επιτάχυνση g = 10m/s².

β) Να κάνετε τη γραφική παράσταση p – V σε βαθμολογημένους άξονες,  αν η διάμετρος της βάσης του κυλίνδρου είναι δ = 0,8/√π m.

γ) Αν δίνεται ότι το πάχος του μετάλλου x = 5mm και η πυκνότητα του υλικού του ρ₁ = 2700kg/m³(αλουμίνιο), πόση δύναμη πρέπει να ασκηθεί για να κρατήσουμε τον κύλινδρο βυθισμένο;

δ) Στην ταινία “Πειρατές της Καραϊβικής” ο Τζακ Σπάροου βρίσκει τρόπο να γλυτώσει με την αντεστραμμένη βάρκα, που φαίνεται στην εικόνα, που όπως και στην περίπτωσή μας εγκλωβίζει αέρα και έτσι μπορούν να αναπνέουν κάτω από το νερό. Σχολιάστε τη σκηνή.

Απάντηση 

Απάντηση 

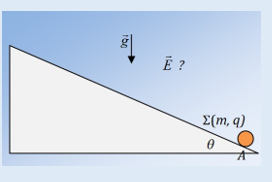Ένα μικρό σώμα μάζας Σ, μάζας m = 0,3√3kg και φορτίου q = 5mC βρίσκεται ακίνητο σε σημείο Α λείου κεκλιμένου επιπέδου γωνίας θ =30°. Στο χώρο, εκτός από το (ομογενές) βαρυτικό πεδίο της Γης, μέτρου έντασης  g = 10Ν/kg, υπάρχει και οριζόντιο ομογενές ηλεκτρικό πεδίο έντασης Ε , άγνωστης φοράς.

α. Να υπολογίσετε την ένταση του ηλεκτρικού πεδίου (μέτρο και κατεύθυνση) ώστε το σώμα να παραμείνει ακίνητο.

Τριπλασιάζουμε το μέτρο της έντασης του ηλεκτρικού πεδίου, χωρίς να αλλάξουμε τη φορά της.

β. Υπολογίστε το μέτρο της επιτάχυνσης που αποκτά το σώμα κατά μήκος του κεκλιμένου επιπέδου.

γ. Με ποια ταχύτητα θα φτάσει το σώμα στο σημείο Β, που βρίσκεται σε ύψος h = 2,5m πάνω από το σημείο Α;

δ. Τη χρονική στιγμή που το σώμα διέρχεται από το σημείο Β βρείτε:

δ1. το ρυθμό μεταβολής κινητικής ενέργειας

δ2. το ρυθμό μεταβολής βαρυτικής δυναμικής ενέργειας

δ3. το ρυθμό μεταβολής ηλεκτρικής δυναμικής ενέργειας

και επαληθεύστε την Αρχή Διατήρησης της Μηχανικής Ενέργειας.

Απάντηση 

Απάντηση 

Μεταλλική σφαίρα Σ₁ με φορτίο Q = -1mC και ακτίνα R = 0,2m είναι στερεωμένη σε χώρο που έχει αφαιρεθεί ο αέρας και επικρατούν συνθήκες έλλειψης βαρύτητας. Δίνεται k_c = 9∙10⁹Nm²/C²

α) Με ποιο ελάχιστο μέτρο αρχικής ταχύτητας πρέπει να εκτοξεύσουμε μικρή σφαίρα Σ₂ μάζας m = 0,2kg και φορτίου q = +1μC , που βρίσκεται σε απόσταση h = 0,7m από την επιφάνεια της σφαίρας Σ₁ για να διαφύγει από το ηλεκτρικό πεδίο της; Τι κίνηση θα εκτελέσει η σφαίρα Σ₂;

β) Σε ποια κατεύθυνση και με ποιο μέτρο ταχύτητας πρέπει να εκτοξευτεί η σφαίρα Σ₂ ώστε να μπει σε κυκλική τροχιά γύρω από το κέντρο της σφαίρας Σ₁ – να γίνει δηλαδή δορυφόρος της σφαίρας Σ₁;

Απάντηση 

Διαστημικό όχημα Ο, με μάζα M = 4000kg, που μεταφέρει άκατο διαφυγής  μάζας m = 1000kg, περιφέρεται ως δορυφόρος κυκλικής τροχιάς γύρω από τη Γη σε ύψος h = 3R_Γ από την επιφάνειά της (R_Γ  = 6400km η ακτίνα της Γης). Κάποια στιγμή το διαστημικό όχημα ελευθερώνει την άκατο Α με τέτοιο τρόπο ώστε η ταχύτητά της ως προς τη Γη, να είναι μηδέν. Η άκατος αρχίζει τότε να κατεβαίνει προς τη Γη εκτελώντας ευθύγραμμη κίνηση και φτάνει στην επιφάνειά της με την κατάλληλη χρήση ανασχετικών πυραύλων, έχοντας ταχύτητα μηδέν.

α. Υπολογίστε την ταχύτητα του οχήματος Ο, πριν την διάσπαση.

β. Να εξηγήσετε γιατί η απελευθέρωση της ακάτου πρέπει να γίνει με εκτόξευση της ακάτου αντίθετα από την κατεύθυνση της ταχύτητας του σταθμού

γ. Να υπολογιστεί η ταχύτητα του διαστημικού οχήματος αμέσως μετά την αποβολή της ακάτου και να εξετάσετε αν είναι δυνατόν το όχημα να διαφύγει από την έλξη της Γης.

δ. Να υπολογιστεί το έργο της δύναμης των ανασχετικών πυραύλων.

ε. Με πόση ταχύτητα θα χτυπούσε στην επιφάνεια της Γης, αν δεν λειτουργούσαν οι ανασχετικοί πύραυλοι;

Η Γη θεωρείται ακίνητη, χωρίς ατμόσφαιρα, η επιτάχυνση της βαρύτητας στην επιφάνεια της Γης είναι g_ο= 10m/s² και αγνοούμε την επίδραση άλλων σωμάτων, πλην της Γης.

Απάντηση 

Απάντηση 

Το 1959 ο Ρώσος μηχανικός Yuri N. Artsutanov, τροποποιώντας μια ιδέα του επίσης Ρώσου μηχανικού ρουκετών Konstantin Tsiolkovsky, σκέφτηκε να κατασκευάσουμε έναν διαστημικό ανελκυστήρα, όπως στο σχήμα 1. (Το σχήμα αυτό δείχνει την κάτοψη της Γης καθώς τη βλέπουμε ακριβώς πάνω από το Βόρειο Πόλο). Δηλαδή να συνδέσουμε με νήμα ένα σημείο Σ στον Ισημερινό της Γης με έναν γεωστατικό δορυφόρο Δ. Πάνω σε αυτό το νήμα θα κινείται η καμπίνα του ανελκυστήρα. Για να διερευνήσουμε κάποιες από τις προϋποθέσεις της ιδέας:
α) Ας υπολογίσουμε το ύψος από την επιφάνεια της Γης που πρέπει να τοποθετηθεί ένας γεωστατικός δορυφόρος.
β) Αν δεχτούμε το νήμα αβαρές(!), ποια θα είναι η τάση του νήματος; Τι συμπεραίνουμε;
γ) Η απάντηση στο ερώτημα (β) δείχνει ότι απαιτείται η τοποθέτηση ενός αντίβαρου Α. Αν τοποθετηθεί σε απόσταση d = 100000km από το κέντρο της Γης,
i) ποιο θα είναι το μέτρο της βαρυτικής έλξης της Γης στο δορυφόρο και στο αντίβαρο αν έχουν την ίδια μάζα m = 10000kg;
ii) ποια θα είναι τα μέτρα των τάσεων των δύο νημάτων που θα χρησιμοποιηθούν αν θεωρηθούν αβαρή(!);
δ) Η Ιαπωνική εταιρεία Obayashi υποσχέθηκε ότι μέχρι το 2050 θα έχει κατασκευάσει το διαστημικό ανελκυστήρα. Η καμπίνα θα κινείται κατά μήκος του νήματος με σταθερή ταχύτητα μέτρου 200km/h. Πόσο χρόνο θα χρειάζεται για να φτάσει στη γεωστατική τροχιά και στο αντίβαρο;
ε) Ένας επιβάτης του ανελκυστήρα καταγράφει με τη βοήθεια μιας ζυγαριάς το βάρος του. Να κάνετε τη γραφική παράσταση των μετρήσεων που θα πάρει μέχρι να φτάσει στο αντίβαρο.
στ) Το αβαρές νήμα φυσικά δεν υπάρχει. Ακριβείς υπολογισμοί δίνουν την τάση του νήματος στο γεωστατικό δορυφόρο …

Συνέχεια (Pdf)

Ένας τεχνητός δορυφόρος της Γης, σε κυκλική τροχιά κοντά στην επιφάνειά της, χρειάζεται περίπου 84 λεπτά ανά περιστροφή. Ένας τεχνητός δορυφόρος της Σελήνης, σε κυκλική τροχιά κοντά στην επιφάνειά της, θέλει περίπου 108 λεπτά ανά περιστροφή.

Τι μπορείτε να συμπεράνετε για την πυκνότητα της Σελήνης και της Γης;

α) ρ_Σ = ρ_Γ         β) ρ_Σ > ρ_Γ         γ) ρ_Σ < ρ_Γ

Δικαιολογείστε την απάντησή σας.

Απάντηση 

Απάντηση 

Ας υποθέσουμε ότι η Γη και η Σελήνη είναι ακίνητες και τα μοναδικά σώματα στο διάστημα, ώστε να σχεδιάσουμε μια αποστολή στη Σελήνη. Ένα μη επανδρωμένο διαστημόπλοιο μάζας m = 200kg, με εξελιγμένους κινητήρες ιόντων θα έχει σταθερή επιτάχυνση μέτρου |α| = 0,1m/s² μέχρι το σημείο που η ένταση του πεδίου βαρύτητας μηδενίζεται και σταθερή επιβράδυνση για την υπόλοιπη διαδρομή, μέχρι να σταματήσει φτάνοντας στη Σελήνη. Η απόσταση κέντρο Γης – κέντρο Σελήνης είναι περίπου d = 4∙10⁸m και η διαδρομή θα είναι η πιο σύντομη, δηλαδή ευθεία. Οι μάζες Γης και Σελήνης έχουν σχέση Μ_Γ = 81Μ_Σ.

α) Σε ποιο σημείο Σ της διαδρομής πρέπει να αρχίσει η επιβράδυνση του διαστημοπλοίου;

β) Ποιο είναι το μέτρο της μέγιστης ταχύτητας που αποκτά το διαστημόπλοιο και πόσο χρόνο διαρκεί το ταξίδι;

γ) Υπολογίστε την ταχύτητα διαφυγής από το βαρυτικό πεδίο της Γης, αν δίνονται η ακτίνα της Γης R_Γ = 6400km και η ένταση του βαρυτικού της πεδίου στην επιφάνεια g₀ = 10N/kg. Καταφέρνει το διαστημόπλοιο να την «πιάσει»; Αν η απάντηση στο ερώτημα είναι όχι, πως καταφέρνει να φτάσει στη Σελήνη; Μήπως δε χρειάζεται να αποκτήσει ταχύτητα διαφυγής;

δ) Πόση ενέργεια θα χρειαστεί για αυτή την αποστολή;

ε) Αναζητείστε στο διαδίκτυο πόσο χρόνο διαρκεί ένα πραγματικό ταξίδι από τη Γη στη Σελήνη και πόση ενέργεια χρειαζόμαστε. Γιατί διαφέρουν τόσο πολύ από τα αποτελέσματα της άσκησης;

Απάντηση 

Απάντηση 

Διαστημικός σταθμός περιστρέφεται σε ελλειπτική τροχιά γύρω από τη Γη, με ελάχιστη και μέγιστη απόσταση από το κέντρο της  r₁= 7∙10⁶m  και r₂= 9∙10⁶m,  αντίστοιχα.  Αν η ταχύτητά του όταν βρίσκεται σε απόσταση r₁ (ελάχιστη) είναι υ₁ = 8∙10³m/s, να υπολογιστούν:

α) Η ταχύτητά του όταν βρίσκεται σε απόσταση r₂ (μέγιστη).

β) Η ελάχιστη ενέργεια που πρέπει να προσφερθεί σε μια συσκευή, μάζας m = 140 kg, που βρίσκεται στο διαστημικό σταθμό, για να φτάσει στο άπειρο. Δικαιολογήστε γιατί η ενέργεια αυτή είναι ίδια από οποιοδήποτε σημείο της ελλειπτικής τροχιάς και αν πραγματοποιηθεί η βολή.

Δίνονται η ακτίνα της Γης R_Γ = 6400km και η ένταση του πεδίου βαρύτητας στην επιφάνεια της Γης g_ο = 10m/s²

Απάντηση 

Απάντηση