Είστε ειδικός αναλυτής για την Εθνική Ασφάλεια Μεταφορών (ΕΑΜ) και κάνετε έρευνα για ένα ατύχημα στο μετρό. Ένα τρένο Τ₁ κινούμενο με ταχύτητα μέτρου υ₁ = 90km/h συγκρούστηκε με ένα πιο αργό τρένο Τ₂, που ταξίδευε στην ίδια κατεύθυνση με ταχύτητα μέτρου υ₂ = 36km/h. Η δουλειά σας είναι να προσδιορίσετε τη διαφορά των ταχυτήτων των τρένων τη στιγμή της σύγκρουσης και να προτείνετε τη θέσπιση νέων προτύπων ασφάλειας… Το τρένο Τ₁ έχει «μαύρο κουτί», που έδειξε ότι πατήθηκαν τα φρένα του και άρχισε να επιβραδύνεται ομαλά με ρυθμό |α| = 2m/s² όταν βρισκόταν σε απόσταση d = 50m από το τρένο Τ₂, το οποίο συνέχιζε με σταθερή ταχύτητα. Θεωρούμε τα τρένα υλικά σημεία.

i) Πόσο χρονικό διάστημα, μετά από τη στιγμή – έστω t₀ = 0s – που πατήθηκαν τα φρένα του Τ₁, χρειάστηκε για να γίνει η σύγκρουση;

ii) Να κάνετε τη γραφική παράσταση της θέσης κάθε τρένου σε συνάρτηση του χρόνου στο ίδιο σύστημα αξόνων, με πεδίο ορισμού 0s ≤ t ≤ 12s.

iii) Να κάνετε τη γραφική παράσταση της ταχύτητας κάθε τρένου σε συνάρτηση του χρόνου στο ίδιο σύστημα αξόνων, μέχρι τη χρονική στιγμή της σύγκρουσης.

iv) Τι θα γράφατε στην αναφορά για το ατύχημα;

Απάντηση 

Ένα κλειστό γυάλινο κυλινδρικό δοχείο, μάζας Μ = 200g, ισορροπεί ακίνητο πάνω στον οριζόντιο δίσκο ευαίσθητης ζυγαριάς, βαθμολογημένης σε Ν. Η ένδειξη της ζυγαριάς είναι 1,96 Ν.

i) Ποια δύναμη μετράει η ζυγαριά;
ii) Ποια είναι η επιτάχυνση της βαρύτητας στον τόπο που γίνεται το πείραμα;
iii) Αν μέσα στο δοχείο βρίσκεται κλεισμένη μια (μάλλον μεταλλαγμένη) μύγα μάζας m = 1g, κάποια στιγμή που η μύγα αιωρείται και ισορροπεί,
iiia) ποιο είναι το μέτρο της δύναμης που ασκείται στον αέρα του δοχείου, από τα φτερά της μύγας;
iiib) η ένδειξη της ζυγαριάς είναι
α) ίση με 1,96Ν             β) μικρότερη από 1,96Ν             γ) μεγαλύτερη από 1,96Ν
iv) Αν μέσα στο δοχείο βρίσκονται 100 μύγες, που πετάνε προς τυχαίες διευθύνσεις, η ένδειξη της ζυγαριάς είναι
α) ίση με 1,96Ν             β) μικρότερη από 1,96Ν             γ) μεγαλύτερη από 1,96Ν

Απάντηση 

Απάντηση 

Δυο σώματα Σ1 και Σ2 ίδιας μάζας, δένονται στα άκρα ενός αβαρούς μη εκτατού νήματος, που περνά από μια αβαρή τροχαλία. Αρχικά, το σύστημα βρίσκεται σε ηρεμία και τα σώματα  βρίσκονται στο ίδιο κατακόρυφο επίπεδο. Εκτοξεύουμε το σώμα Σ2 με οριζόντια ταχύτητα στο επίπεδο του σχήματος. Το σώμα Σ2 λίγο μετά:

α. βρίσκεται σε υψηλότερο οριζόντιο επίπεδο από το Σ1.

β. βρίσκεται σε χαμηλότερο οριζόντιο επίπεδο από το Σ1.

γ. βρίσκεται στο ίδιο οριζόντιο επίπεδο με το Σ1.

Απάντηση 

Απάντηση 

 

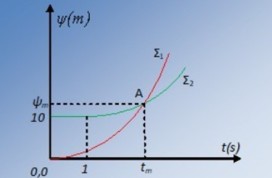Το διάγραμμα θέσης – χρόνου αναφέρεται σε δύο μικρές σφαίρες Σ₁ και Σ₂, με μάζες m₁ και m₂ > m₁,  που βρίσκονται στο ίδιο κατακόρυφο επίπεδο και αφήνονται να εκτελέσουν ελεύθερη πτώση, απουσία αέρα, παράλληλα σε έναν κατακόρυφο άξονα Ψ΄Ψ, με θετική φορά προς τα κάτω. Η επιτάχυνση της βαρύτητας έχει μέτρο g = 10m/s².

α) Ποιες είναι οι αρχικές συνθήκες (t₀₁, ψ₀₁, t₀₂, ψ₀₂) εκτέλεσης του πειράματος; Σχεδιάστε έναν βαθμολογημένο άξονα Ψ΄Ψ, και τοποθετήστε σχετικά με αυτόν τις σφαίρες τη χρονική στιγμή t = 0, σχεδιάζοντας και τις δυνάμεις, που ασκούνται.
β) Γράψτε τις εξισώσεις θέσης – χρόνου των σφαιρών στο S.I.
γ) Τι εκφράζουν οι συντεταγμένες του σημείου τομής Α των δύο γραφικών παραστάσεων; Υπολογίστε τις τιμές t_m και ψ_m.
δ) Να γράψετε τη χρονική εξίσωση που δίνει κάθε στιγμή την απόσταση των δύο σφαιρών και να κάνετε την αντίστοιχη γραφική παράσταση σε βαθμολογημένους άξονες.
στ) Πότε η απόσταση των σφαιρών θα γίνει d = 20m;

Απάντηση 

Απάντηση 

Μια άσκηση, του Θοδωρή Παπασγουρίδη.

Ο κακός λύκος είναι πολύ πεινασμένος. Για καλή του τύχη βλέπει ένα άτακτο κατσικάκι που έχει φύγει από τη μαμά του. Δυστυχώς όμως για το λύκο, τη στιγμή που βλέπει το κατσικάκι και το κατσικάκι βλέπει το λύκο. Ο λύκος, το κατσικάκι και το μαντρί βρίσκονται στην ίδια ευθεία. Το μαντρί βρίσκεται ανάμεσα στο λύκο και το κατσικάκι. Ο λύκος απέχει d₁ = 120m από το μαντρί ενώ το κατσικάκι d₂ = 75m. Ο πεινασμένος λύκος ακαριαία μόλις βλέπει το κατσικάκι αρχίζει να τρέχει προς αυτό, τη χρονική στιγμή t₀₁ = 0. Ο λύκος μπορεί να αναπτύξει σταθερή επιτάχυνση α₁=3m/s² για χρονικό διάστημα Δt₁=4s. Στη συνέχεια μπορεί να κινείται με σταθερή ταχύτητα ίση με αυτή που ανέπτυξε στο χρονικό διάστημα Δt₁=4s. Το κατσικάκι σάστισε και για 2s έμεινε ακίνητο από το φόβο του. Τελικά αποφάσισε να τρέξει προς το μαντρί.

Θεωρείστε έναν άξονα x΄x με αρχή το σημείο που βρίσκεται ο λύκος τη χρονική στιγμή t = 0 και θετική φορά από το λύκο προς το κατσικάκι.

α) Τι κίνηση εκτελεί κάθε ζώο;

β) Ποια χρονική στιγμή θα φτάσει ο λύκος στο μαντρί;

γ) Ποια είναι η ελάχιστη τιμή του μέτρου της επιτάχυνσης, που πρέπει να αναπτύξει το κατσικάκι, ώστε να φτάσει έγκαιρα στο μαντρί και ο λύκος να μείνει νηστικός;

δ) Με ποια αλγεβρική τιμή ταχύτητας φτάνει το κατσικάκι στο μαντρί;

ε) Να κάνετε σε βαθμολογημένα συστήματα αξόνων, τα διαγράμματα των αλγεβρικών τιμών επιτάχυνσης – χρόνου, θέσης – χρόνου και ταχύτητας – χρόνου για τα δυο ζώα.

Τα ζώα θεωρούνται υλικά σημεία.

Απάντηση 

Πολύ συχνά γινόμαστε μάρτυρες τροχαίων ατυχημάτων, που οφείλονται σε διάφορους λόγους. Ένα πολύ μεγάλο ποσοστό όμως οφείλεται στο ότι ο οδηγός δεν καταφέρνει να σταματήσει το αυτοκίνητό του, σε περίπτωση που συναντήσει κάποιο κίνδυνο. Φρενάρει μεν, αλλά δεν προλαβαίνει να σταματήσει είτε επειδή η απόσταση που τον χωρίζει από ένα εμπόδιο είναι πολύ μικρή είτε γιατί η ταχύτητά του είναι αρκετά μεγάλη. Ας μελετήσουμε λοιπόν αναλυτικότερα την απόσταση που θα διανύσει ένα αυτοκίνητο από τη στιγμή που αρχίζει να φρενάρει, μέχρι να σταματήσει.

Έστω λοιπόν ένα αυτοκίνητο που κινείται σε οριζόντιο δρόμο με ταχύτητα U_ο και σε μια στιγμή φρενάρει ώστε να μπλοκάρει του τροχούς και να μην στρέφονται.

Παίρνουμε τις δυνάμεις που ασκούνται στο αυτοκίνητο. Αυτές είναι το βάρος του, η κάθετη αντίδραση του επιπέδου και η τριβή ολίσθησης.

Διαβάστε τη συνέχεια

ή

Μήκος φρεναρίσματος και απόσταση ασφαλείας

 

 

Πάνω σε λείο οριζόντιο επίπεδο ηρεμεί το σύστημα των σωμάτων Σ1(σανίδα) και Σ2(κύβος) του σχήματος, με μάζες m₁ = 3kg και m₂ = 2kg αντίστοιχα, όπως φαίνεται στο σχήμα 1. Ασκούμε στο Σ1 οριζόντια δύναμη και μελετάμε τη συμπεριφορά του συστήματος.Α) Αν μεταξύ των σωμάτων δεν εμφανίζεται τριβή, τι κίνηση θα εκτελέσει κάθε σώμα;
Β) Αν μεταξύ των σωμάτων υπάρχει τριβή, με συντελεστές τριβής μ = μ_σ = 0,3 ποια είναι η μέγιστη τιμή της κοινής επιτάχυνσης των δύο σωμάτων ώστε να μην υπάρξει ολίσθηση του σώματος Σ2, πάνω στο Σ1; Ποια είναι η αντίστοιχη μέγιστη τιμή στο μέτρο F της ασκούμενης δύναμης;
Γ) Επαναλαμβάνουμε το πείραμα, με μέτρο δύναμης F = 18N.
α) Τι κίνηση θα εκτελέσει κάθε σώμα;
β) Ποια θα είναι τα μέτρα των επιταχύνσεων των σωμάτων;
γ) Να κάνετε στους ίδιους βαθμολογημένους άξονες, τις γραφικές παραστάσεις μετατόπισης – χρόνου για τα δύο σώματα από t₀ = 0, μέχρι t = 2s.
δ) Πόσο είναι το ελάχιστο μήκος της σανίδας Σ1, ώστε το σώμα Σ2 να παραμείνει πάνω της, μέχρι τη χρονική στιγμή t = 2s, αν η αρχική θέση του Σ2 είναι αυτή του σχήματος 1; Δίνεται η πλευρά του κύβου d = 0,5m.
Δίνεται g = 10m/s².

Απάντηση(Word)-Κατεβάστε το για σωστή εμφάνιση

Απάντηση (Pdf)

Η τροχαλία είναι μια απλή μηχανή, που μπορεί να βοηθήσει μια εργασία, με την αλλαγή διεύθυνσης ή της μείωσης του μέτρου της απαιτούμενης δύναμης. Χρησιμοποιώντας τη σταθερή (πάγια) τροχαλία Ρ1, την κινητή τροχαλία Ρ2 και δυο νήματα, πετυχαίνουμε αντίστοιχα τα παραπάνω. Το νήμα ν1 δένεται στο σώμα Α, περνάει από το αυλάκι της σταθερής τροχαλίας Ρ1, τυλίγεται γύρω από το αυλάκι της κινητής τροχαλίας Ρ2 και καταλήγει στον άξονα της σταθερής τροχαλίας Ρ1, σε ακλόνητο σημείο,  όπως φαίνεται στο παρακάτω σχήμα.
Το νήμα ν2 δένεται στο σώμα Σ και καταλήγει στον άξονα της κινητής τροχαλίας Ρ2.
Με αυτή τη διάταξη θέλουμε να σύρουμε το σώμα Σ, μάζας m_Σ = 400kg,  πάνω στο κεκλιμένο επίπεδο, γωνίας κλίσης  θ με ημθ = 0,6 και συνθ = 0,8. Το αντίβαρο Α που θα χρησιμοποιήσουμε έχει μάζα m_Α = 300kg, οι τροχαλίες είναι αμελητέας μάζας, δεν εμφανίζονται τριβές στους άξονές τους, τα νήματα αβαρή, μη εκτατά και δε γλιστράνε στα αυλάκια των τροχαλιών. Ο συντελεστής τριβής ολίσθησης μεταξύ του σώματος Σ και του κεκλιμένου επιπέδου είναι μ = 0,5 και η επιτάχυνση της βαρύτητας g = 10m/s².
i) Αν το αντίβαρο Α κατέλθει κατά Δx, το σώμα Σ μετατοπίζεται κατά
α) Δx                β) Δx/2             γ) 2Δx
Βρείτε και δικαιολογείστε τη σωστή απάντηση.
ii) Αν η επιτάχυνση με την οποία κατέρχεται το Α έχει μέτρο α, το σώμα Σ αποκτά επιτάχυνση μέτρου
α) α                  β) 2α                γ) α/2
Βρείτε και δικαιολογείστε τη σωστή απάντηση.
iii) Υπολογίστε το μέτρο της επιτάχυνσης κάθε σώματος.
iv) Ποιο είναι το μέτρο της τάσης κάθε νήματος;
v) Αν το σώμα Α απέχει αρχικά από το οριζόντιο έδαφος απόσταση h = 5m, ποιο θα είναι το μέτρο της ταχύτητας με την οποία θα χτυπήσει στο έδαφος;

Απάντηση(Word) (Κατεβάστε το για σωστή προβολή)

Απάντηση(Pdf)