Ίδια δύναμη, ίδια τελική ταχύτητα
του Διονύση Μάργαρη.
Κατηγορία: 1.2.1 Αναρτήσεις
Πάμε για ζύγιση στο Φεγγάρι
Ένα σώμα Σ, μάζας m = 120g, μπορεί να ζυγιστεί σε έναν τόπο, με δύο τρόπους. Χρησιμοποιώντας ένα δυναμόμετρο ώστε το σύστημα να ισορροπεί κατακόρυφο ή μια ζυγαριά με δίσκους και σταθμά, ώστε η φάλαγγα να είναι οριζόντια (βλέπετε και το σχήμα).
Α) Τι μετράμε με κάθε τρόπο;
Β) Οι δύο τρόποι ζύγισης θα δώσουν το ίδιο αποτέλεσμα για τη μάζα του σώματος;
Γ) Αν επαναλάβουμε τις δυο ζυγίσεις στην επιφάνεια της Σελήνης, όπου η επιτάχυνση της βαρύτητας είναι το 1/6 της γήινης, το αποτέλεσμα θα είναι:
α) 120g, 120g β) 20g, 120g γ) 20g, 20g
Ισορροπία πάνω σε ένα επιταχυνόμενο βαγόνι
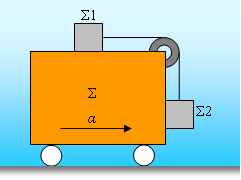Στο βαγόνι Σ του σχήματος, έχουμε προσαρμόσει ένα σύστημα δυο σωμάτων Σ1 και Σ2, με ίσες μάζες m1 = m2 = m, που συνδέονται με αβαρές μη εκτατό νήμα μέσω τροχαλίας. Ο συντελεστής στατικής τριβής είναι μ, ίδιος και για τα δυο σώματα με τις αντίστοιχες επιφάνειες που ακουμπούν και η επιτάχυνση της βαρύτητας είναι g. Η ελάχιστη τιμή του μέτρου της επιτάχυνσης για την οποία το σύστημα των δυο σωμάτων δεν κινείται ως προς το βαγόνι είναι
Το τούβλο γλίστρησε και έπεσε
Ένα αμαξίδιο, μάζας m1 = 3kg και μήκους l = 40cm, ηρεμεί πάνω σε ένα μακρύ οριζόντιο τραπέζι, στο οποίο μπορεί να κινείται χωρίς τριβές. Πάνω στην καρότσα του αμαξιδίου βρίσκεται ένα τούβλο μάζας m = 2kg, που αρχικά είναι ακίνητο. Κρεμάμε στην άκρη ενός αβαρούς νήματος ένα σώμα Σ μάζας m2 = 5kg, δένουμε την άλλη άκρη του νήματος στο αμαξίδιο, μέσω αβαρούς τροχαλίας, όπως στο σχήμα και αφήνουμε το σύστημα να κινηθεί από την ηρεμία. Πως θα απαντούσε (αν μπορούσε), ένα ακίνητο …ποντικάκι πάνω στο τραπέζι, στα παρακάτω θέματα;α) Αν το τούβλο δεν παρουσιάζει τριβή με την οριζόντια επιφάνεια του αμαξιδίου, τι θα του συμβεί όταν το αμαξίδιο κινηθεί; Ποια θα είναι η επιτάχυνση ααμ του αμαξιδίου;
β) Αν το τούβλο παρουσιάζει με την οριζόντια επιφάνεια του αμαξιδίου συντελεστή τριβής μ, πέφτει από το αμαξίδιο μετά από χρόνο t = 0,8s.
i) Βρείτε την επιτάχυνση α του αμαξιδίου.
ii) Υπολογίστε το συντελεστή τριβής μ.
Δίνεται ότι το νήμα που συνδέει το σώμα Σ με την τροχαλία είναι συνεχώς κατακόρυφο και g = 10m/s2.
Τριβή – Γενικές Ασκήσεις
Πατήστε την εικόνα
Πηγή: Ylikonet.gr
Κατακόρυφες βολές από ταράτσα (Α. Παπάζογλου)
Διαβάστε ΕΔΩ
Επίθεση στο κάστρο
Στη μάχη για την κατάκτηση ενός κάστρου ένας λεγεωνάριος, όταν βρέθηκε στη βάση του τείχους, ύψους H = 4m, ρίχνει πέτρα, κατακόρυφα προς τα πάνω, με αρχική ταχύτητα μέτρου υ0 = 8m/s, από σημείο Α σε υψόμετρο h = 1m πάνω από το έδαφος.
α) Θα φτάσει η πέτρα στο σημείο Β, που βρίσκεται στην ίδια κατακόρυφο με το Α και αντιστοιχεί στην κορυφή του τείχους;
β) Αν ναι ποια θα είναι η ταχύτητα της πέτρας στο σημείο Β;
γ) Ποιο είναι το μέγιστο ύψος από το έδαφος που θα φτάσει η πέτρα;
δ) Αν η πέτρα επιστρέψει στο σημείο βολής Α, τι ταχύτητα θα έχει;
ε) Ένας χωρικός, υπερασπιστής του τείχους, εκτοξεύει από το σημείο Β, προς τα κάτω με αρχική ταχύτητα ίδιου μέτρου υ0 = 8m/s δεύτερη πέτρα, η οποία κινείται ανάμεσα στα ίδια σημεία με την πρώτη. Ποια θα είναι η ταχύτητά της όταν φτάνει στο σημείο Α;
ε) Αν οι δύο σφαίρες εκτοξευτούν ταυτόχρονα, σε ποιο ύψος από το έδαφος θα μπορούσαν να συναντηθούν;
στ) Να γίνουν τα διαγράμματα θέσης –χρόνου σε κοινούς άξονες για τις δύο πέτρες.
Δίνεται g = 10m/s2 και η αντίσταση του αέρα αμελητέα.
Δυνάμεις και ισορροπίες (Δ. Μάργαρη)
Πάνω σε μια ζυγαριά ακριβείας, τοποθετούμε ένα μαγνήτη Μ, με αποτέλεσμα η ζυγαριά να δείχνει ένδειξη 5Ν. Στο άκρο του δυναμομέτρου του διπλανού σχήματος, το οποίο κρατάμε με το χέρι μας, αναρτούμε ένα σιδερένιο λουκέτο βάρους 2,5Ν.
- i) Αφού σχεδιάσετε τις δυνάμεις που ασκούνται στο μαγνήτη και στο λουκέτο, να υπολογίσετε τα μέτρα τους.
- ii) Μετακινούμε το δυναμόμετρο φέρνοντάς το σε θέση πάνω από το μαγνήτη, όπως στο δεύτερο σχήμα. Στη θέση αυτή ο μαγνήτης έλκει το λουκέτο ασκώντας του δύναμη 1Ν. Ποιες είναι τώρα οι ενδείξεις της ζυγαριάς και του δυναμομέτρου;
Προσοχή μην πέσεις από το κρεβάτι
Ένας τραυματισμός στο κεφάλι, όπως για παράδειγμα η διάσειση, μπορεί να προκληθεί από μεγάλη επιτάχυνση. Υποθέστε ότι ένα παιδί κυλάει έξω από το κρεβάτι του σε ύψος 0,4m από το πάτωμα. Αν το πάτωμα είναι ξύλινο το κεφάλι χρειάζεται διαδρομή 2mm για να σταματήσει, μετά την πρόσκρουση. Αν υπάρχει χαλί το αντίστοιχο διάστημα γίνεται 1cm.
α) Βρείτε το χρόνο που χρειάζεται και την ταχύτητα με την οποία χτυπάει στο πάτωμα.
β) Υπολογίστε το χρονικό διάστημα και την επιτάχυνση σε κάθε μια περίπτωση, προκειμένου να σταματήσει.
γ) Αν γνωρίζετε ότι επιτάχυνση μικρότερη από 800m/s2 για οποιοδήποτε χρονική διάρκεια, δε μπορεί να προκαλέσει τραυματισμό, ενώ επιτάχυνση πάνω από 1000m/s2, που διαρκεί τουλάχιστον 1ms, μπορεί να προκαλέσει διάσειση, εκτιμήστε τον κίνδυνο.
Δεχόμαστε ότι το σώμα παραμένει οριζόντιο κατά την πτώση και g = 10m/s2.
Παιδί σε αυτοκίνητο
Μέσα σε αυτοκίνητο που κινείται στην πόλη, με ταχύτητα υ0 = 64,8km/h, στη θέση του συνοδηγού η Άννα, φορώντας ζώνη ασφαλείας, κρατάει ευτυχισμένη το κοριτσάκι της μάζας m = 10kg, γιατί έτσι νομίζει ότι το προστατεύει…Δεν υπολόγισε όμως τον αφηρημένο οδηγό, που βγήκε, παραβιάζοντας το stop, κάθετα στην πορεία του αυτοκινήτου της οικογένειας. Χρειάστηκαν μόνο Δx = 2,7m για να ακινητοποιηθεί το αυτοκίνητο. Η Άννα μπορούσε (γιατί πήγαινε και Γυμναστήριο) να ασκεί με τα χέρια της δυνάμεις μέχρι 150Ν και ήταν η μόνη που μπορούσε να ασκήσει την απαιτούμενη δύναμη για την επιβράδυνση του παιδιού…
α) Ποιο ήταν το μέτρο της επιτάχυνσης του αυτοκινήτου; Συγκρίνετε αυτή την επιτάχυνση με την επιτάχυνση της βαρύτητας g = 10m/s2
β) Ποια δύναμη έπρεπε να ασκήσει η Άννα ώστε να συγκρατήσει το παιδί;
γ) Τι συμπεραίνετε ότι συνέβη στο παιδί;
