Η τροχαλία είναι μια απλή μηχανή, που μπορεί να βοηθήσει μια εργασία, με την αλλαγή διεύθυνσης ή της μείωσης του μέτρου της απαιτούμενης δύναμης. Χρησιμοποιώντας τη σταθερή (πάγια) τροχαλία Ρ1, την κινητή τροχαλία Ρ2 και δυο νήματα, πετυχαίνουμε αντίστοιχα τα παραπάνω. Το νήμα ν1 δένεται στο σώμα Α, περνάει από το αυλάκι της σταθερής τροχαλίας Ρ1, τυλίγεται γύρω από το αυλάκι της κινητής τροχαλίας Ρ2 και καταλήγει στον άξονα της σταθερής τροχαλίας Ρ1, σε ακλόνητο σημείο, όπως φαίνεται στο παρακάτω σχήμα.
Το νήμα ν2 δένεται στο σώμα Σ και καταλήγει στον άξονα της κινητής τροχαλίας Ρ2.
Με αυτή τη διάταξη θέλουμε να σύρουμε το σώμα Σ, μάζας mΣ = 400kg, πάνω στο κεκλιμένο επίπεδο, γωνίας κλίσης θ με ημθ = 0,6 και συνθ = 0,8. Το αντίβαρο Α που θα χρησιμοποιήσουμε έχει μάζα mΑ = 300kg, οι τροχαλίες είναι αμελητέας μάζας, δεν εμφανίζονται τριβές στους άξονές τους, τα νήματα αβαρή, μη εκτατά και δε γλιστράνε στα αυλάκια των τροχαλιών. Ο συντελεστής τριβής ολίσθησης μεταξύ του σώματος Σ και του κεκλιμένου επιπέδου είναι μ = 0,5 και η επιτάχυνση της βαρύτητας g = 10m/s2.
i) Αν το αντίβαρο Α κατέλθει κατά Δx, το σώμα Σ μετατοπίζεται κατά
α) Δx β) Δx/2 γ) 2Δx
Βρείτε και δικαιολογείστε τη σωστή απάντηση.
ii) Αν η επιτάχυνση με την οποία κατέρχεται το Α έχει μέτρο α, το σώμα Σ αποκτά επιτάχυνση μέτρου
α) α β) 2α γ) α/2
Βρείτε και δικαιολογείστε τη σωστή απάντηση.
iii) Υπολογίστε το μέτρο της επιτάχυνσης κάθε σώματος.
iv) Ποιο είναι το μέτρο της τάσης κάθε νήματος;
v) Αν το σώμα Α απέχει αρχικά από το οριζόντιο έδαφος απόσταση h = 5m, ποιο θα είναι το μέτρο της ταχύτητας με την οποία θα χτυπήσει στο έδαφος;
Απάντηση(Word) (Κατεβάστε το για σωστή προβολή)
Απάντηση(Pdf)






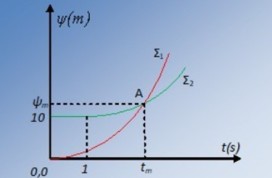 Το διάγραμμα θέσης – χρόνου αναφέρεται σε δύο μικρές σφαίρες Σ1 και Σ2, με μάζες m1 και m2 > m1, που βρίσκονται στο ίδιο κατακόρυφο επίπεδο και αφήνονται να εκτελέσουν ελεύθερη πτώση, απουσία αέρα, παράλληλα σε έναν κατακόρυφο άξονα Ψ΄Ψ, με θετική φορά προς τα κάτω. Η επιτάχυνση της βαρύτητας έχει μέτρο g = 10m/s2.
Το διάγραμμα θέσης – χρόνου αναφέρεται σε δύο μικρές σφαίρες Σ1 και Σ2, με μάζες m1 και m2 > m1, που βρίσκονται στο ίδιο κατακόρυφο επίπεδο και αφήνονται να εκτελέσουν ελεύθερη πτώση, απουσία αέρα, παράλληλα σε έναν κατακόρυφο άξονα Ψ΄Ψ, με θετική φορά προς τα κάτω. Η επιτάχυνση της βαρύτητας έχει μέτρο g = 10m/s2.