Κατηγορία: 1.1.1 Αναρτήσεις

του Αποστόλη Παπάζογλου

Για να διαβάσετε την άσκηση πατείστε

ΕΔΩ(Pdf)

του Διονύση Μάργαρη

Στον ίδιο ευθύγραμμο δρόμο, κινούνται δύο αυτοκίνητα Α και Β. Παίρνοντας κάποια  στιγμή σαν αρχή μέτρησης του χρόνου (t₀=0), ένας φίλος σας, μέτρησε τις ταχύτητες των δύο αυτοκινήτων και σχεδίασε σε κοινό διάγραμμα, τον τρόπο μεταβολής τους.

 

Συνέχεια

Στις κατοικημένες περιοχές το όριο ταχύτητας των αυτοκινήτων είναι υ_α = 60km/h. Ένα αυτοκίνητο έχει μέσο μήκος x = 3,5m και μέσο πλάτος ψ = 2m. Προκειμένου να διασχίσει κάθετα ένας πεζός το δρόμο, πρέπει να διανύσει απόσταση μεγαλύτερη από το πλάτος του αυτοκινήτου, πριν το αυτοκίνητο τον φτάσει. Για ασφάλεια πρέπει η απόσταση αυτή να είναι τουλάχιστον διπλάσια από το πλάτος του αυτοκινήτου. Η ταχύτητα βαδίσματος είναι υ_β = 4km/h.

α) Πόσο χρόνο χρειάζεται ο πεζός για να διανύσει απόσταση ίση με το πλάτος του αυτοκινήτου;
β) Πόσο διάστημα διανύει το αυτοκίνητο στον παραπάνω χρόνο; Γιατί η απάντηση αυτή είναι τόσο σημαντική;

γ) Αν ο πεζός δει το αυτοκίνητο σε απόσταση 28m, είναι ασφαλές να διασχίσει το δρόμο;

δ) Πόσο μακριά πρέπει να είναι το αυτοκίνητο από τον πεζό, ώστε να διασχίσει το δρόμο με ασφάλεια; Σε πόσα μήκη αυτοκινήτου αντιστοιχεί αυτή η απόσταση;

Απάντηση

Σε μια προσπάθεια κατάρριψης του παγκόσμιου ρεκόρ στο δρόμο των 800m, τον οποίο θα θεωρήσουμε ευθύγραμμο…, ένας αθλητής υπολόγισε να κάνει αυτή την απόσταση σε χρονική διάρκεια 1min 45s, τρέχοντας με σταθερή ταχύτητα. Μέχρι ένα σημείο της διαδρομής κατόρθωσε να διατηρήσει την ταχύτητα που είχε υπολογίσει, αλλά μετά από αυτό το σημείο συνέχισε με κίνηση ομαλά επιβραδυνόμενη, τέτοια που, όταν έκοβε το νήμα να έχει ταχύτητα μηδέν. Με αυτόν τον τρόπο τερμάτισε σε 1min 50s.

α) Να κάνετε ποιοτικά το διάγραμμα ταχύτητας – χρόνου για τον αθλητή.

β) Από το διάγραμμα να βρείτε ποια χρονική στιγμή άρχισε να επιβραδύνεται ο αθλητής και ποια είναι η αντίστοιχη επιβράδυνση.
γ) Tι ταχύτητα έχει ο αθλητής 10,5m πριν από τον τερματισμό;

 

 

 

 

ΑΠΑΝΤΗΣΗ

 

 

 

 

ΑΠΑΝΤΗΣΗ

Ένας ποδηλάτης αφήνει ένα σημείο Α μιας πόλης Π_Α στις 11.00 h (σύμφωνα με το ρολόι στο χέρι του) και κατευθύνεται προς σημείο Β μιας πόλης Π_Β με σταθερή ταχύτητα μέτρου υ_Α = 40 km/h. Στις 12.00 h ξεκινά από την ίδια πόλη ένα φορτηγάκι που κατευθύνεται και αυτό προς το σημείο Β με σταθερή ταχύτητα μέτρου υ_Β = 80 km/h. Τη στιγμή της συνάντησης ο ποδηλάτης πηδάει στο φορτηγάκι χωρίς αυτό να αλλάξει ταχύτητα και έτσι φτάνει στον προορισμό του 1,5h νωρίτερα.

α) Να γράψετε τις εξισώσεις κίνησης των δυο κινητών μέχρι τη στιγμή της συνάντησης.

β) Να προσδιορίσετε τη χρονική στιγμή και τη θέση της συνάντησης.

γ) Να βρείτε πόση είναι η απόσταση των δύο πόλεων.

δ) Να κάνετε τη γραφική παράσταση θέσης – χρόνου (χ→t) για τον ποδηλάτη.

ΑΠΑΝΤΗΣΗ

Αναδημοσιεύω από το site του Βαγγέλη Μαρούση https://vmarousis.blogspot.com

 

 

 

 

6 βασικές λυμένες ασκήσεις στην Ευθύγραμμη Ομαλή Κίνηση

 

Ένα αυτοκίνητο που κινείται σε άξονα έχει ταχύτητα υ₀ = 15 m/s και τη στιγμή t₀ = 0 περνάει από τη θέση χ₀ = 0. Με την ταχύτητα υ₀ κινείται για 5 s και στη συνέχεια κινείται με επιτάχυνση -3 m/s² για το χρονικό διάστημα 5 s – 15 s. Για το χρονικό διάστημα 15 s – 25 s επιταχύνεται με επιτάχυνση 1,5 m/s².

α) Να γίνει το διάγραμμα α→t

β) Να βρείτε τη θέση του αυτοκινήτου και την ταχύτητα στο τέλος κάθε φάσης της κίνησης.

γ) Ποιο είναι το συνολικό διάστημα που διανύει το αυτοκίνητο;

δ) Να γίνουν τα διαγράμματα χ→t και υ →t.

 

Απάντηση

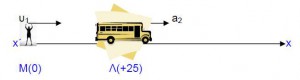Ένας μαθητής τρέχει με σταθερή ταχύτητα 6 m/s, προς τη στάση λεωφορείων. Τη στιγμή που απέχει 25 m από τη στάση, βλέπει το λεωφορείο να ξεκινάει με επιτάχυνση 1 m/s² .

α) Να αποδείξετε ότι ο μαθητής δεν προλαβαίνει το λεωφορείο.

β) Ποια η ελάχιστη απόσταση στην οποία θα βρεθεί με το λεωφορείο και ποια η αντίστοιχη χρονική στιγμή;

γ) Ποια σταθερή ταχύτητα έπρεπε να είχε ο μαθητής, ώστε να προλάβαινε το λεωφορείο;

δ) Μπορείτε να κάνετε τα διαγράμματα x = f(t) στο ίδιο σύστημα αξόνων, στην περίπτωση που δεν προλαβαίνει το λεωφορείο;

Η συνέχεια και η απάντηση ΕΔΩ