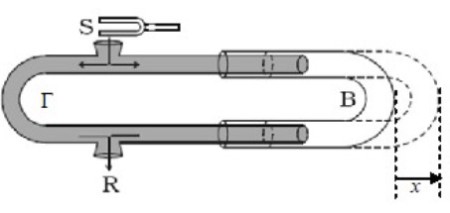
Ένα διάμηκες ηχητικό κύμα συχνότητας f = 425Hz, δημιουργείται από το διαπασών S και εισέρχεται στο σωλήνα του σχήματος (σωλήνας Quincke). Το τμήμα Γ είναι σταθερού μήκους ενώ το τμήμα Β είναι κινητό και μπορούμε να αυξομειώνουμε το μήκος του. Αρχικά το τμήμα Β είναι τέρμα αριστερά δηλαδή απόσταση x = 0. Ο ήχος διασπάται σε δύο ηχητικά κύματα πλάτους ίδιου πλάτους Α, που ακολουθούν τις διαδρομές SBR και SΓR, για τις οποίες γνωρίζουμε την αρχική διαφορά SBR – SΓR = s2 – s1 = 0,8m. Στη συνέχεια τα δυο κύματα συμβάλλουν στο σημείο του σωλήνα, λίγο πριν την έξοδο στο δέκτη R. Η ταχύτητα του ήχου στον αέρα είναι υηχ = 340m/s και θεωρούμε αμελητέα τη μεταβολή του πλάτους των δύο κυμάτων, μέχρι τη στιγμή της συμβολής.
i) Ο δέκτης λαμβάνει μέγιστο ή ελάχιστο πλάτος ως αποτέλεσμα της συμβολής;
ii) Διερευνείστε το πλάτος του ήχου που θα λάβει ο δέκτης R, αν από την αρχική του θέση ο κινητός σωλήνας εξέλθει επιπλέον κατά
α) x = 0,1m
β) x = 0,2m
γ) x = 0,4m
iii) Μπορείτε να βρείτε μια χρησιμότητα αυτού του σωλήνα;
iv) Τα δυο ηχητικά κύματα που φτάνουν στο δέκτη, μπορούν πραγματικά να έχουν το ίδιο πλάτος;
v) Για καθηγητές
Αν η ένταση του ήχου όταν ανιχνεύουμε μέγιστο είναι I1 = 0,09W/m2 και όταν ανιχνεύουμε ελάχιστο I2 = 0,01W/m2 ποιος είναι ο λόγος των πλατών, που φτάνουν στον ανιχνευτή;
Μήνας: Δεκέμβριος 2022
Από ένα διάγραμμα συμβολής κυμάτων
Τη χρονική στιγμή t = 0, ξεκινούν από δυο σύγχρονες πηγές Π1, Π2 να παράγονται αρμονικά κύματα πλάτους A = 0,1m, που διαδίδονται στην επιφάνεια υγρού με ταχύτητα υδ = 2m/s. Οι πηγές βρίσκονται στα σημεία Κ και Λ του υγρού με ΚΛ = d = 4,4m.
Στο παρακάτω διάγραμμα φαίνεται η γραφική παράσταση της απομάκρυνσης για ένα σημείο Σ του υγρού, που οι αποστάσεις του από τις πηγές είναι r1 και r2 > r1.
- Εξηγείστε το είδος της συμβολής που συμβαίνει στο σημείο Σ και να κάνετε τη γραφική παράσταση του πλάτους της ταλάντωσης του Σ σε συνάρτηση με το χρόνο.
- Υπολογίστε τις αποστάσεις r1, r2 και βρείτε σε ποιον κροσσό συμβολής, ως προς τη μεσοκάθετο του ΚΛ, βρίσκεται το σημείο Σ.
- Η υπερβολή που διέρχεται από το σημείο Σ, τέμνει το ευθύγραμμο τμήμα ΚΛ σε σημείο Β. Βρείτε πόσα σημεία αποσβεστικής συμβολής βρίσκονται στο ευθύγραμμο τμήμα ΚΒ, μετά τη συμβολή των κυμάτων.
- Μειώνουμε ταυτόχρονα την περίοδο ταλάντωσης των πηγών, ώστε να παραμένουν σύγχρονες. Ποια είναι η ελάχιστη μείωση, που μπορούμε να κάνουμε ώστε το σημείο Σ να είναι σημείο αποσβεστικής συμβολής;