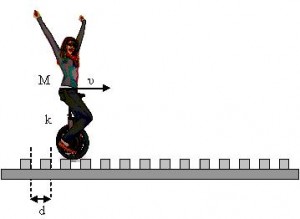Στην κινητή γέφυρα που ενώνει τη Λευκάδα με τη στεριά, προκειμένου να εμποδίζονται τα οχήματα να κινούνται με μεγάλες ταχύτητες έχουν τοποθετηθεί εγκάρσια μεταλλικές ράβδοι σχήματος ορθογωνίου, όπως φαίνονται στην διατομή του σχήματος, που ανά δύο απέχουν μεταξύ τους απόσταση d, όπως στο σχήμα.
Μήνας: Ιούλιος 2015
Σύνθεση εξισώσεων α.α.τ. με Geogebra
Του Φώτη Ζαφειριάδη
Πατείστε στην παρακάτω εικόνα
Φθίνουσα ταλάντωση με όχι τόσο …μικρή απόσβεση
Σώμα μάζας m = 5kg εκτελεί ευθύγραμμη κίνηση σε άξονα xx΄με την επίδραση δύο δυνάμεων. Μιας δύναμης επαναφοράς με αλγεβρική τιμή Fεπ = -40x (S.I.) και μιας δύναμης απόσβεσης με αλγεβρική τιμή Fαπ = -20υ (S.I.), όπου x και υ οι αλγεβρικές τιμές θέσης και ταχύτητας αντίστοιχα. Το σώμα εκτελεί φθίνουσα ταλάντωση και οι χρονικές εξισώσεις της απομάκρυνσης και της ταχύτητας είναι
Μερικές «αντιφάσεις» στην ελαστική κρούση
Του Διονύση Μάργαρη
Κατά την μετωπική ελαστική κρούση έχουμε καταλήξει στις σχέσεις:
Για τις ταχύτητες των δύο υλικών σημείων που συγκρούονται ελαστικά και που το δεύτερο σώμα είναι αρχικά ακίνητο.
Οι τελικές ταχύτητες συνεπώς των δύο σωμάτων, εξαρτώνται καθαρά από τις σχέσεις των μαζών τους.
Αλλά τότε ανάλογα με την σχέση των δύο μαζών, θα έχουμε διαφορετικά «πρακτικά» αποτελέσματα και μερικά από αυτά μπορούν να δημιουργούν «εκπλήξεις»!
Ας ξεκινήσουμε από μια πολύ συχνή περίπτωση:
Χάσιμο επαφής και απλή αρμονική ταλάντωση
Βασισμένο στην αντίστοιχη εργασία του Σταύρου Πρωτογεράκη.
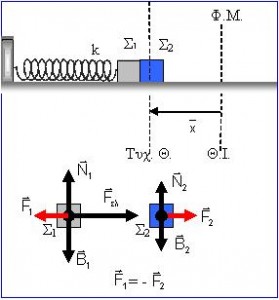
Α) Έστω σύστημα δύο σωμάτων Σ1 και Σ2, με μάζες m1 και m2, που βρίσκονται σε επαφή πάνω σε οριζόντιο επίπεδο. Το Σ1 είναι δεμένο στο άκρο οριζόντιου ελατηρίου (όπως στο σχήμα) σταθεράς k ενώ το Σ2 δεν είναι κολλημένο με το Σ1. Μετακινούμε το σύστημα συμπιέζοντας το ελατήριο και το αφήνουμε ελεύθερο, οπότε εκτελεί α.α.τ.
Αλλάζοντας την ενέργεια της α.α.τ.
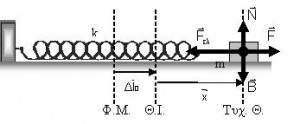
Σώμα μάζας m ηρεμεί πάνω σε λείο κεκλιμένο επίπεδο γωνίας κλίσης φ, όπου ημφ= 0,5 με τη βοήθεια ιδανικού ελατηρίου σταθεράς k, που έχει το πάνω άκρο του ακλόνητο, όπως φαίνεται στο σχήμα. Εκτρέπουμε το σώμα φέρνοντάς το στη θέση φυσικού μήκους του ελατηρίου και το αφήνουμε ελεύθερο να εκτελέσει α.α.τ. Κάποια στιγμή που το σώμα βρίσκεται σε ακραία θέση το σταματάμε. Στη συνέχεια μεγαλώνουμε τη γωνία κλίσης σε θ ώστε ημθ = 0,6 και αφήνουμε το σώμα ελεύθερο να συνεχίσει την ταλάντωσή του από τη θέση που το σταματήσαμε. Αν Ε η ενέργεια της αρχικής ταλάντωσης και Ε΄η ενέργεια της νέας ταλάντωσης
Δείξτε ότι το σώμα θα εκτελέσει α.α.τ.
Για να δείξουμε ότι ένα σώμα εκτελεί απλή αρμονική ταλάντωση (α.α.τ.), αρκεί
α) Να υπάρχει θέση ισορροπίας (Θ.Ι.), δηλαδή θέση όπου …
Ένα συντριβάνι από νερό και … λάδι
Μια δεξαμενή ανοικτή στην ατμόσφαιρα περιέχει δύο στρώματα διαφορετικών υγρών. Ένα στρώμα νερού ύψους h1 = 2 m και ένα στρώμα λαδιού ύψους h2 = 4 m. Η δεξαμενή φέρει, σε ύψος h3 = 1m από το οριζόντιο έδαφος, πλευρικό οριζόντιο σωλήνα με κατακόρυφο ακροφύσιο, η έξοδος του οποίου βρίσκεται στο ίδιο οριζόντιο επίπεδο με τη διαχωριστική επιφάνεια των δύο υγρών, όπως στο σχήμα, με τη στρόφιγγα αρχικά κλειστή. Η διάμετρος του οριζόντιου σωλήνα είναι 0,2 m και του άκρου Γ του ακροφυσίου 0,1 m. Αν ανοίξουμε τη στρόφιγγα:
(α) Υπολογίστε την αρχική ταχύτητα του νερού στο άκρο Γ του ακροφυσίου.
(β) Προσδιορίστε το αρχικό ύψος h του πίδακα.
(γ) Υπολογίστε την πίεση στον οριζόντιο σωλήνα.
Δίνονται ρν= 1000 kg/m3, ρλ= 700 kg/m3, g = 10 m/s2, η διάμετρος της δεξαμενής πολύ μεγαλύτερη από αυτές των σωλήνων, τα υγρά θεωρούνται ιδανικά.
