Σε μια ταινία Γουέστερν τρεις ληστές Α, Β και Γ συνεργάζονται για να κλέψουν μια άμαξα με χρυσό, συνολικής μάζας M = 350kg (σχήμα 1). Ο Α λύνει τα άλογα και η άμαξα ξεκινώντας από την ηρεμία κατεβαίνει τον κεκλιμένο δρόμο του σχήματος, γωνίας κλίσης θ = 120 και μήκους s = 25m. Στη συνέχεια μπαίνει σε οριζόντιο δρόμο, αλλά το πρόβλημα είναι ότι στο τέλος του υπάρχει γκρεμός. Οι ληστές Β και Γ με μάζες mB = 85kg και mΓ = 65kg αντίστοιχα, περιμένουν πάνω στα κλαδιά ενός δέντρου, σε ύψος h = 1,8m από την άμαξα και σε απόσταση d = 40m από το χείλος του γκρεμού, έτοιμοι να πέσουν μαζί κατακόρυφα, καθώς η άμαξα θα περάσει κάτω από το δέντρο. Η άμαξα κινείται χωρίς τριβές και αντιστάσεις, όλα τα σώματα θεωρούνται ως υλικά σημεία και g = 10m/s2.
α) Με ποιο μέτρο ταχύτητας φτάνει η άμαξα στο δέντρο;
β) Αν χρειάζονται Δt = 5s για να αρπάξουν το χρυσό και να πηδήξουν έξω από την άμαξα, θα το καταφέρουν πριν αυτή πέσει στο γκρεμό;
γ) Όταν οι δύο ληστές πηδήξουν στην άμαξα, διατηρείται η κινητική ενέργεια του συστήματος; Αν όχι αυξάνεται ή μειώνεται και πόσο;
δ) Αφού υπολογίσετε το μέτρο της ορμής του συστήματος αμέσως πριν και αμέσως μετά την επιβίβαση των ληστών στην άμαξα, να εξετάσετε αν η ορμή του συστήματος διατηρείται. Αν δεν διατηρείται, μπορείτε να εξηγήσετε ποια δύναμη ευθύνεται;
Δίνονται g = 10m/s2, ημ120 = 0,2
Κατηγορία: 3.021 Διατήρηση της ορμής- Αναρτήσεις
Ο ρόλος του τοίχου

Ζητήσαμε από τον κυρ Βασίλη τον ξυλουργό, να σκάψει σε ένα κυβικό κομμάτι ξύλου, ένα αυλάκι ημικυλινδρικού σχήματος κέντρου Ο και ακτίνας R = 0,8m, την κατακόρυφη τομή του οποίου βλέπουμε στο σχήμα 1. Δημιουργήθηκε έτσι το σώμα Σ1 μάζας m1. Στη συνέχεια το λούστραρε μέχρι να γίνει εντελώς λείο, ώστε να το χρησιμοποιήσουμε σε ένα πείραμα.
Τοποθετούμε το σώμα Σ1 κολλητά σε κατακόρυφο τοίχο και πάνω σε λείο οριζόντιο δάπεδο. Από το ανώτερο σημείο του Α αφήνουμε ελεύθερο να ολισθήσει ένα δεύτερο σώμα Σ2 μάζας m2 αμελητέων διαστάσεων, με m1 = 3m2. Τριβές αμελητέες και η βαρυτική επιτάχυνση g = 10m/s2.
α) Το σώμα Σ1 θα κινηθεί; Δικαιολογείστε την απάντησή σας.
β) Ποια είναι η μέγιστη τιμή που αποκτά το μέτρο της ταχύτητας του Σ2;
γ) Υπολογίστε το μέγιστο ύψος που θα φτάσει το σώμα Σ2 , μετρημένο από το κατώτερο σημείο Β του ημικυλίνδριου καθώς και τη γωνία φ, που σχηματίζει τότε η επιβατική ακτίνα με την κατακόρυφη.
δ) Καθ’ όλη τη διάρκεια του φαινομένου, τι συμβαίνει με το μέτρο της κάθετης αντίδρασης του δαπέδου, πάνω στο Σ1; Μεταβάλλεται ή μένει σταθερό; Δικαιολογείστε την απάντησή σας.
Μετά την εκτόξευση πως θα σταματήσει;
 Μια ομάδα μαθητών, θέλοντας να μελετήσει την αρχή διατήρησης ορμής κατά τη διάσπαση ενός συστήματος σωμάτων, έφτιαξε τη διάταξη του σχήματος, που μοιάζει με πύραυλο και αποτελείται από τρία σώματα, σε επαφή μεταξύ τους, που ηρεμούν πάνω σε λείο οριζόντιο δάπεδο. Το μεσαίο σώμα Σ2 έχει μάζα Μ = 6Kg και τα ακραία Σ1 και Σ3 έχουν ίσες μάζες m = 2kg το καθένα. Μεταξύ των σωμάτων τοποθέτησαν ελάχιστη ποσότητα εκρηκτικού υλικού και φυτίλια κατάλληλου μήκους, τα οποία και άναψαν, ώστε να πυροδοτήσουν διαδοχικά τα εκρηκτικά σε καθορισμένες χρονικές στιγμές.
Μια ομάδα μαθητών, θέλοντας να μελετήσει την αρχή διατήρησης ορμής κατά τη διάσπαση ενός συστήματος σωμάτων, έφτιαξε τη διάταξη του σχήματος, που μοιάζει με πύραυλο και αποτελείται από τρία σώματα, σε επαφή μεταξύ τους, που ηρεμούν πάνω σε λείο οριζόντιο δάπεδο. Το μεσαίο σώμα Σ2 έχει μάζα Μ = 6Kg και τα ακραία Σ1 και Σ3 έχουν ίσες μάζες m = 2kg το καθένα. Μεταξύ των σωμάτων τοποθέτησαν ελάχιστη ποσότητα εκρηκτικού υλικού και φυτίλια κατάλληλου μήκους, τα οποία και άναψαν, ώστε να πυροδοτήσουν διαδοχικά τα εκρηκτικά σε καθορισμένες χρονικές στιγμές.
Τη χρονική στιγμή t0 = 0, το Σ1 εκτοξεύεται προς τα αριστερά, με ταχύτητα μέτρου |υ1| = 4m/s, ενώ τη χρονική στιγμή t1 =0,8s, το Σ3 εκτοξεύεται προς τα δεξιά, με ταχύτητα μέτρου |υ3| =5m/s. Οι ταχύτητες είναι μετρημένες από έναν ακίνητο παρατηρητή, οι εκρήξεις διαρκούν αμελητέο χρονικό διάστημα και η αντίσταση του αέρα θεωρείται αμελητέα.
α) Ποια είναι η ταχύτητα του τμήματος Σ2-Σ3, αμέσως μετά την εκτόξευση του Σ1;
β) Ποια είναι η ταχύτητα του Σ2 αμέσως μετά την εκτόξευση του Σ3;
γ) Ποιο είναι το συνολικό ποσό της ενέργειας που εκλύθηκε από τα εκρηκτικά, αν το 58,7% αυτής έγινε θερμότητα και ακτινοβολία;
δ) Ποια θα είναι η μετατόπιση κάθε σώματος τη χρονική στιγμή t2 = 2,8s;
ε) Ποια θα έπρεπε να είναι η ταχύτητα εκτόξευσης του Σ3 ώστε το Σ2 να ακινητοποιηθεί;
Ο Σούπερμαν σώζει τη Λόις
 Σε μια σκηνή του γνωστού κόμικ, ο Σούπερμαν μπαίνει μπροστά από την Λόις Λέιν, για να την σώσει από τις σφαίρες του Λεξ Λούθορ. Η καραμπίνα του Λεξ, περιέχει φυσίγγιο που ρίχνει N = 150 μικρά σφαιρίδια, μάζας m = 0,6g το καθένα και ταχύτητας μέτρου |υ1| = 600m/s. Τα σφαιρίδια χτυπούν ταυτόχρονα κάθετα στο στήθος του Σούπερμαν και ανακρούουν με ταχύτητα μέτρου |υ2| = 600m/s, αντίθετης φοράς από την αρχική.
Σε μια σκηνή του γνωστού κόμικ, ο Σούπερμαν μπαίνει μπροστά από την Λόις Λέιν, για να την σώσει από τις σφαίρες του Λεξ Λούθορ. Η καραμπίνα του Λεξ, περιέχει φυσίγγιο που ρίχνει N = 150 μικρά σφαιρίδια, μάζας m = 0,6g το καθένα και ταχύτητας μέτρου |υ1| = 600m/s. Τα σφαιρίδια χτυπούν ταυτόχρονα κάθετα στο στήθος του Σούπερμαν και ανακρούουν με ταχύτητα μέτρου |υ2| = 600m/s, αντίθετης φοράς από την αρχική.
Πηδώντας στο ασανσέρ πριν τη συντριβή
Ρίχνοντας και πιάνοντας την μπάλα.

Ένας αθλητής στέκεται πάνω σε μία ακίνητη πλατφόρμα που μπορεί να κινηθεί σε λεία επιφάνεια. O αθλητής ρίχνει μια μπάλα προς το ακλόνητο πέτασμα στο άκρο της πλατφόρμας, με οριζόντια ταχύτητα ως προς το έδαφος υ1=20m/s . Η κατακόρυφη κίνηση της μπάλας εξαιτίας του βάρους της, μπορεί να αγνοηθεί. Καθώς η μπάλα χτυπά στο πέτασμα ανακρούεται με ταχύτητα μέτρου υ1΄=20m/s και επιστρέφει. Η μάζα του συστήματος αθλητή – πλατφόρμας είναι Μ=80kg ενώ της μπάλας m=0,5kg.
1. Υποστηρίζεται ότι η πλατφόρμα μένει ακίνητη, μέχρι να κτυπήσει στο πέτασμα η μπάλα. Να εξηγήσετε αν αυτό είναι σωστό ή λανθασμένο.
2. Να υπολογίσετε την ταχύτητα του συστήματος αθλητή-πλατφόρμα, μετά την κρούση της μπάλας με το πέτασμα.
3. Εάν ο αθλητής πιάσει την μπάλα καθώς αυτή επιστρέφει προς το μέρος του, ποια θα είναι τελικά η ταχύτητα του συστήματος;
Μια άσκηση του Διονύση Μάργαρη.
Από κατακόρυφη σε οριζόντια βολή
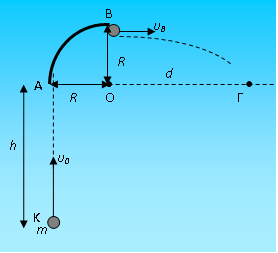 Το σημειακό αντικείμενο του σχήματος έχει μάζα m = 0,5kg και εκτοξεύεται κατακόρυφα προς τα πάνω από το σημείο Κ. Αφού ανέλθει κατά h = 2m, εισέρχεται εφαπτομενικά στο λείο ακλόνητο τεταρτοκύκλιο κέντρου Ο και ακτίνας R = 1m και ολισθαίνει από το Α ως το Β.Αφού εγκαταλείψει το τεταρτοκύκλιο στο σημείο Β, με οριζόντια ταχύτητα υΒ περνάει από το σημείο Γ, που βρίσκεται στο ίδιο οριζόντιο επίπεδο με τα σημεία Ο και Α, όπου ΟΓ = d = 3m.
Το σημειακό αντικείμενο του σχήματος έχει μάζα m = 0,5kg και εκτοξεύεται κατακόρυφα προς τα πάνω από το σημείο Κ. Αφού ανέλθει κατά h = 2m, εισέρχεται εφαπτομενικά στο λείο ακλόνητο τεταρτοκύκλιο κέντρου Ο και ακτίνας R = 1m και ολισθαίνει από το Α ως το Β.Αφού εγκαταλείψει το τεταρτοκύκλιο στο σημείο Β, με οριζόντια ταχύτητα υΒ περνάει από το σημείο Γ, που βρίσκεται στο ίδιο οριζόντιο επίπεδο με τα σημεία Ο και Α, όπου ΟΓ = d = 3m.
α) Ποια είναι η ταχύτητα υΒ του σώματος στο Β;
ΣΥΝΕΧΕΙΑ(pdf)



