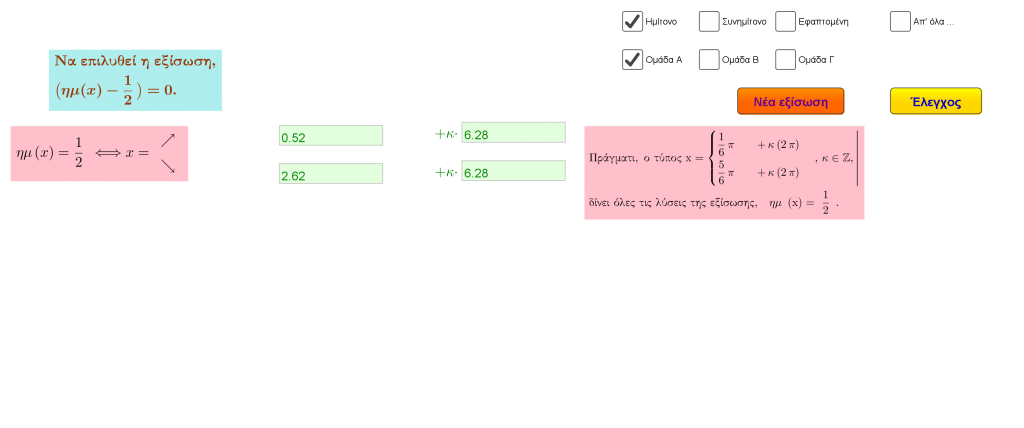
Στην ακόλουθη διαδραστική εφαρμογή, παριστάνεται γραφικά ο τριγωνομετρικός κύκλος και, με τη βοήθειά του, υπολογίζονται οι τριγωνομετρικοί αριθμοί γωνίας στο ![[0,2\pi]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-2b1273d522dc722fe2c9c22785016e14_l3.png?x32006 "Rendered by QuickLaTeX.com")
.
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Γεωμετρία Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 09-03-2019
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 18-07-2018
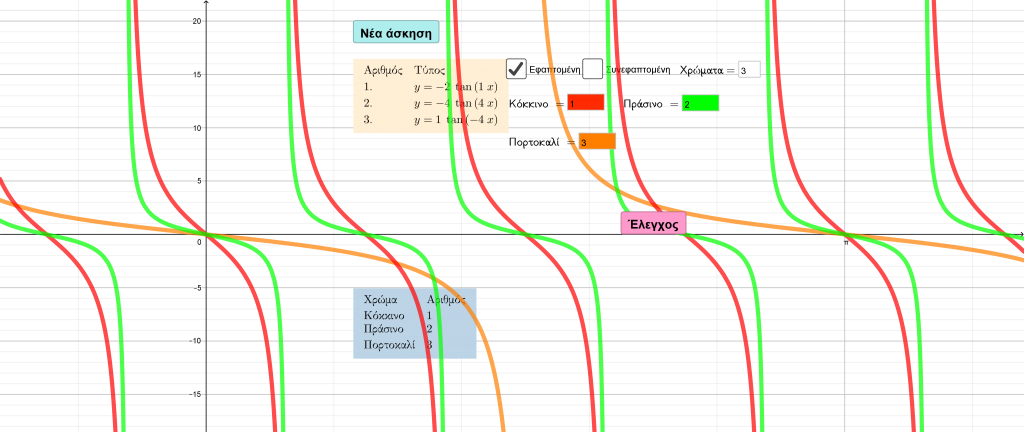
Αναγνωρίζετε την καμπύλη της εφαπτομένης και της συνεφαπτομένης;
Θα μπορούσατε να αντιστοιχίσετε διάφορα γραφήματα, τέτοιων συναρτήσεων, στους τύπους τους;
Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, ίσως να επαναλάβετε ορισμένα βασικά συμπεράσματα της θεωρίας, σχετικά με τη μορφή αυτών των γραφικών παραστάσεων, σε συνδυασμό με τις γνωστές συμμετρίες, που προκύπτουν, για γραφήματα συναρτήσεων όπου οι τύποι τους συνδέονται με βάση συγκεκριμένες διεργασίες.
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 18-07-2018
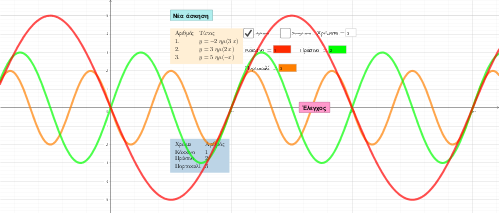
Αναγνωρίζετε τις καμπύλες των ημιτονοειδών και των συνημιτονοειδών συναρτήσεων;
Θα μπορούσατε να αντιστοιχίσετε διάφορα γραφήματα, τέτοιων συναρτήσεων, στους τύπους τους;
Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, ίσως να επαναλάβετε ορισμένα βασικά συμπεράσματα της θεωρίας, σχετικά με τη μορφή αυτών των γραφικών παραστάσεων, σε συνδυασμό με τις γνωστές συμμετρίες, που προκύπτουν, για γραφήματα συναρτήσεων όπου οι τύποι τους συνδέονται με βάση συγκεκριμένες διεργασίες.
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 01-01-2018
Η γενίκευση της έννοιας της γωνίας, όπως και των αντίστοιχων τριγωνομετρικών αριθμών της, αναδεικνύεται με τη βοήθεια του τριγωνομετρικού κύκλου. Ο τριγωνομετρικός κύκλος, ένας μοναδιαίος κύκλος με κέντρο την αρχή 
ενός ορθοκανονικού συστήματος συντεταγμένων 
, μπορεί να δεχθεί, ως επίκεντρη, μια οποιαδήποτε γωνία, 
, η οποία, μάλιστα, τοποθετείται έχοντας ως αρχική πλευρά της τον ημιάξονα 
. Αν συμβολίσουμε με 
το σημείο στο οποίο η τελική πλευρά τέμνει τον κύκλο, τότε,
![\[ \mathrm{cos}(\omega)=x,\,\, \mathrm{ sin}(\omega)=y,\,\, \mathrm{ tan}(\omega)=\frac{y}{x},\,\, \mathrm{ ctg}(\omega)=\frac{x}{y}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-819637aae64f79e18a4bc145d8b3e376_l3.png?x32006 "Rendered by QuickLaTeX.com")
Παρεμπιπτόντως, το πρόσημο της γωνίας καθορίζει τη φορά κίνησης της τελικής πλευράς, με το θετικό να αντιστοιχεί στην αριστερόστροφη, ωσότου επιτευχθεί το αντίστοιχο “άνοιγμα”.
Γνωστές σχέσεις μεταξύ γωνιών (αντίθετες γωνίες, παραπληρωματικές γωνίες, συμπληρωματικές γωνίες, γωνίες που διαφέρουν κατά 
, γωνίες που διαφέρουν κατά 
, κ.ά.) μπορούν να παρασταθούν στον τριγωνομετρικό κύκλο, ο οποίος προσφέρεται για τη διερεύνηση των αντίστοιχων σχέσεων μεταξύ των τριγωνομετρικών αριθμών αυτών των γωνιών και τελικά στην αναγωγή τους στο πρώτο τεταρτημόριο.
Τα προηγούμενα μπορούν να γίνουν περισσότερο κατανοητά μέσω της διαδραστικής εφαρμογής που ακολουθεί.
Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 27-12-2016
Μπορείτε να ανακαλύψετε, με τη βοήθεια της παρακάτω διαδραστικής εφαρμογής, το λόγο που τα τετράγωνα των πλευρών ενός τριγώνου έχουν “παραβατική” συμπεριφορά και το νόμο που μπορεί να τα ελέγξει;
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 04-03-2016
Με τη βοήθεια της παρακάτω διαδραστικής εφαρμογής, μπορείτε να εξασκηθείτε στη μελέτη ορισμένων βασικών μορφών τριγωνομετρικών συναρτήσεων.
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 14-02-2016
Με τη βοήθεια της παρακάτω διαδραστικής εφαρμογής, μπορείτε να εξασκηθείτε στην επίλυση ορισμένων βασικών μορφών τριγωνομετρικών εξισώσεων.
