Στο Γυμνάσιο, ένα από τα θέματα της Γεωμετρίας όπου σημαντική μερίδα μαθητών συναντά δυσκολίες, ειδικά στην Α΄ τάξη, είναι η χάραξη των υψών ενός τριγώνου.
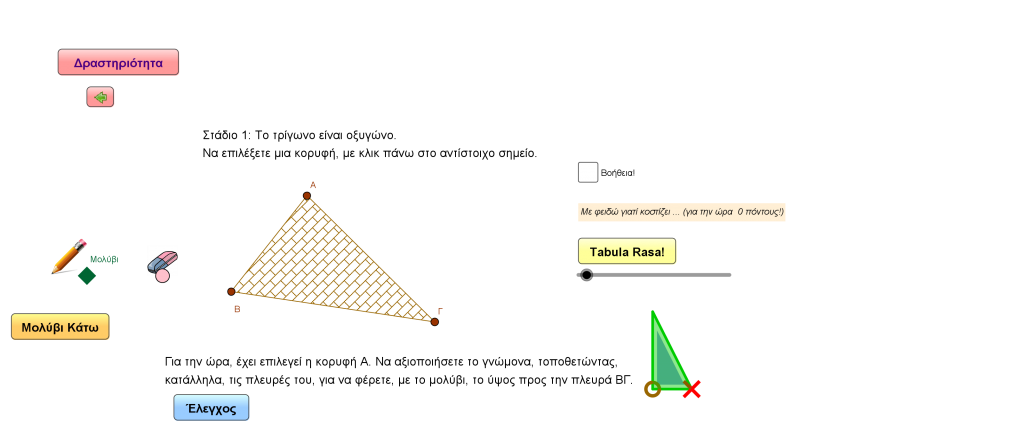
Η αδυναμία αρκετών μαθητών να σχεδιάσουν σωστά τα ύψη ενός τριγώνου γίνεται περισσότερο εμφανής στις περιπτώσεις του ορθογώνιου και αμβλυγώνιου τριγώνου. Οι πιο χαρακτηριστικές αστοχίες παρατηρούνται κατά την ορθή τοποθέτηση και σταθεροποίηση του γνώμονα, έτσι, ώστε να επιτευχθεί απόλυτη εφαρμογή με την πλευρά που βρίσκεται απέναντι από την κορυφή του τριγώνου από την οποία πρέπει να χαραχτεί το ύψος. Επίσης, η αποδοχή ότι το ύψος μπορεί να βρεθεί εκτός του τριγώνου, στην περίπτωση του αμβλυγώνιου τριγώνου, ή ότι συμπίπτει με κατάλληλη πλευρά του, όταν το τρίγωνο είναι ορθογώνιο, είναι ένα ζήτημα που απαιτεί ιδιαίτερη διδακτική προσέγγιση.
Στην παρακάτω εφαρμογή, μέσα από ένα πρόβλημα, γίνεται προσπάθεια οι μαθητές να ενεργοποιηθούν επιχειρώντας να βοηθήσουν έναν αρχιτέκτονα, ο οποίος προσπαθεί να σχεδιάσει τα κάθετα υποστυλώματα από τις κορυφές διάφορων τριγωνικών στεγών προς τις απέναντι πλευρές τους. Ουσιαστικά, πρόκειται για την κατασκευή των υψών ενός τριγώνου για διάφορα είδη τριγώνων. Η εμπλοκή των μαθητών με τα διαδραστικά χαρακτηριστικά που ενσωματώνει η εφαρμογή ίσως να ενθαρρύνει την ενασχόληση με το θέμα, παρέχοντάς τους κατάλληλα κίνητρα αλλά και βοήθειες για την ολοκλήρωση των ερωτημάτων που διαπραγματεύεται.
Εσείς, μπορείτε να βοηθήσετε ή μήπως ανήκετε στην κατηγορία των ανθρώπων που υποφέρουν από “υψο” … φοβία;