Όπως γνωρίζετε, κατά την παραγώγιση, μιας παραγωγίσιμης συνάρτησης, προκύπτει, μονοσήμαντα, μια νέα συνάρτηση, η παράγωγός της.
Η αντίστροφη διεργασία, για μια συνάρτηση η οποία έχει αρχική, οδηγεί, ουσιαστικά, σε μια διαδικασία επιλογής από ένα σύνολο συναρτήσεων.
(Οι συναρτήσεις αυτού του συνόλου έχουν, προφανώς, κοινό χαρακτηριστικό την ισότητα των παραγώγων τους.)
Το σύνολο όλων αυτών των αρχικών συναρτήσεων, για μια συνάρτηση, είναι το αόριστο ολοκλήρωμά της.
Ωστόσο, για λόγους απλότητας, σχεδόν, πάντοτε αποφεύγεται ο συμβολισμός των συνόλων χαλκεύοντας, έτσι, τον πραγματικό χαρακτήρα των ολοκληρωμάτων καθώς και τη φύση των επαγόμενων πράξεων. Τούτο οφείλεται στην “ταύτιση” του ολοκληρώματος, τροποντινά, μ’ έναν “αντιπρόσωπο” του συνόλου.
Έτσι, τα αόριστα ολοκληρώματα αντικαθίστανται από κατάλληλες συναρτήσεις, που τα αντιπροσωπεύουν, ενώ οι μεταξύ τους πράξεις εκτελούνται μέσω των αντιπροσώπων τους.
Ακολούθως, θα διεισδύσουμε στην πραγματική υπόσταση της έννοιας της αντιπαραγώγισης, αναλύοντας αρκετά απ’ τα ζητήματα που θίχτηκαν παραπάνω, αλλά, και εδώ, με περισσότερες τεχνικές λεπτομέρειες.
Θεωρούμε ένα διάστημα ![]() της πραγματικής ευθείας. Έστω, επίσης,
της πραγματικής ευθείας. Έστω, επίσης, ![]() το σύνολο όλων των παραγωγίσιμων συναρτήσεων στο
το σύνολο όλων των παραγωγίσιμων συναρτήσεων στο ![]() και
και ![]() το σύνολο όλων των συναρτήσεων για τις οποίες υπάρχει αρχική συνάρτηση στο Δ. Ορίζουμε μια σχέση
το σύνολο όλων των συναρτήσεων για τις οποίες υπάρχει αρχική συνάρτηση στο Δ. Ορίζουμε μια σχέση ![]() στο
στο ![]() ως εξής:
ως εξής:
Αν ![]() , τότε,
, τότε,
![]()
(Δηλαδή, δύο στοιχεία του ![]() συνδέονται με τη σχέση
συνδέονται με τη σχέση ![]() , αν και μόνο αν έχουν την ίδια παράγωγο.)
, αν και μόνο αν έχουν την ίδια παράγωγο.)
Η προηγούμενη σχέση είναι μια σχέση ισοδυναμίας στο ![]() .
.
(Στα Μαθηματικά, γενικά, μια διμελής σχέση, σ’ ένα σύνολο ![]() , ορίζεται ένα σύνολο διατεταγμένων ζευγών
, ορίζεται ένα σύνολο διατεταγμένων ζευγών ![]() , με
, με ![]() . Πολλές φορές για να δηλώσουμε ότι ένα ζεύγος
. Πολλές φορές για να δηλώσουμε ότι ένα ζεύγος ![]() είναι στοιχείο της σχέσης,
είναι στοιχείο της σχέσης, ![]() , σημειώνουμε
, σημειώνουμε ![]() . Μια διμελής σχέση, στο
. Μια διμελής σχέση, στο ![]() , καλείται σχέση ισοδυναμίας όταν πληροί τις εξής τρεις ιδιότητες:
, καλείται σχέση ισοδυναμίας όταν πληροί τις εξής τρεις ιδιότητες:
-
Την ανακλαστική, δηλαδή,
 , για κάθε
, για κάθε 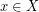
-
Τη συμμετρική, δηλαδή, αν
 , τότε,
, τότε, 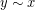 για κάθε
για κάθε 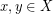
-
Τη μεταβατική, δηλαδή, αν
 και
και 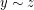 , τότε,
, τότε,  , για κάθε
, για κάθε 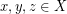 .)
.)
Επιπλέον, για κάθε συνάρτηση ![]() , ορίζουμε το σύνολο,
, ορίζουμε το σύνολο,
![]()
(Το ![]() απαρτίζεται από εκείνα τα στοιχεία,
απαρτίζεται από εκείνα τα στοιχεία, ![]() , του
, του ![]() που συνδέονται με τη
που συνδέονται με τη ![]() , μέσω της σχέσης
, μέσω της σχέσης ![]() . Το σύνολο αυτό λέγεται κλάση ισοδυναμίας του
. Το σύνολο αυτό λέγεται κλάση ισοδυναμίας του ![]() .)
.)
Έστω,
![]()
το σύνολο όλων των συνόλων, της μορφής, ![]() , για τις διάφορες συναρτήσεις
, για τις διάφορες συναρτήσεις ![]() .
.
(Το ![]() απαρτίζεται από όλες τις δυνατές κλάσεις ισοδυναμίας της σχέσης
απαρτίζεται από όλες τις δυνατές κλάσεις ισοδυναμίας της σχέσης ![]() στο
στο ![]() . Το σύνολο αυτό λέγεται σύνολο πηλίκο.)
. Το σύνολο αυτό λέγεται σύνολο πηλίκο.)
Θεωρούμε, τώρα, την απεικόνιση,
![]()
που ορίζεται από τον τύπο,
![]()
Πρώτα απ’ όλα, η ![]() είναι καλώς ορισμένη:
είναι καλώς ορισμένη:
Πραγματικά, αν ![]() , τότε, αφού,
, τότε, αφού,
![]()
θα είναι,
![]()
επομένως, ![]() , συνεπώς,
, συνεπώς,
![]()
Θα αποδειχτεί, πλέον, ότι αυτή η αντιστοιχία συνδέει με αμφιμονοσήμαντο τρόπο τα στοιχεία των συνόλων ![]() και
και ![]() :
:
Για το σκοπό αυτό, έστω, ![]() . Από τον ορισμό του
. Από τον ορισμό του ![]() , θα υπάρχει
, θα υπάρχει ![]() με
με ![]() , οπότε,
, οπότε,
![]()
Από την άλλη μεριά, έστω,
![]()
όπου ![]() .
.
Προφανώς, ![]() , άρα
, άρα ![]() .
.
Συμπερασματικά, κάθε στοιχείο του ![]() μπορεί να απεικονιστεί, μέσω της
μπορεί να απεικονιστεί, μέσω της ![]() , στο αντίστοιχο στοιχείο του στο
, στο αντίστοιχο στοιχείο του στο ![]() .
.
Για καθε ![]() , συμβολίζουμε,
, συμβολίζουμε,
![]()
Αν υποτεθεί ότι ![]() , όπου
, όπου ![]() , τότε, εύκολα, συνάγεται ότι,
, τότε, εύκολα, συνάγεται ότι,
![]()
Αντιλαμβάνεστε, τώρα, τι εννοούμε όταν, συμβατικά, γράφουμε ότι,
![]()
όπου ![]() μια αρχική της
μια αρχική της ![]() ;
;
Στην πραγματικότητα, επιλέγουμε έναν “αντιπρόσωπο” από το σύνολο ![]() .
.
Η παρουσία της σταθεράς ![]() , αν και στερείται ουσιαστικού μαθηματικού περιεχομένου, υπενθυμίζει τη φύση της έννοιας του
, αν και στερείται ουσιαστικού μαθηματικού περιεχομένου, υπενθυμίζει τη φύση της έννοιας του ![]() .
.
Για παράδειγμα, οι συμβατικές ισότητες,
![]()
είναι εξίσου σωστές, άρα κι οι συνεπακόλουθες,
![]()
Για να γίνει περισσότερο “λειτουργική” αυτή η αντιστοιχία, το ![]() μπορεί να εφοδιαστεί με δύο πράξεις.
μπορεί να εφοδιαστεί με δύο πράξεις.
Συγκεκριμένα, για κάθε ![]() , ορίζουμε,
, ορίζουμε,
![]()
και για κάθε ![]() και
και ![]() , ορίζουμε,
, ορίζουμε,
![]()
Όπως προηγουμένως, αποδεικνύεται ότι οι πράξεις αυτές είναι καλώς ορισμένες.
(Ακόμη, μπορούν να αποδειχτούν και οι αντίστοιχες ιδιότητες των πράξεων, της πρόσθεσης και του πολλαπλασιασμού αριθμού επί διάνυσμα, από το χώρο των διανυσμάτων. Για το λόγο αυτό το ![]() αποτελεί διανυσματικό χώρο.)
αποτελεί διανυσματικό χώρο.)
Επιπλέον, αποδεικνύεται ότι,
![]()
για κάθε ![]() και για κάθε
και για κάθε ![]() .
.
Πράγματι,
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} \displaystyle T\big(\lambda *[{{g}_{1}}]\oplus \mu *[{{g}_{2}}]\big)&=T\big([\lambda \cdot {{g}_{1}}]\oplus [\mu \cdot {{g}_{2}}]\big)\\ &=T\big([\lambda \cdot {{g}_{1}}+\mu \cdot {{g}_{2}}]\big)\\ &=\left({\lambda \cdot {{g}_{1}}+\mu \cdot {{g}_{2}}} \right)'\\ &=\lambda\cdot g{{'}_{1}}+\mu \cdot g{{'}_{2}}\\ &=\lambda\cdot T\big([{{g}_{1}}]\big)+\mu \cdot T\big([{{g}_{2}}]\big). \end{aligned} \end{equation*}](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-74257e8dcc7278e008b7f0024a2a5ecf_l3.png?x32006)
Ίσως, ο συμβολισμός να είναι λίγο αποθαρρυντικός, ωστόσο, η (3) εκφράζει τη γραμμικότητα της παραγώγισης, (να παρατηρήσετε την 3η και 4η από τις παραπάνω ισότητες), ενώ μέσω της (3), οι (1), (2) εκφράζουν, αντίστοιχα, τις γνωστές ιδιότητες του ολοκληρώματος,
![]()
και
![]()
Γενικότερα, η ισότητα,
![]()
για κάθε ![]() και για κάθε
και για κάθε ![]() ,
,
εκφράζει τη γραμμικότητα της αντιπαραγώγισης,
![]()
