Εξισώσεις α΄ βαθμού

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 21-07-2018

Οι εξισώσεις, στη συνείδηση των περισσότερων μαθητών, είναι συνυφασμένες με τα ίδια τα Μαθηματικά και, σίγουρα, η ανάκλησή τους δεν προκαλεί, πάντοτε, τα πιο ευχάριστα συναισθήματα …

Αλλά, κι έξω απ’τον εκπαιδευτικό χώρο μπορεί, συχνά, κανείς να ακούσει να γίνεται λόγος γι’ αυτό το βαρύγδουπο φορτίο της σχολικής ζωής. Πλέον, συνήθως, είναι επιφορτισμένο να διαδραματίσει το ρόλο ενός μέτρου σύγκρισης για το βαθμό πολυπλοκότητας ενός προβλήματος, ή το βαθμό της δυσκολίας ενός εγχειρήματος, καθώς και να συσχετιστεί με τον απαιτητικό χαρακτήρα μιας προσπάθειας.

Απ’ τη μια πλευρά, αυτή η διαπίστωση  φανερώνει την εντύπωση που προκαλεί η ενότητα αυτή, ενώ, από την άλλη, εγείρει αρκετούς προβληματισμούς καταδεικνύοντας την ύπαρξη εγγενών αδυναμιών και ιδιαιτεροτήτων κατά τη διδακτική προσέγγιση.

Η χρησιμότητα της εξοικείωσης με ορισμένες απλές εξισώσεις πρώτου βαθμού, μάλλον, είναι αδιαπραγμάτευτη, ακόμη και για τους μικρότερους μαθητές, και η αντιμετώπιση ορισμένων προβλημάτων, από διάφορα πεδία, με το συστηματικό τρόπο που προσφέρουν, ίσως να πείσει και τον πιο δύσπιστο για την αδιαμφισβήτητη αξία τους.

Ωστόσο, το κεφάλαιο των εξισώσεων φαίνεται πολύπλοκο, στους μικρούς μαθητές του Γυμνασίου, διότι προϋποθέτει, πρώτα απ΄όλα, την κατανόηση της βασικής ορολογίας που το συνοδεύει, όπως α’ και β’ μέλος, γνωστές ποσότητες και άγνωστες ποσότητες, συντελεστής του αγνώστου, απαλοιφή παρονομαστών, απλοποίηση, επιμεριστική ιδιότητα, αναγωγή όμοιων όρων.

Στη συνέχεια, απαιτεί αναγνώριση των συμβολισμών και μια σχετική ευχέρεια κατά την εκτέλεση των μαθηματικών διεργασιών που επίκεινται με βάση τη μορφή της εξίσωσης. Στους αλγεβρικούς χειρισμούς περιλαμβάνονται ο  πολλαπλασιασμός όλων των όρων μιας εξίσωσης με το ΕΚΠ των παρονομαστών, που παρουσιάζονται, η εφαρμογή των απλοποιήσεων και της επιμεριστικής ιδιότητας, η αναγωγή όμοιων όρων, η  επιλογή, μεταφορά και η απόθεση όρων, από το ένα μέλος στο άλλο, με την ταυτόχρονη αλλαγή του προσήμου τους. Όλα αυτά υφαίνουν το σύνθετο χαρακτήρα του και δικαιολογούν, τροποντινά, κάποιες αστοχίες που παρατηρούνται κατά τον απολογισμό της διδασκαλίας του κεφαλαίου.

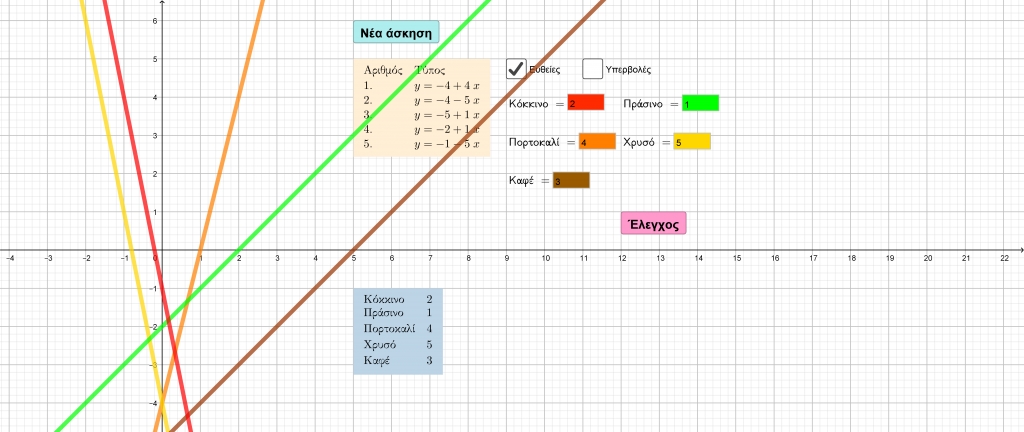
Στη διαδραστική εφαρμογή, που ακολουθεί, μπορείτε, υποστηρικτικά, να εξασκηθείτε με διάφορες εξισώσεις πρώτου βαθμού και με τις αντίστοιχες μεθόδους επίλυσής τους. Ίσως, να προσφέρεται, έτσι, ένας εναλλακτικός τρόπος διαπραγμάτευσης του συγκεκριμένου θέματος, με τα ενδιαφέροντα χαρακτηριστικά που ενσωματώνει η ψηφιακή προσέγγιση. 

 

Διαβάστε περισσότερα

Ο αλγόριθμος υπολογισμού τετραγωνικής ρίζας

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 28-06-2018

Μετά από κάποια εισαγωγικά μαθήματα σχετικά με την έννοια της τετραγωνικής ρίζας και με τον υπολογισμό κάποιων ειδικών περιπτώσεων τετραγωνικών ριζών, δοκιμάζοντας αριθμούς ωσότου βρεθεί αυτός του οποίου το τετράγωνο, δηλαδή το γινόμενό του επί τον εαυτό του, ισούται με την υπόρριζη ποσότητα, είναι εύλογο να αναρωτηθεί κανείς αν υπάρχει κάποια γενικότερη μέθοδος υπολογισμού τετραγωνικών ριζών. Η απάντηση είναι καταφατική και, στη συνέχεια, επιχειρείται, με τη βοήθεια ενός παραδείγματος, μια πρώτη γνωριμία με τη μέθοδο αυτή.

Θα βρεθεί η τετραγωνική ρίζα του αριθμού 119025.

    1. Τα ψηφία του χωρίζονται, ανά δύο, από δεξιά: 11\left| {90} \right.\left| {25} \right. και ο αριθμός τοποθετείται, πάνω αριστερά, σε μια διάταξη παρόμοια μ’ αυτήν που χρησιμοποιείται κατά την εφαρμογή του αλγόριθμου της διαίρεσης.

          \[$ \displaystyle \left. {\begin{array}{*{20}{c}} {\ \ \ 11} & {90} & {25} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{...............}}} \\ {\text{ }...............} \end{array}$\]

    2. Βρίσκουμε τον αριθμό (3) ο οποίος όταν υψωθεί στο τετράγωνο προσεγγίζει, όσο το δυνατόν περισσότερο, χωρίς, όμως, να υπερβαίνει τον πρώτο, από αριστερά αριθμό, μετά τον χωρισμό ({{3}^{2}}=9<11). Τον αριθμό που βρήκαμε τον γράφουμε πάνω δεξιά στην προαναφερόμενη διάταξη.

          \[ \displaystyle \left. {\begin{array}{*{20}{c}} {\ \ \ 11} & {90} & {25} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........}}} \\ {\text{ }...............} \end{array}$\]

    3. Το τετράγωνο του αριθμού, που βρήκαμε στο προηγούμενο βήμα, αφαιρείται από τον πρώτο, από αριστερά αριθμό, μετά τον χωρισμό, σημειώνοντας το αποτέλεσμα, ως ακολούθως,

          \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ {...............} \\ {} \end{array}$\]

    4. Προσαρτούμε τον επόμενο, από αριστερά, αριθμό, μετά τον χωρισμό, (90) δεξιά του αποτελέσματος, του προηγούμενου βήματος (2).

          \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ {...............} \\ {} \end{array}$\]

    5. Διπλασιάζουμε τον αριθμό, που υπάρχει πάνω δεξιά, στην προηγούμενη διάταξη, (3), σημειώνοντας το αποτέλεσμα (6), κάτω δεξιά της. 

          \[ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ 6 \\ {} \end{array}$\]

      Πλέον, αναζητείται το ψηφίο (4) το οποίο, δίπλα στο προηγούμενο αποτέλεσμα, (6), στη θέση των μονάδων, σχηματίζει έναν αριθμό (64) ο οποίος πολλαπλασιαζόμενος επί το ζητούμενο ψηφίο (4) προσεγγίζει, όσο το δυνατόν περισσότερο, χωρίς, όμως, να υπερβαίνει το αποτέλεσμα που βρέθηκε στο βήμα 4 (4\cdot 64=256<290).

          \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{3\text{ }...........\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \end{array}$\]

      Το ψηφίο αυτό σημειώνεται δεξιά του αποτελέσματος που βρέθηκε στο βήμα 2.

          \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \end{array}$\]

    6. Το αποτέλεσμα του γινομένου, όπως περιεγράφηκε στο βήμα 5, αφαιρείται από τον αριθμό που είχε βρεθεί στο βήμα 4, όπως παρακάτω,

          \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \\ {} \end{array}$\]

    7. Επαναλαμβάνουμε τα βήματα 4-6, ωσότου «εξαντληθεί» η υπόρριζη ποσότητα, προχωρώντας, αν χρειαστεί, παρόμοια, και στο δεκαδικό της μέρος, πάντοτε σε σχέση και με την επιζητούμενη ακρίβεια.   

          \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \\ {} \end{array}$\]

                                 

          \[$\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \end{array}$\]

                                                                                       

          \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{345\text{ }..\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \end{array}$\]

                                                                                        

          \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \\ {} & {} & {\underline{{\begin{array}{*{20}{c}} - & {3425} \end{array}}}} & {} \\ {} & {} & {\begin{array}{*{20}{c}} {} & 0 \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{\text{ }345\text{ }\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \\ {} & {} \\ {} & {} \end{array}$\]

    8. Το εξαγόμενο της ρίζας, για τη ζητούμενη ακρίβεια, είναι ο αριθμός που βρίσκεται πάνω δεξιά στη χρησιμοποιούμενη διάταξη,

          \[$ \displaystyle \sqrt{{119025}}=345$.\]

Για να εμβαθύνουμε, περισσότερο, στον αλγόριθμο, ας επιχειρήσουμε να εκτιμήσουμε τη \displaystyle \sqrt{{119025}}, από μικρότερες τιμές.

  • Με προσέγγιση εκατοντάδων: Επειδή, \displaystyle {{300}^{2}}=90000<119025, ενώ, \displaystyle {{400}^{2}}=160000>119025, έχουμε ότι, \displaystyle \sqrt{{119025}}\approx 300. Έτσι, προκύπτει το ψηφίο \displaystyle 3 στο βήμα 2. Βέβαια, εκεί η διαδικασία παρουσιάστηκε απλοποιημένη, διότι, ουσιαστικά,

        \[$ \displaystyle {{3}^{2}}=9<11<11,9025$,\]

    ενώ,

        \[$ \displaystyle {{4}^{2}}=16>11,9025$\]

    (Τροποντινά, τα μηδενικά του \displaystyle 300 αποσιωπώνται, στο βήμα 2, αφού, άλλωστε, στην πορεία, ενδεχομένως, να αντικατασταθούν από άλλα ψηφία, καθώς, η προσέγγιση βελτιώνεται.)

  • Με προσέγγιση δεκάδων: Επειδή,

        \[$\displaystyle {{340}^{2}}=115600<119025$,\]

    ενώ,

        \[$\displaystyle {{350}^{2}}=122500>119025$,\]

    έχουμε ότι, \displaystyle \sqrt{{119025}}\approx 340.

    Έτσι, προκύπτει το ψηφίο \displaystyle 4 στο βήμα 5. Βέβαια, εκεί η διαδικασία παρουσιάστηκε με αμεσότερο τρόπο και υποστηρίχθηκε από ένα συμπέρασμα, που αναφέρεται στη διαφορά δύο τετραγώνων, το οποίο θα σκιαγραφηθεί αμέσως παρακάτω. Στα ακόλουθα σχήματα,                                                                                                                                                                                                                                                                                                                         

    ερμηνεύεται, γεωμετρικά, η ισότητα,

        \[$ \displaystyle {{340}^{2}}-{{300}^{2}}=\left( {340-300} \right)\left( {340+300} \right)$\]

    η οποία γράφεται,

        \[$ \displaystyle {{340}^{2}}-{{300}^{2}}=40\cdot 640$\]

    (Τροποντινά, το γινόμενο \displaystyle 40\cdot 640 βελτιώνει, προσθετικά, την αρχική προσέγγιση του \displaystyle {{300}^{2}} για την υπόρριζη ποσότητα. Γι’ αυτό, αποσιωπώντας τα μηδενικά, αναζητείται εκ των προτέρων, στη θέση των δεκάδων της εκτίμησης  της ρίζας, το ψηφίο 4 το οποίο, δίπλα στο 2\cdot 3=6, στη θέση των μονάδων, σχηματίζει τον αριθμό 64 ο οποίος πολλαπλασιαζόμενος επί το ψηφίο 4 προσεγγίζει, όσο το δυνατόν περισσότερο, χωρίς, όμως, να υπερβαίνει το αποτέλεσμα που προκύπτει αν στη διαφορά \displaystyle 11-{{3}^{2}}=2 προσαρτηθεί το επόμενο ζεύγος ψηφίων (90) της υπόρριζης ποσότητας.)

  • Με προσέγγιση μονάδων. Το ίδιο σκεπτικό, που περιεγράφηκε προηγουμένως, οδηγεί στο ψηφίο 5,

    διότι,

        \[$ 290-4\cdot 64=290-256=34$\]

    ενώ,

        \[$ 685\cdot 5=3425$,\]

    δηλαδή, ακριβώς ο αριθμός που προκύπτει αν προσαρτηθεί στο 34 το επόμενο ζεύγος ψηφίων (25) της υπόρριζης ποσότητας.

 

 

Διαβάστε περισσότερα

Η έννοια της συνάρτησης

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 06-01-2014

Στα ακόλουθα παραδείγματα, ένα μέγεθος σχετίζεται με κάποιο άλλο μέγεθος,

  • το κόστος αγοράς των ψαριών, στα ψαράδικα, είναι ανάλογο του βάρους τους.
  • ο μηνιαίος μισθός μιας πωλήτριας, σ΄ ένα μαγαζί με ρούχα, εξαρτάται απ΄ τις πωλήσεις ρούχων που πραγματοποίησε.
  • σε κάθε όχημα, η απόσταση φρεναρίσματος, έχει σχέση με την παλαιότητα των ελαστικών.
  • η πρόοδος ενός μαθητή είναι αποτέλεσμα της προσπάθειάς του.

Στα Μαθηματικά, η έννοια της συνάρτησης, για δύο μεγέθη, είναι συνυφασμένη με την έννοια της εξάρτησης του ενός από το άλλο. Φυσικά, η αποσαφήνιση της σχέσης εξάρτησης, μεταξύ δύο μεγεθών, δεν είναι, πάντοτε, απλή διαδικασία. Η αποτύπωση αυτής της σχέσης εξάρτησης, όταν επιτυγχάνεται, μπορεί να γίνει με διάφορους τρόπους, όπως με τη βοήθεια ενός μαθηματικού τύπου, του τύπου της συνάρτησης, είτε με τη βοήθεια ενός πίνακα τιμών των μεγεθών, είτε, τέλος, με τη βοήθεια ενός γραφήματος, της γραφικής παράστασης της συνάρτησης.

Παράδειγμα Α (Τύπος συνάρτησης): Το διάστημα , S, σε \roman{\text{km}}, που καλύπτει σε χρόνο t, σε \roman{\text{sec}}, ένα αυτοκίνητο, που κινείται με σταθερή ταχύτητα U=70 \roman{\text{ km/h}}, δίνεται από τον τύπο S=70t.   Θα μπορούσατε να κατασκευάσετε έναν πίνακα τιμών για ορισμένες ενδεικτικές τιμές του χρόνου ;

Παράδειγμα Β (Πίνακας τιμών συνάρτησης):

  • Ο μηνιαίος μισθός ενός υπαλλήλου καθορίζεται από κάποιο σταθερό μηνιάτικο στο οποίο προστίθεται ένα ποσοστό επί των πωλήσεων που πραγματοποιεί. Ο ακόλουθος πίνακας παριστάνει τους μισθούς του υπαλλήλου τους τελευταίους πέντε μήνες με βάση τις πωλήσεις που πραγματοποίησε.
     Πωλήσεις σε €   Μισθός σε €
    1000 600
    2000 700
    2500 750
    4000 900
    6000 1100
    Θα μπορούσατε να βρείτε αυτό το σταθερό μηνιάτικο καθώς και το ποσοστό τα οποία διαμορφώνουν τον μισθό;
  • Ο Δήμος Διρφύων – Μεσσαπίων πρόκειται να προσλάβει ορισμένους εργάτες για ένα έργο. Ο τελικός αριθμός των εργατών θα εξαρτηθεί από τις ημέρες που θα χρειαστούν να ολοκληρώσουν το έργο. Ο Δήμος απευθύνθηκε σε μία εταιρία στην Χαλκίδα, η οποία, στο πλαίσιο της προσφοράς της, έδωσε τις εξής πληροφορίες:
     Αριθμός εργατών 
    		  Ημέρες εργασίας
    5 60
    10 30
    20 15
    30 10

    Θα μπορούσατε να βρείτε τις ημέρες εργασίας που θα χρειάζονταν 12 εργάτες;

Παράδειγμα Γ (Γραφική παράσταση συνάρτησης): Στο ακόλουθο γράφημα παριστάνεται η πρόγνωση για την ταχύτητα, σε μποφόρ, του ανέμου στην περιοχή της Χαλκίδας, κάποιες ημέρες του Ιανουαρίου 2014, από το meteo.gr.

meteo_Chalkis

Θα μπορούσατε να βρείτε πότε αναμένεται η ελάχιστη και πότε η μέγιστη τιμή του ανέμου, καθώς και τις αντίστοιχες τιμές; Ποιες είναι οι σταθερές, κατά διαστήματα, τιμές του ανέμου;

Μια σημαντική κατηγορία συναρτήσεων είναι αυτή που περιλαμβάνει τις σχέσεις που καθορίζουν τον τρόπο συσχέτισης δύο ανάλογων ποσών (όπως το διάστημα, S, και ο χρόνος, t, στο Παράδειγμα Α) ή δύο ποσών που οι μεταβολές τους είναι ανάλογες (όπως η αύξηση του μισθού του υπαλλήλου στο Παράδειγμα Β1 σε σχέση με την αύξηση των πωλήσεων που πραγματοποίησε). Πρόκειται για τις επονομαζόμενες Γραμμικές Συναρτήσεις, αφού η γραφική τους αναπαράσταση είναι ευθεία γραμμή.

Δεύτερη σημαντική κατηγορία συναρτήσεων είναι αυτή που περιλαμβάνει τις σχέσεις που καθορίζουν τον τρόπο συσχέτισης δύο αντιστρόφως ανάλογων ποσών (όπως ο αριθμός των εργατών σε σχέση με τις ημέρες εργασίας στο Παράδειγμα Β2). Πρόκειται για συναρτήσεις με γραφικές παραστάσεις καμπύλες που ονομάζονται υπερβολές.

Το ακόλουθο διαδραστικό παιχνίδι αναφέρεται σ΄ αυτές τις δύο κατηγορίες συναρτήσεων.


Διαβάστε περισσότερα

Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH