Καρδιοειδής καμπύλη

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Α΄ Λυκείου, Άλγεβρα Β΄ Λυκείου, Γεωμετρία Α΄ Λυκείου, Για τη Β΄ Λυκείου, Για την Α΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 11-05-2019

Από προηγούμενες τάξεις, έχει γίνει φανερό ότι, με τη βοήθεια κατάλληλων συστημάτων συντεταγμένων, διάφορα γεωμετρικά αντικείμενα μπορούν να περιγραφούν με τη βοήθεια εξισώσεων. Για παράδειγμα, η εξίσωση y=\alpha x +\beta παριστάνει ευθεία, η εξίσωση y=\alpha x^2,\,\alpha\neq0 παριστάνει παραβολή, η εξίσωση y=\frac{\alpha}{x},\,\alpha,\,x\neq0 παριστάνει υπερβολή κ. ά..

Ωστόσο, ίσως να μην έχει γίνει απόλυτα κατανοητός ο τρόπος με τον οποίο ένα γεωμετρικό αντικείμενο θα μπορούσε να μετασχηματιστεί σε κάποιο άλλο γεωμετρικό αντικείμενο. Ενδεικτικά, πως μια ευθεία μπορεί να μετασχηματιστεί σε μια άλλη ευθεία, με διαφορετική κλίση; Πως μια παραβολή μπορεί να μετασχηματιστεί σε μια νέα παραβολή, περισσότερο ή λιγότερο κλειστή; Πως ένας κύκλος μπορεί να μετασχηματιστεί σ’ έναν “πεπλατυσμένο” ή “επιμηκυμένο” κύκλο (έλλειψη) ή, προχωρώντας λίγο πιο πέρα, πως μπορεί να μετασχηματιστεί σε μια “καρδιά”;

Ενδεχομένως, τα προηγούμενα ερωτήματα να συνδέονται και να είναι απλώς διαφορετικές πτυχές του ίδιου προβλήματος.

Αξίζει, λοιπόν, να προβληματιστεί κανείς πάνω στις αλλαγές που θα έπρεπε να συντελεστούν στους τύπους των αντίστοιχων εξισώσεων οι οποίες θα μπορούσαν να επιφέρουν αυτούς τους μετασχηματισμούς.

Ενδιαφέρον, βέβαια, παρουσιάζει και το αντίστροφο ερώτημα:

Τι αντίκτυπο, λόγου χάρη, θα είχε στη διχοτόμο του πρώτου και τρίτου τεταρτημορίου, δηλαδή στην ευθεία με εξίσωση y=x, μια “παρέμβαση” στον προηγούμενο τύπο, θέτοντας όπου x το 2x;

Αλγεβρικά, προφανώς, θα είχαμε την εξίσωση y=2x, η οποία αναπαριστά μια νέα ευθεία, ωστόσο, πως αυτό θα μπορούσε να ερμηνευτεί γεωμετρικά συσχετίζοντας τις δύο ευθείες; Φαίνεται, λοιπόν, ότι, σε μια τέτοια περίπτωση, ο άξονας των y “διαστέλλεται” συμπαρασύροντας τα σημεία της ευθείας y=x στις νέες θέσεις τους πάνω στην ευθεία y=2x. Τροποντινά, αλλάζει η κλίμακα των αξόνων και η αλλαγή αυτή κατευθύνεται από την αναλογία 1:2.

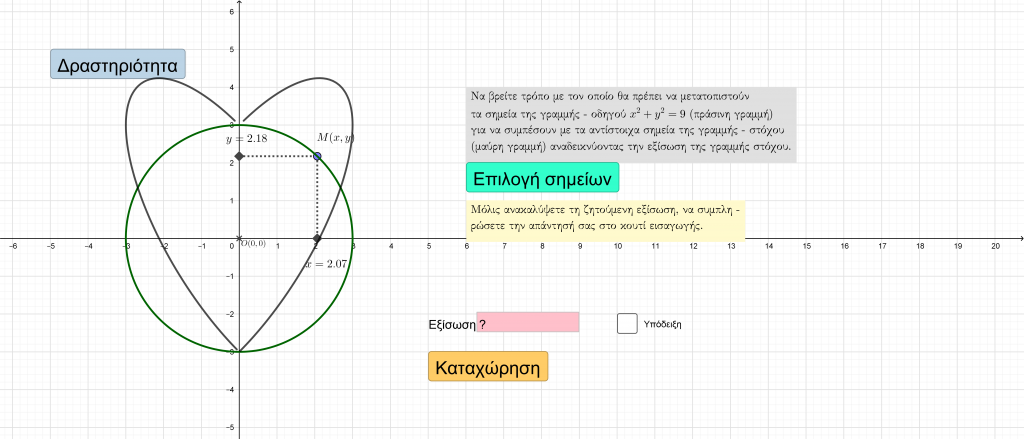
Απώτερος στόχος της διαδραστικής εφαρμογής που ακολουθεί είναι να σας βοηθήσει στην εύρεση της εξίσωσης μιας καμπύλης που το σχήμα της μοιάζει με το σχήμα της καρδιάς.  Όπως θα δείτε, ο συγκεκριμένος τύπος του καρδιοειδούς θα μπορούσε να ανακύψει “τροποποιώντας”, κατάλληλα, έναν “εύπλαστο” κύκλο, αναδεικνύοντας, έτσι, την αντίστοιχη εξίσωση. Βέβαια, απαραίτητη προϋπόθεση είναι η γνώση της εξίσωσης του κύκλου, η οποία στην ειδική περίπτωση του κύκλου (O,\rho), αποδεικνύεται, εύκολα, με χρήση του Πυθαγόρειου Θεωρήματος, ότι είναι x^2+y^2=\rho^2.

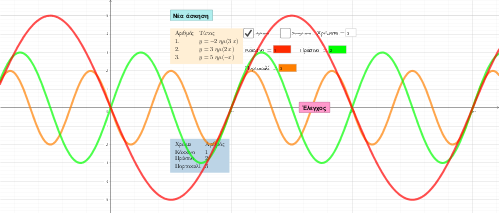
Όμως, προτού φτάσετε στο σημείο να αναζητήσετε την εξίσωση του καρδιοειδούς, θα έχετε τη δυνατότητα να εξασκηθείτε πάνω στην κεντρική ιδέα της μεθόδου με απλούστερους μετασχηματισμούς, για ορισμένες βασικές γραμμές , με αφετηρία την ευθεία.

Διαβάστε περισσότερα

Παράγωγος συνάρτησης σε σημείο του πεδίου ορισμού της

0

Συγγραφέας: dkonas | Κατηγορία Για την Γ΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Γ΄ Λυκείου, Μαθηματικά και Στοιχεία Στατιστικής Γ΄ Λυκείου | , στις 14-10-2018

Σε προηγούμενες τάξεις, είχατε συναντήσει την έννοια της εφαπτομένης, αρχικά, σε σημείο κύκλου, ενώ, στη συνέχεια, για τις υπόλοιπες κωνικές τομές, δηλαδή, για την έλλειψη, για την παραβολή και για την υπερβολή. Σε κάθε περίπτωση, η εφαπτομένη σ’ ένα σημείο μιας καμπύλης, απ’ τις παραπάνω, επιτυγχάνει να “πλησιάσει” την καμπύλη, τουλάχιστον, “κοντά” στο σημείο από το οποίο διέρχεται.

Το γεγονός ότι η απλούστερη γραμμή, δηλαδή, η ευθεία, θα μπορούσε να χρησιμοποιηθεί, μέσω της έννοιας της εφαπτομένης, για να προσεγγίσει ένα πιο σύνθετο, μη ευθύγραμμο σχήμα, όπως ο κύκλος, ή οι υπόλοιπες κωνικές τομές, αποτελεί κίνητρο, έτσι, ώστε, η έννοια αυτή να γενικευτεί και στις περιπτώσεις καμπυλών όπου μπορούν να θεωρηθούν γραφήματα συναρτήσεων τα οποία πληρούν μια συγκεκριμένη συνθήκη.

Όμως, ποια θα μπορούσε να είναι αυτή η συνθήκη και γιατί η εξασφάλισή της αποτελεί ικανό παράγοντα για να ορίζεται η εφαπτομένη; Ακόμη, πως θα μπορούσε να προσδιοριστεί η εφαπτομένη, μέσα από την προηγούμενη συνθήκη, δεδομένου ότι μια ευθεία μπορεί να οριστεί μέσω του συντελεστή διεύθυνσής της όταν είναι γνωστό ένα σημείο από το οποίο διέρχεται;

Η ακόλουθη διαδραστική εφαρμογή, διαπραγματεύεται τον ορισμό της εφαπτομένης σε σημείο A(x_0,f(x_0)) του γραφήματος, για μια συνάρτηση f, η οποία πληροί τη συνθήκη αυτή στο σημείο x_0 του πεδίου ορισμού της. Ενδεχομένως, με τη βοήθειά των διαδραστικών χαρακτηριστικών που παρέχει το γραφικό της περιβάλλον, να γίνει περισσότερο κατανοητή τόσο η συνθήκη όσο και η τεκμηρίωσή της, σε συγκεκριμένα παραδείγματα συναρτήσεων, καθώς και η σύνδεσή της με την εφαπτομένη της γραφικής παράστασης στο A(x_0,f(x_0)) των συναρτήσεων αυτών.

Σ’ ένα επόμενο βήμα, ίσως, να μπορούσε να βρεθεί και η εξίσωση που παριστάνει την εφαπτομένη αυτή, η οποία, σύμφωνα με τα παραπάνω, θεωρούμενη, κατάλληλα, ως συνάρτηση ισούται, κατά προσέγγιση, με την f, τουλάχιστον, για εκείνα τα x τα οποία βρίσκονται σε μια “περιοχή” του x_0.

Διαβάστε περισσότερα

Ρητές εξισώσεις

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Α΄ Λυκείου, Άλγεβρα Γ΄ Γυμνασίου, Για την Α΄ Λυκείου, Για την Γ΄ Γυμνασίου | , στις 23-08-2018

Όταν ο άγνωστος μιας εξίσωσης εμφανίζεται στον παρονομαστή ενός κλάσματος, τότε, η εξίσωση ονομάζεται κλασματική.

Στην ειδικότερη περίπτωση, όπου οι όροι της εξίσωσης έχουν ή μπορούν να πάρουν τη μορφή κλασμάτων, όπου τόσο ο αριθμητής όσο και ο παρονομαστής είναι πολυώνυμα, η εξίσωση λέγεται ρητή.

Κατά την επίλυση μιας ρητής εξίσωσης, αρχικά, καλό είναι να περιοριστεί το πεδίο αναζήτησης των λύσεών της, εξαιρώντας τις τιμές της μεταβλητής που μηδενίζουν τους εμφανιζόμενους παρονομαστές. Γι’ αυτό αποδεικνύεται, ιδιαίτερα, χρήσιμο οι παρονομαστές να έχουν προηγουμένως παραγοντοποιηθεί.  Η παραγοντοποίηση, άλλωστε, συμβάλλει στον υπολογισμό του ΕΚΠ των παρονομαστών, βήμα σημαντικό κατά τη μετέπειτα απαλοιφή τους. Πολλαπλασιάζοντας όλους τους όρους μιας κλασματικής εξίσωσης με το ΕΚΠ των παρονομαστών της, μετά την εκτέλεση των απλοποιήσεων που προκύπτουν, η αρχική εξίσωση μετασχηματίζεται σε πολυωνυμική εξίσωση όπου, στο πλαίσιο της Γ΄ Γυμνασίου, συνήθως, πρόκειται για μια εξίσωση πρώτου ή δεύτερου βαθμού.

Γενικά, είναι διαπιστωμένο ότι η ενότητα αυτή εμφανίζει σημαντικές δυσκολίες, κατά τη διδακτική προσέγγιση, αφού προϋποθέτει πλήρη κατανόηση για μια πληθώρα προ απαιτούμενων γνώσεων όπως ταυτότητες, παραγοντοποίηση, εύρεση ΕΚΠ, απλοποίηση, επιμεριστική ιδιότητα, αναγωγή όμοιων όρων, επίλυση εξισώσεων πρώτου και δεύτερου βαθμού.

Η διαδραστική εφαρμογή που ακολουθεί, πραγματεύεται τα παραπάνω θέματα για ποικίλες ρητές εξισώσεις παρέχοντας τη δυνατότητα ελέγχου των απαντήσεων του χρήστη αλλά και κάποιων κατευθυντήριων γραμμών μέσα από κατάλληλες υποδείξεις.

Διαβάστε περισσότερα

Εξισώσεις α΄ βαθμού

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 21-07-2018

Οι εξισώσεις, στη συνείδηση των περισσότερων μαθητών, είναι συνυφασμένες με τα ίδια τα Μαθηματικά και, σίγουρα, η ανάκλησή τους δεν προκαλεί, πάντοτε, τα πιο ευχάριστα συναισθήματα …

Αλλά, κι έξω απ’τον εκπαιδευτικό χώρο μπορεί, συχνά, κανείς να ακούσει να γίνεται λόγος γι’ αυτό το βαρύγδουπο φορτίο της σχολικής ζωής. Πλέον, συνήθως, είναι επιφορτισμένο να διαδραματίσει το ρόλο ενός μέτρου σύγκρισης για το βαθμό πολυπλοκότητας ενός προβλήματος, ή το βαθμό της δυσκολίας ενός εγχειρήματος, καθώς και να συσχετιστεί με τον απαιτητικό χαρακτήρα μιας προσπάθειας.

Απ’ τη μια πλευρά, αυτή η διαπίστωση  φανερώνει την εντύπωση που προκαλεί η ενότητα αυτή, ενώ, από την άλλη, εγείρει αρκετούς προβληματισμούς καταδεικνύοντας την ύπαρξη εγγενών αδυναμιών και ιδιαιτεροτήτων κατά τη διδακτική προσέγγιση.

Η χρησιμότητα της εξοικείωσης με ορισμένες απλές εξισώσεις πρώτου βαθμού, μάλλον, είναι αδιαπραγμάτευτη, ακόμη και για τους μικρότερους μαθητές, και η αντιμετώπιση ορισμένων προβλημάτων, από διάφορα πεδία, με το συστηματικό τρόπο που προσφέρουν, ίσως να πείσει και τον πιο δύσπιστο για την αδιαμφισβήτητη αξία τους.

Ωστόσο, το κεφάλαιο των εξισώσεων φαίνεται πολύπλοκο, στους μικρούς μαθητές του Γυμνασίου, διότι προϋποθέτει, πρώτα απ΄όλα, την κατανόηση της βασικής ορολογίας που το συνοδεύει, όπως α’ και β’ μέλος, γνωστές ποσότητες και άγνωστες ποσότητες, συντελεστής του αγνώστου, απαλοιφή παρονομαστών, απλοποίηση, επιμεριστική ιδιότητα, αναγωγή όμοιων όρων.

Στη συνέχεια, απαιτεί αναγνώριση των συμβολισμών και μια σχετική ευχέρεια κατά την εκτέλεση των μαθηματικών διεργασιών που επίκεινται με βάση τη μορφή της εξίσωσης. Στους αλγεβρικούς χειρισμούς περιλαμβάνονται ο  πολλαπλασιασμός όλων των όρων μιας εξίσωσης με το ΕΚΠ των παρονομαστών, που παρουσιάζονται, η εφαρμογή των απλοποιήσεων και της επιμεριστικής ιδιότητας, η αναγωγή όμοιων όρων, η  επιλογή, μεταφορά και η απόθεση όρων, από το ένα μέλος στο άλλο, με την ταυτόχρονη αλλαγή του προσήμου τους. Όλα αυτά υφαίνουν το σύνθετο χαρακτήρα του και δικαιολογούν, τροποντινά, κάποιες αστοχίες που παρατηρούνται κατά τον απολογισμό της διδασκαλίας του κεφαλαίου.

Στη διαδραστική εφαρμογή, που ακολουθεί, μπορείτε, υποστηρικτικά, να εξασκηθείτε με διάφορες εξισώσεις πρώτου βαθμού και με τις αντίστοιχες μεθόδους επίλυσής τους. Ίσως, να προσφέρεται, έτσι, ένας εναλλακτικός τρόπος διαπραγμάτευσης του συγκεκριμένου θέματος, με τα ενδιαφέροντα χαρακτηριστικά που ενσωματώνει η ψηφιακή προσέγγιση. 

 

Διαβάστε περισσότερα

Τα γραφήματα των κωνικών τομών

0

Συγγραφέας: dkonas | Κατηγορία Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 20-07-2018

Αναγνωρίζετε τις γραμμές των διάφορων κωνικών τομών;

Θα μπορούσατε να αντιστοιχίσετε διάφορα γραφήματα, κωνικών τομών, στις εξισώσεις τους;

Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, ίσως να επαναλάβετε ορισμένα βασικά συμπεράσματα της θεωρίας, σχετικά με τη μορφή αυτών των γραφημάτων και το πως σχετίζονται με τις εξισώσεις των αντίστοιχων κωνικών τομών.

 

 

Διαβάστε περισσότερα

Οι καμπύλες της εφαπτομένης και της συνεφαπτομένης

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 18-07-2018

Αναγνωρίζετε την καμπύλη της εφαπτομένης και της συνεφαπτομένης;

Θα μπορούσατε να αντιστοιχίσετε διάφορα γραφήματα, τέτοιων συναρτήσεων, στους τύπους τους;

Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, ίσως να επαναλάβετε ορισμένα βασικά συμπεράσματα της θεωρίας, σχετικά με τη μορφή αυτών των γραφικών παραστάσεων, σε συνδυασμό με τις γνωστές συμμετρίες, που προκύπτουν, για γραφήματα συναρτήσεων όπου οι τύποι τους συνδέονται με βάση συγκεκριμένες διεργασίες.

 

 

Διαβάστε περισσότερα

Ημιτονοειδείς και Συνημιτονοειδείς καμπύλες

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 18-07-2018

Αναγνωρίζετε τις καμπύλες των ημιτονοειδών και των συνημιτονοειδών συναρτήσεων;

Θα μπορούσατε να αντιστοιχίσετε διάφορα γραφήματα, τέτοιων συναρτήσεων, στους τύπους τους;

Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, ίσως να επαναλάβετε ορισμένα βασικά συμπεράσματα της θεωρίας, σχετικά με τη μορφή αυτών των γραφικών παραστάσεων, σε συνδυασμό με τις γνωστές συμμετρίες, που προκύπτουν, για γραφήματα συναρτήσεων όπου οι τύποι τους συνδέονται με βάση συγκεκριμένες διεργασίες.

 

Διαβάστε περισσότερα

Προηγούμενο
Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH