ΜαθηματιΚά

Ο αλγόριθμος υπολογισμού τετραγωνικής ρίζας

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 28-06-2018

Μετά από κάποια εισαγωγικά μαθήματα σχετικά με την έννοια της τετραγωνικής ρίζας και με τον υπολογισμό κάποιων ειδικών περιπτώσεων τετραγωνικών ριζών, δοκιμάζοντας αριθμούς ωσότου βρεθεί αυτός του οποίου το τετράγωνο, δηλαδή το γινόμενό του επί τον εαυτό του, ισούται με την υπόρριζη ποσότητα, είναι εύλογο να αναρωτηθεί κανείς αν υπάρχει κάποια γενικότερη μέθοδος υπολογισμού τετραγωνικών ριζών. Η απάντηση είναι καταφατική και, στη συνέχεια, επιχειρείται, με τη βοήθεια ενός παραδείγματος, μια πρώτη γνωριμία με τη μέθοδο αυτή.

Θα βρεθεί η τετραγωνική ρίζα του αριθμού $119025$ .

1. Τα ψηφία του χωρίζονται, ανά δύο, από δεξιά: 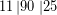$11\left| {90} \right.\left| {25} \right.$ και ο αριθμός τοποθετείται, πάνω αριστερά, σε μια διάταξη παρόμοια μ’ αυτήν που χρησιμοποιείται κατά την εφαρμογή του αλγόριθμου της διαίρεσης.
  
  $\displaystyle \left. {\begin{array}{*{20}{c}} {\ \ \ 11} & {90} & {25} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{...............}}} \\ {\text{ }...............} \end{array}$
2. Βρίσκουμε τον αριθμό ( $3$ ) ο οποίος όταν υψωθεί στο τετράγωνο προσεγγίζει, όσο το δυνατόν περισσότερο, χωρίς, όμως, να υπερβαίνει τον πρώτο, από αριστερά αριθμό, μετά τον χωρισμό ( ${{3}^{2}}=9<11$ ). Τον αριθμό που βρήκαμε τον γράφουμε πάνω δεξιά στην προαναφερόμενη διάταξη.
  
  $\displaystyle \left. {\begin{array}{*{20}{c}} {\ \ \ 11} & {90} & {25} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........}}} \\ {\text{ }...............} \end{array}$$
3. Το τετράγωνο του αριθμού, που βρήκαμε στο προηγούμενο βήμα, αφαιρείται από τον πρώτο, από αριστερά αριθμό, μετά τον χωρισμό, σημειώνοντας το αποτέλεσμα, ως ακολούθως,
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ {...............} \\ {} \end{array}$
4. Προσαρτούμε τον επόμενο, από αριστερά, αριθμό, μετά τον χωρισμό, ( 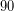$90$ ) δεξιά του αποτελέσματος, του προηγούμενου βήματος ( $2$ ).
  
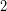  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ {...............} \\ {} \end{array}$
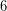5. Διπλασιάζουμε τον αριθμό, που υπάρχει πάνω δεξιά, στην προηγούμενη διάταξη, ( $3$ ), σημειώνοντας το αποτέλεσμα ( $6$ ), κάτω δεξιά της.
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ 6 \\ {} \end{array}$$
  
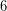  Πλέον, αναζητείται το ψηφίο ( $4$ ) το οποίο, δίπλα στο προηγούμενο αποτέλεσμα, ( $6$ ), στη θέση των μονάδων, σχηματίζει έναν αριθμό ( 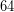$64$ ) ο οποίος πολλαπλασιαζόμενος επί το ζητούμενο ψηφίο ( $4$ ) προσεγγίζει, όσο το δυνατόν περισσότερο, χωρίς, όμως, να υπερβαίνει το αποτέλεσμα που βρέθηκε στο βήμα 4 ( $4\cdot 64=256<290$ ).
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{3\text{ }...........\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \end{array}$
  
  Το ψηφίο αυτό σημειώνεται δεξιά του αποτελέσματος που βρέθηκε στο βήμα 2.
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \end{array}$
6. Το αποτέλεσμα του γινομένου, όπως περιεγράφηκε στο βήμα 5, αφαιρείται από τον αριθμό που είχε βρεθεί στο βήμα 4, όπως παρακάτω,
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \\ {} \end{array}$
7. Επαναλαμβάνουμε τα βήματα 4-6, ωσότου «εξαντληθεί» η υπόρριζη ποσότητα, προχωρώντας, αν χρειαστεί, παρόμοια, και στο δεκαδικό της μέρος, πάντοτε σε σχέση και με την επιζητούμενη ακρίβεια.
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \\ {} \end{array}$
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \end{array}$
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{345\text{ }..\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \end{array}$
  
  $\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \\ {} & {} & {\underline{{\begin{array}{*{20}{c}} - & {3425} \end{array}}}} & {} \\ {} & {} & {\begin{array}{*{20}{c}} {} & 0 \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{\text{ }345\text{ }\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \\ {} & {} \\ {} & {} \end{array}$
8. Το εξαγόμενο της ρίζας, για τη ζητούμενη ακρίβεια, είναι ο αριθμός που βρίσκεται πάνω δεξιά στη χρησιμοποιούμενη διάταξη,
  
  $$ \displaystyle \sqrt{{119025}}=345$.$

Για να εμβαθύνουμε, περισσότερο, στον αλγόριθμο, ας επιχειρήσουμε να εκτιμήσουμε τη $\displaystyle \sqrt{{119025}}$ , από μικρότερες τιμές.

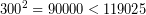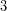Με προσέγγιση εκατοντάδων: Επειδή, $\displaystyle {{300}^{2}}=90000<119025$ , ενώ, $\displaystyle {{400}^{2}}=160000>119025$ , έχουμε ότι, $\displaystyle \sqrt{{119025}}\approx 300$ . Έτσι, προκύπτει το ψηφίο $\displaystyle 3$ στο βήμα 2. Βέβαια, εκεί η διαδικασία παρουσιάστηκε απλοποιημένη, διότι, ουσιαστικά,

$$ \displaystyle {{3}^{2}}=9<11<11,9025$,$

ενώ,

$\displaystyle {{4}^{2}}=16>11,9025$

(Τροποντινά, τα μηδενικά του 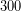$\displaystyle 300$ αποσιωπώνται, στο βήμα 2, αφού, άλλωστε, στην πορεία, ενδεχομένως, να αντικατασταθούν από άλλα ψηφία, καθώς, η προσέγγιση βελτιώνεται.)
Με προσέγγιση δεκάδων: Επειδή,

$$\displaystyle {{340}^{2}}=115600<119025$,$

ενώ,

$$\displaystyle {{350}^{2}}=122500>119025$,$

έχουμε ότι, $\displaystyle \sqrt{{119025}}\approx 340$ .

Έτσι, προκύπτει το ψηφίο $\displaystyle 4$ στο βήμα 5. Βέβαια, εκεί η διαδικασία παρουσιάστηκε με αμεσότερο τρόπο και υποστηρίχθηκε από ένα συμπέρασμα, που αναφέρεται στη διαφορά δύο τετραγώνων, το οποίο θα σκιαγραφηθεί αμέσως παρακάτω. Στα ακόλουθα σχήματα,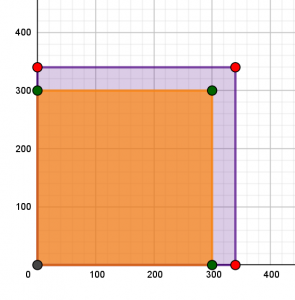

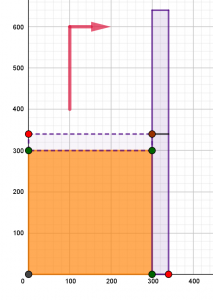
ερμηνεύεται, γεωμετρικά, η ισότητα,

$\displaystyle {{340}^{2}}-{{300}^{2}}=\left( {340-300} \right)\left( {340+300} \right)$

η οποία γράφεται,

$\displaystyle {{340}^{2}}-{{300}^{2}}=40\cdot 640$

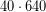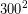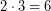(Τροποντινά, το γινόμενο $\displaystyle 40\cdot 640$ βελτιώνει, προσθετικά, την αρχική προσέγγιση του $\displaystyle {{300}^{2}}$ για την υπόρριζη ποσότητα. Γι’ αυτό, αποσιωπώντας τα μηδενικά, αναζητείται εκ των προτέρων, στη θέση των δεκάδων της εκτίμησης της ρίζας, το ψηφίο $4$ το οποίο, δίπλα στο $2\cdot 3=6$ , στη θέση των μονάδων, σχηματίζει τον αριθμό 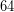$64$ ο οποίος πολλαπλασιαζόμενος επί το ψηφίο $4$ προσεγγίζει, όσο το δυνατόν περισσότερο, χωρίς, όμως, να υπερβαίνει το αποτέλεσμα που προκύπτει αν στη διαφορά $\displaystyle 11-{{3}^{2}}=2$ προσαρτηθεί το επόμενο ζεύγος ψηφίων ( $90$ ) 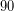της υπόρριζης ποσότητας.)
Με προσέγγιση μονάδων. Το ίδιο σκεπτικό, που περιεγράφηκε προηγουμένως, οδηγεί στο ψηφίο $5$ ,

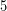διότι,

$290-4\cdot 64=290-256=34$

ενώ,

$$ 685\cdot 5=3425$,$

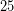δηλαδή, ακριβώς ο αριθμός που προκύπτει αν προσαρτηθεί στο $34$ το επόμενο ζεύγος ψηφίων ( $25$ ) της υπόρριζης ποσότητας.

Διαβάστε περισσότερα

Η “ρίζα” του – αναγκαίου – κακού …

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Α΄ Λυκείου, Γεωμετρία Α΄ Λυκείου, Για την Α΄ Λυκείου | , στις 04-09-2014

Θα μπορούσατε να τοποθετήσετε, κατάλληλα, τέσσερα ίδια τετράγωνα, χωρίς αλληλεπικαλύψεις, έτσι, ώστε να κατασκευάσετε ένα νέο τετράγωνο; Είναι δυνατόν να γίνει το ίδιο με εννιά ίδια τετράγωνα; Με δεκαέξι; Με δύο; Τι παρατηρείτε;

Ο όρος “τετραγωνική ρίζα”, για μια έννοια που συνήθως χρησιμοποιείται στο πλαίσιο αλγεβρικών διαδικασιών, έτσι κι αλλιώς, προϊδεάζει για δεσμούς της υπόστασής της με τη Γεωμετρία. Έχετε κάποια υπόννοια για το ποια θα μπορούσε να είναι η “ρίζα” ενός τετραγώνου;

Η σύνδεση με τη Γεωμετρία μπορεί να γίνει σχετικά εύκολα λ.χ. για τις τετραγωνικές ρίζες (τετράγωνων) αριθμών όπως το $4$ , το $9$ , το $16$ , το $25$ κλπ. Για παράδειγμα, για τον αριθμό $4$ , η τετραγωνική του ρίζα δεν είναι τίποτε άλλο παρά η πλευρά τετραγώνου με εμβαδό $4$ . Εναλλακτικά, πρόκειται για την πλευρά ενός τετραγώνου που έχει εμβαδό όσο το συνολικό εμβαδό τεσσάρων ίδιων τετραγώνων εμβαδού $1$ .

Στα αρχαία Ινδικά εγχειρίδια “Sulbasutra”, που αντλούν γνώσεις οι οποίες χρονολογούνται, ίσως, από το 2000 π.Χ. και μεταφέρθηκαν μέσω της προφορικής παράδοσης, περιγράφονται τρόποι κατασκευής βωμών και ναών, ενώ, ταυτόχρονα, δίνεται το απαραίτητο “τεχνικό” υπόβαθρο˙ μια συλλογή εμπειρικών “κανόνων” (“Sutra”), ουσιαστικά, από το πεδίο που αργότερα θα στοιχειοθετούσε τη “Γεωμετρία”. Προφανώς, σε κάποια από τις κατασκευές των αρχαίων Ινδών, χρειάστηκε ο υπολογισμός της διαγωνίου ενός τετραγώνου:

“Το μέτρο της πλευράς του πρέπει να αυξηθεί κατά το ένα τρίτο του κι αυτό (το ένα τρίτο του) ξανά με το ένα τέταρτό του μειωμένο κατά το τριακοστό τέταρτο (αυτού του τετάρτου)˙ αυτή είναι η διαγώνιος ενός τετραγώνου …”

Με σύγχρονη ορολογία και συμβολισμό:

$\sqrt{2}=1+\frac{1}{3}+\frac{1}{3\cdot4}-\frac{1}{3\cdot4\cdot34}\simeq 1.4142...,$

Αλήθεια πως ήταν σε θέση οι αρχαίοι Ινδοί να προσδιορίσουν με τόσο μεγάλη ακρίβεια την εύρεση του $\sqrt{2}$ ; Ποιές πρωταρχικές γεωμετρικές διαδικασίες θα μπορούσαν να έχουν αξιοποιήσει; Άραγε, κατά την προσέγγισή τους, να αντιλήφθηκαν την ιδιαιτερότητα έκφρασης αυτού του αριθμού;

Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής,

μπορείτε, ίσως, με μέθοδο παρόμοια μ΄ αυτήν που ενδεχομένως να ακολουθούσαν οι αρχαίοι Ινδοί, να βρείτε τρόπο έκφρασης των $\sqrt{2},\sqrt{3}$ και $\sqrt{5}$ .

Αναφορές

Henderson D.W., Square Roots in the Sulbasutra, Department of Mathematics, Cornell University.

Διαβάστε περισσότερα

Οι «ρίζες» … της τετραγωνικής ρίζας

0

Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Λυκείου, Για τη Β΄ Λυκείου | , στις 12-07-2012

Στην αρχαιότητα, η θεμελίωση και η νοηματοδότηση μιας μαθηματικής έννοιας επιτυγχάνοταν, συνήθως, μέσα από την απτή γεωμετρική της υπόσταση.

Η τετραγωνική ρίζα ενός αριθμού σήμαινε, ουσιαστικά, την πλευρά ενός τετραγώνου με εμβαδό ίσο με τον αριθμό. Φυσικά, μπορούσε, εύκολα, να κατασκευαστεί, γεωμετρικά, στις περιπτώσεις των (τετράγωνων) αριθμών $1$ , $4$ , $9$ , $16$ , $25$ , κ.ο.κ..

Επειδή κάθε αριθμός είναι γινόμενο δύο άλλων αριθμών, η γενική περίπτωση αναγόταν στην εύρεση της πλευράς του ισοδύναμου τετραγώνου ενός ορθογωνίου.

Στο δεύτερο βιβλίο των Στοιχείων του Ευκλείδη, συγκεκριμένα, στην Πρόταση 14, δίνεται ο τρόπος κατασκευής αυτού του τετραγώνου. Αν συμβολίσουμε τις διαστάσεις του ορθογωνίου με $\alpha, \beta$ , τότε πρόκειται, τροποντινά, για την κατασκευή του μέσου αναλόγου $x$ των ευθύγραμμων τμημάτων $\alpha, \beta$ . Άλλωστε,

$\dfrac{\alpha }{x}=\dfrac{x}{\beta }\Leftrightarrow x^{2}=\alpha \cdot \beta .$

Αλληλεπιδρώντας με το ακόλουθο γραφικό,

μπορείτε να δείτε τα βήματα της κατασκευής, η οποία παρουσιάζεται ελαφρώς τροποποιημένη σε σχέση με το βιβλίο των Στοιχείων. Αυτό έγινε, έτσι, ώστε να αναδειχθεί η βασική ιδέα της κατασκευής, αλλά και για να ενοποιηθούν οι επιμέρους προτάσεις των Στοιχείων που χρησιμοποιήθηκαν. Όπως θα διαπιστώσετε, μία από αυτές ήταν το Πυθαγόρειο Θεώρημα.

Ακόμη παλαιότερα, στο βιβλίο “Sulbasutram” γραμμένο στα Σανσκριτικά από τον Ινδό μαθηματικό Baudhayana, υπήρχε ένας διαφορετικός τρόπος κατασκευής αυτού του τετραγώνου. Ο τίτλος του βιβλίου, που χρονολογείται μεταξύ 800 και 600 π.Χ., μεταφράζεται ως “Κανόνες των σχοινιών”. Ήταν ένα εγχειρίδιο κατασκευών βωμών και ναών, όπου στο 1^ο Κεφάλαιο είχαν συγκεντρωθεί αριθμημένες γεωμετρικές προτάσεις επονομαζόμενες “Sutra”.

Η κατασκευή στηρίζεται στον Kανόνα 50 (Sutra 50), που, κι εδώ, δεν είναι τίποτε άλλο, παρά αυτό που, αργότερα, ονομάστηκε Πυθαγόρειο Θεώρημα. Αλληλεπιδρώντας με το ακόλουθο γραφικό,

μπορείτε να δείτε, ενοποιημένα, τα ενδιάμεσα στάδια της κατασκευής.

Αναφορές

Κέντρο έρευνας επιστήμης και εκπαίδευσης, Ευκλείδη Στοιχεία – Σύγχρονη απόδοση με εισαγωγή επεξηγήσεις και σχολιασμό – , Αθήνα 2001.
Henderson D.W., Geometric Solutions of quadratic and Cubic Equations, Department of Mathematics, Cornell University.

Διαβάστε περισσότερα

ΜαθηματιΚά Ένα ιστολόγιο του ΠΣΔ

Ο αλγόριθμος υπολογισμού τετραγωνικής ρίζας

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 28-06-2018

Η “ρίζα” του – αναγκαίου – κακού …

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Α΄ Λυκείου, Γεωμετρία Α΄ Λυκείου, Για την Α΄ Λυκείου | , στις 04-09-2014

Οι «ρίζες» … της τετραγωνικής ρίζας

0

Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Λυκείου, Για τη Β΄ Λυκείου | , στις 12-07-2012

Μήνυμα Διαχειριστή

Σελίδες

Ιστορικό

Σαν σήμερα

Μετάφραση

ΜαθηματιΚά Ένα ιστολόγιο του ΠΣΔ

Ο αλγόριθμος υπολογισμού τετραγωνικής ρίζας

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 28-06-2018

Η “ρίζα” του – αναγκαίου – κακού …

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Α΄ Λυκείου, Γεωμετρία Α΄ Λυκείου, Για την Α΄ Λυκείου | , στις 04-09-2014

Οι «ρίζες» … της τετραγωνικής ρίζας

0

Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Λυκείου, Για τη Β΄ Λυκείου | , στις 12-07-2012

Μήνυμα Διαχειριστή

Σελίδες

Ιστορικό

Σαν σήμερα

Μετάφραση

Ετικέτες