ΜαθηματιΚά Ένα ιστολόγιο του ΠΣΔ 

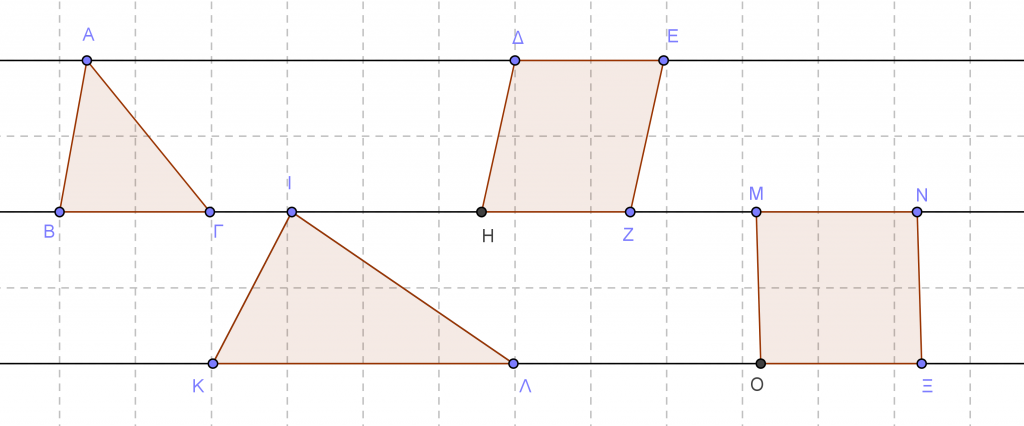
Γνωρίζετε, ήδη, τρόπους υπολογισμού εμβαδών ευθύγραμμων σχημάτων, όπως του τετραγώνου, του ορθογωνίου, του παραλληλογράμμου, του τριγώνου, του τραπεζίου.

Θα προσπαθήσουμε να ανακαλύψουμε έναν τρόπο για να υπολογίσουμε το εμβαδό του κυκλικού δίσκου. Η ιδιαιτερότητα του είναι ότι πρόκειται για καμπυλόγραμμο σχήμα. Μπορούμε, άραγε, να το “μετασχηματίσουμε” σ’ ένα ευθύγραμμο σχήμα με ίδιο εμβαδόν; Αν ναι, τότε, ενδεχομένως, να μπορούσαμε να υπολογίσουμε το εμβαδόν του.

Όμως, κάτι τέτοιο είναι αδύνατο. Ωστόσο, αυτό που μπορεί να γίνει είναι ο “μετασχηματισμός” του σ’ ένα σχήμα ίδιου εμβαδού, που προσεγγίζει ένα ευθύγραμμο σχήμα.

Όπως μπορείτε να παρατηρήσετε στο ακόλουθο γραφικό,

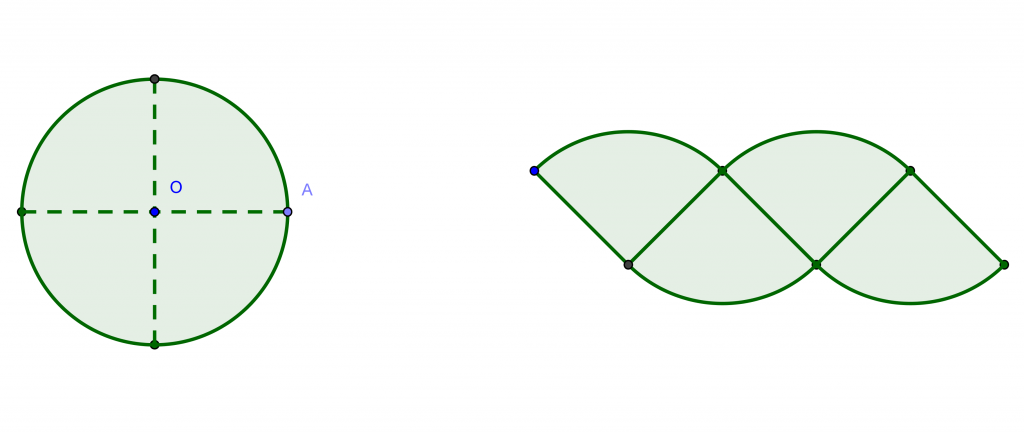
ο κυκλικός δίσκος έχει χωριστεί σε τέσσερις ίσους κυκλικούς τομείς, οι οποίοι έχουν τοποθετηθεί με τέτοιο τρόπο, ώστε να προκύπτει ένα σχήμα, το οποίο θα μπορούσε να χαρακτηριστεί ως “καμπυλόγραμμο παραλληλόγραμμο”. Προφανώς, το εμβαδόν του είναι το ίδιο με το εμβαδό του κυκλικού δίσκου.

Αν αλληλεπιδράσετε με το γραφικό αυτό, πατώντας το αριστερό πλήκτρο του ποντικιού σ’ ένα οποιοδήποτε σημείο του, θα παρατηρήσετε ότι όσο το πλήθος των κυκλικών τομέων αυξάνεται, τόσο το “καμπυλόγραμμο παραλληλόγραμμο” τείνει να γίνει ένα ορθογώνιο παραλληλόγραμμο, του οποίου οι διαστάσεις μπορούν να προσδιοριστούν.

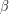Συγκεκριμένα, το “πλάτος” είναι όσο η ακτίνα του κύκλου και το “μήκος” όσο το μισό του μήκους του κύκλου, μιας και οι δύο “καμπυλόγραμμες πλευρές” του έχουν συνολικό μήκος όσο ο κύκλος. Επομένως, αν συμβολίσουμε με το μήκος του, με το πλάτος του και με την ακτίνα του κύκλου, τότε θα έχουμε,

Συνεπώς, το εμβαδό του, 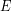, θα είναι,