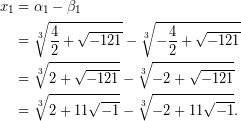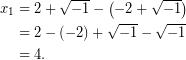“Φανταστικές” … επινοήσεις
Η πρώτη σημαντική πρόοδος στην αλγεβρική επίλυση των τριτοβάθμιων εξισώσεων σημειώνεται στην Ιταλία. Γύρω στο 1515, ο καθηγητής Μαθηματικών Σκιπιόνε νταλ Φέρο (1465-1526), κάτοχος της Έδρας Αριθμητικής και Γεωμετρίας στο Πανεπιστήμιο της Μπολόνια, ανακάλυψε τον τύπο επίλυσης των τριτοβάθμιων εξισώσεων της μορφής,
(1) 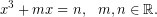
Φυσικά, το γενικό πρόβλημα ανάγεται στην προηγούμενη περίπτωση, μιας και κάθε τριτοβάθμια εξίσωση μπορεί να μετασχηματιστεί όπως παραπάνω με τη μέθοδο “συμπλήρωσης κύβου”.
O νταλ Φέρο κράτησε μυστική την ανακάλυψή του, ωσότου, λίγο πριν τον θάνατό του, την αποκαλύψει στον μαθητή του Αντόνιο Φιόρ.
Έπειτα από δέκα χρόνια, περίπου, ένας προικισμένος μαθηματικός, ο Νικολό Φοντάνα (1499 – 1557), επονομαζόμενος Ταρτάλια, δημοσιοποίησε τον τρόπο επίλυσης τριτοβάθμιων εξισώσεων της μορφής,
![Rendered by QuickLaTeX.com \[ x^{3}+px^{2}=q,\,\,\,\,p,q\in \mathbb{R}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-9ea828ed9696c7442a0e7716d5d80327_l3.png?x32006)
(Ο Φοντάνα έμεινε στην Ιστορία ως “Ταρτάλια”, που σημαίνει τραυλός, εξαιτίας ενός προβλήματος στην άρθρωσή του, έπειτα από ένα σοβαρό παιδικό τραύμα που λίγο έλειψε να του κοστίσει τη ζωή.)
Μετά απ’ αυτήν την εξέλιξη, ο Φιόρ προκάλεσε τον Ταρτάλια σε δημόσιο διαγωνισμό, όπου καθένας τους, εντός διαστήματος 40 ή 50 ημερών, έπρεπε να επιλύσει 30 προβλήματα κυβικών εξισώσεων. Νικητής θα ανακηρυσσόταν εκείνος που θα έλυνε τα περισσότερα. Όμως, οχτώ ημέρες προτού ξεκινήσει ο διαγωνισμός, ο Ταρτάλια είχε καταφέρει να ανανακαλύψει, ανεξάρτητα, τον γενικό τρόπο επίλυσης κυβικών εξισώσεων της μορφής (1). Όλα τα προβλήματα που τέθηκαν από τον Φιόρ ήταν, τροποντινά, αυτής της μορφής, με αποτέλεσμα να λυθούν από τον Ταρτάλια μέσα σε δύο ώρες.
Αργότερα, ο ιδιοφυής μαθηματικός Τζερόλαμο Καρντάνο (1501 – 1576) προσέγγισε τον Ταρτάλια, καταφέρνοντας, με αθέμιτα μέσα, να του αποσπάσει τις ανακαλύψεις του. Στο σπουδαίο έργο του “Μεγάλη τέχνη”, μια πραγματεία στην Άλγεβρα που δημοσιεύτηκε το 1545, παρουσιάζεται ο τύπος με τη βοήθεια του οποίου υπολογίζονται οι ρίζες των κυβικών εξισώσεων.
Ακριβέστερα, ο τύπος με τη βοήθεια του οποίου, αργότερα, θα μπορούσαν να υπολογιστούν οι ρίζες των κυβικών εξισώσεων. Διότι, τουλάχιστον, έτσι όπως αρχικά χρησιμοποιούταν, ήταν δυνατόν να υπολογιστούν μόνο οι ρίζες εξισώσεων όπου οι συντελεστές τους ικανοποιούσαν μια συγκεκριμένη συνθήκη. Ο ίδιος ο Καρντάνο είχε διερευνήσει γενικότερα το πρόβλημα έχοντας επικοινωνήσει, σχετικά, με τον Ταρτάλια. Παρότι έκανε βήματα προς τη σωστή κατεύθυνση, εντούτοις, ελλείψει απτών αποτελεσμάτων, χαρακτήρισε τη μέθοδό του “περισσότερο δεξιοτεχνική, παρά χρήσιμη”. Έτσι, αναγκάστηκε να παραδεχτεί αυτήν την “αδυναμία”, παραπέμποντας, μάλιστα, στις γεωμετρικές τεχνικές του παρελθόντος για μια πληρέστερη αντιμετώπιση του όλου προβλήματος.
Ο Ραφαήλ Μπομπέλι (1526 – 1572), ανίχνευσε με μεγαλύτερη “νηφαλιότητα” και “χωρίς αναστολές” τα “σκοτεινά” σημεία στο έργο του Καρντάνο. Τη χρονιά του θανάτου του, εκδίδεται το βιβλίο του “Άλγεβρα”, στο οποίο ο Μπομπέλι “αποδέχεται” ποσότητες, εκτός του μαθηματικού πλαισίου της εποχής, διευρύνοντας το πεδίο εφαρμογής των τύπων επίλυσης των κυβικών εξισώσεων.
Μέσα από τις διάφορες φάσεις της, με σύγχρονο συμβολισμό και λίγη … “φαντασία”, η ιστορία είχε ως εξής.
Η ταυτότητα,
![Rendered by QuickLaTeX.com \[ \left( \alpha -\beta \right) ^{3}=\alpha ^{3}-3\alpha ^{2}\beta +3\alpha \beta ^{2}-\beta ^{3}, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-cd9a5b9de07bb10c5302cb52db9fccc8_l3.png?x32006)
η οποία γράφεται,
![Rendered by QuickLaTeX.com \[ \left( \alpha -\beta \right) ^{3}+3\alpha\beta\left(\alpha -\beta\right)=\alpha ^{3}-\beta ^{3}, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-7572f57b31e3d5271355625ec4a2e4d0_l3.png?x32006)
υποδεικνύει, για την (1), αναζήτηση λύσης της μορφής,  , με
, με  , όπου,
, όπου,

Διαδοχικά,

οπότε, προκύπτει το σύστημα,

Η δεύτερη εξίσωση του (Σ) είναι δεύτερου βαθμού ως προς 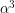 και έχει διακρίνουσα,
και έχει διακρίνουσα,

Έστω,
![Rendered by QuickLaTeX.com \[ D=\left(\dfrac{n}{2}\right)^2+\left(\dfrac{m}{3}\right)^3. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-2ee5b7cfca6598e0b2bb7fdbcfdc7e24_l3.png?x32006)
Περίπτωση Ι)
![Rendered by QuickLaTeX.com \[ D>0. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-9d8217596fbbbdd2196e1c58ea2e9fb8_l3.png?x32006)
Από τη δεύτερη εξίσωση του (Σ), έπεται ότι,
![Rendered by QuickLaTeX.com \[ \alpha^3=\frac{n\pm2\sqrt{D}}{2}=\dfrac{n}{2}\pm\sqrt{D}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-0e960245063a03914da9e3a950e3f7af_l3.png?x32006)
Οπότε, μια δυνατή επιλογή για το  είναι,
είναι,
![Rendered by QuickLaTeX.com \[ \alpha _{1}=\root{3}\of{\frac{n}{2}+\sqrt{D}}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-1e056773afad8d4b123ab67928a02938_l3.png?x32006)
Η αντίστοιχη επιλογή για το 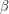 είναι,
είναι,
![Rendered by QuickLaTeX.com \[ \beta _{1}=\root{3}\of{-\frac{n}{2}+\sqrt{D}}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-0ef96ebac1404d3b95c19828870bfec3_l3.png?x32006)
Επομένως, μια ρίζα της εξίσωσης είναι,  , δηλαδή,
, δηλαδή,
(2) 
Με τη βοήθεια αυτής της λύσης, η (1) μετασχηματίζεται ως εξής,
![Rendered by QuickLaTeX.com \[ x^3+mx=n \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-d87d1088431f002d6b97ec2527754c02_l3.png?x32006)
![Rendered by QuickLaTeX.com \[ x^3+3\alpha_{1}\beta_{1}x=\alpha_{1}^{3}-\beta_{1}^{3} \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-347153961955acb351d26bb386cc3852_l3.png?x32006)
![Rendered by QuickLaTeX.com \[ x^{3}+3\alpha _{1}\beta _{1}x-\left( \alpha _{1}^{3}-\beta _{1}^{3}\right) =0 \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-2fa184fe3723c807f27083720c6d10fa_l3.png?x32006)
![Rendered by QuickLaTeX.com \[ x^{3}+3\alpha _{1}\beta _{1}x-\left( \alpha _{1}-\beta _{1}\right) \left( \alpha _{1}^{2}+\alpha _{1}\beta _{1}+\beta _{1}^{2}\right) =0 \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-1a7cbaf1174cbb82593fab946931df0d_l3.png?x32006)
![Rendered by QuickLaTeX.com \[ x^{3}+3\alpha _{1}\beta _{1}x-\left( \alpha _{1}^{2}+\alpha _{1}\beta _{1}+\beta _{1}^{2}\right) x+\left\big( x-\left( \alpha _{1}-\beta _{1}\right)\right\big) \left( \alpha _{1}^{2}+\alpha _{1}\beta _{1}+\beta _{1}^{2}\right) =0 \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-85ac710a62fb7cbbe6ea74997edce327_l3.png?x32006)
![Rendered by QuickLaTeX.com \[ x\big( x-\left( \alpha _{1}-\beta _{1}\right)\big) \left\big( x+\left( \alpha _{1}-\beta _{1}\right)\right\big) +\left\big( x-\left( \alpha _{1}-\beta _{1}\right)\right\big) \left( \alpha _{1}^{2}+\alpha _{1}\beta _{1}+\beta _{1}^{2}\right) =0, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-54b99ada028260372033c7d291d2dd6d_l3.png?x32006)
συνεπώς, γράφεται, τελικά,
(3) 
Το τριώνυμο,
![Rendered by QuickLaTeX.com \[ x^{2}+\left( \alpha _{1}-\beta _{1}\right) x+\alpha _{1}^{2}+\alpha _{1}\beta _{1}+\beta _{1}^{2}, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-dd706268cc46405672ac8e1b40662103_l3.png?x32006)
έχει διακρίνουσα,
![Rendered by QuickLaTeX.com \[ \Delta'=-3(\alpha_{1}+\beta_{1})^{2}, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-990a17ca0b2b162f6c69110bc677dc87_l3.png?x32006)
η οποία έχει αρνητικό πρόσημο διότι,
![Rendered by QuickLaTeX.com \[ \Delta'=0\Leftrightarrow\alpha _{1}=-\beta _{1}\Leftrightarrow D=0. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-a748993f4d49c6a2a7712e3daef02461_l3.png?x32006)
Επομένως, η  είναι η μοναδική πραγματική λύση της (1).
είναι η μοναδική πραγματική λύση της (1).
Έπειτα, κάτι φαινομενικά περιττό:
Θα εκφραστούν τα  με τη βοήθεια της
με τη βοήθεια της  .
.
Για το σκοπό αυτό, παρατηρούμε ότι,

που σημαίνει ότι τα  είναι οι ρίζες της εξίσωσης,
είναι οι ρίζες της εξίσωσης,
![Rendered by QuickLaTeX.com \[ y^2-x_{1}y-\frac{m}{3}=0. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-fdfa433174c3157c6a8294ac5f065140_l3.png?x32006)
Άρα,
(4) 
Παρατήρηση 1 Από τις εκφράσεις (4), έπεται ότι το  είναι ο αντίθετος του συζυγή του
είναι ο αντίθετος του συζυγή του  .
.
Στα επόμενα, θα φανεί η σημασία της τελευταίας παρατήρησης.
Παράδειγμα 1 Για την εξίσωση, 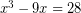 , είναι,
, είναι,  , συνεπώς,
, συνεπώς,
![Rendered by QuickLaTeX.com \[ D =\left(\dfrac{28}{2}\right)^2+\left(\dfrac{-9}{3}\right)^3=196-27=169>0, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-16557efb089df50105332cc5a38abc30_l3.png?x32006)
οπότε, έχει μοναδική πραγματική λύση,
![Rendered by QuickLaTeX.com \[ x_{1}=\alpha_{1}-\beta_{1}=\root{3}\of{\frac{28}{2}+\sqrt{169}}-\root{3}\of{-\frac{28}{2}+\sqrt{169}}=\root{3}\of{27}-\root{3}\of{-1}=3-(-1)=4. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-2d77718d10d0fef272103ec727daa0a5_l3.png?x32006)
Από την άλλη μεριά, βάσει της λύσης  , χρησιμοποιώντας τους τύπους (4),
, χρησιμοποιώντας τους τύπους (4),

Οι παραπάνω εναλλακτικές εκφράσεις για τα  , στο προηγούμενο παράδειγμα, δεν προσθέτουν, φυσικά, τίποτα καινούριο στην επίλυση της συγκεκριμένης εξίσωσης. Ωστόσο, με την ένταξή τους, μπορεί κανείς να είναι περισσότερο υποψιασμένος για τα όσα ακολουθούν.
, στο προηγούμενο παράδειγμα, δεν προσθέτουν, φυσικά, τίποτα καινούριο στην επίλυση της συγκεκριμένης εξίσωσης. Ωστόσο, με την ένταξή τους, μπορεί κανείς να είναι περισσότερο υποψιασμένος για τα όσα ακολουθούν.
Περίπτωση ΙΙ)
![Rendered by QuickLaTeX.com \[ D\leq 0. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-cd97a5d2ef6430c1a1b21d659a887166_l3.png?x32006)
Για την ώρα, η ειδική περίπτωση της εξίσωσης,
(5) 
για την οποία είναι,  , οπότε,
, οπότε,
![Rendered by QuickLaTeX.com \[ D=\left(\dfrac{4}{2}\right)^2+\left(\dfrac{-15}{3}\right)^3=4-125=-121<0. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-33667044400f605255bf379c9e5a9c76_l3.png?x32006)
Σύμφωνα με την ανάλυση που έγινε στην Περίπτωση Ι, γίνεται φανερό ότι δεν υπάρχει λύση  της μορφής
της μορφής  με
με  , τέτοια, ώστε,
, τέτοια, ώστε,

Από την άλλη μεριά, η εξίσωση έχει προφανή λύση τη 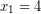 . Έτσι, παραγοντοποιώντας, γράφεται, ισοδύναμα,
. Έτσι, παραγοντοποιώντας, γράφεται, ισοδύναμα,
(6) 
Συνεπώς, οι ρίζες της είναι,
![Rendered by QuickLaTeX.com \[x_{1}=4,\,\,\,\,x_{2}=-2+\sqrt{3},\,\,\,\,x_{3}=-2-\sqrt{3}.\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-4bee9aa4036632a58db15f224c38eefc_l3.png?x32006)
Επομένως, η (6) έχει τρεις πραγματικές ρίζες.
Επιπλέον, σ’ αυτήν την περίπτωση, οι τύποι (4) δεν ισχύουν, ωστόσο, αν τα “εξαγόμενά τους”,

για τη λύση  , μπορούσαν να ενσωματωθούν στην “οικογένεια” των αριθμών, εμπλουτίζοντάς την, με τέτοιο τρόπο, έτσι, ώστε, να “υπακούν” στους “νόμους” των πράξεων, τότε η (6) θα ήταν, πάλι, της μορφής (3). Πράγματι,
, μπορούσαν να ενσωματωθούν στην “οικογένεια” των αριθμών, εμπλουτίζοντάς την, με τέτοιο τρόπο, έτσι, ώστε, να “υπακούν” στους “νόμους” των πράξεων, τότε η (6) θα ήταν, πάλι, της μορφής (3). Πράγματι,

Βέβαια, έστω και μ’ αυτήν την υπέρβαση, παραμένει ανοικτό το πρόβλημα εύρεσης των  μιας και υπολογίστηκαν με τη βοήθεια της λύσης
μιας και υπολογίστηκαν με τη βοήθεια της λύσης  της (5). Φυσικά, δε μπορεί να θεωρείται γνωστή, εκ των προτέρων, μια λύση για την τριτοβάθμια εξίσωση που επιλύεται.
της (5). Φυσικά, δε μπορεί να θεωρείται γνωστή, εκ των προτέρων, μια λύση για την τριτοβάθμια εξίσωση που επιλύεται.
Αψηφώντας, για δεύτερη φορά, βασική ιδιότητα της διάταξης των πραγματικών αριθμών, επιστρατεύεται ο τύπος (2), με την προσδοκία άμεσου υπολογισμού ρίζας για την εξίσωση (5). Έτσι,
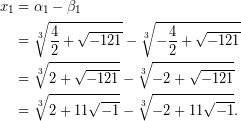
Τώρα, εφαρμόζοντας τις ιδιότητες των πράξεων, όπως στην περίπτωση των πραγματικών αριθμών, έπεται ότι,

που σημαίνει ότι,
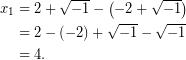
Ίσως ο υπολογισμός της  να είναι, πάλι, έμμεσος, όμως, αναδεικνύεται, ξανά, το ενδεχόμενο αξιοποίησης αυτών των “φανταστικών” εκφράσεων.
να είναι, πάλι, έμμεσος, όμως, αναδεικνύεται, ξανά, το ενδεχόμενο αξιοποίησης αυτών των “φανταστικών” εκφράσεων.
Για άλλη μια φορά οι Μαθηματικοί βρέθηκαν μπροστά σ’ ένα δίλλημα. Να αποδεχτούν, κατ’ αρχήν, αυτές τις εκφράσεις, από τη στιγμή που διαφαινόταν η συνεισφορά τους στο γενικό πρόβλημα της επίλυσης της τριτοβάθμιας εξίσωσης, ή να τις απορρίψουν διότι, μέχρι τότε, στερούνταν νοήματος και, στη συνέχεια, να στραφούν σε άλλες στρατηγικές για την επίλυσή του.
Επέλεξαν αυτό που ίσως, αρχικά, έμοιαζε αδιανόητο. Η πρόκληση ήταν σίγουρα σπουδαία μα το εγχείρημα καθόλου εύκολο. Έπρεπε να θεμελιωθεί ένα υπερσύνολο των πραγματικών αριθμών το οποίο να έχει ένα στοιχείο, έστω  , επιφορτισμένο να αναλάβει το ρόλο που είχε η έκφραση
, επιφορτισμένο να αναλάβει το ρόλο που είχε η έκφραση  παραπάνω. Επιπλέον, να έχει τις ίδιες πράξεις με το
παραπάνω. Επιπλέον, να έχει τις ίδιες πράξεις με το  και τις ίδιες ιδιότητες των πράξεων. Τα στοιχεία του, ως αποτέλεσμα των “προσμίξεών” του με τους πραγματικούς αριθμούς, έπρεπε να έχουν τη μορφή,
και τις ίδιες ιδιότητες των πράξεων. Τα στοιχεία του, ως αποτέλεσμα των “προσμίξεών” του με τους πραγματικούς αριθμούς, έπρεπε να έχουν τη μορφή,
![Rendered by QuickLaTeX.com \[ \alpha+\beta\cdot i,\,\,\,\,\alpha,\beta\in \mathbb{R}, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-61de561cf366903e37dfd137e9285270_l3.png?x32006)
όπου  .
.
Άραγε, οι αριθμοί, εκτός από το να «αριθμούν», θα μπορούσαν, απλά, να υπόκεινται στις ιδιότητες που απορρέουν από τις αριθμητικές πράξεις;
Όταν ο αρχικός σκεπτικισμός ξεπεράστηκε, δίνοντας τη θέση του σε μια κριτική αναθεώρηση των ορισμών των διάφορων συνόλων των αριθμών, άρχισε να συγκροτείται το σύνολο  των μιγαδικών. Προτεραιότητα δεν αποτέλεσε τόσο η φυσική ερμηνεία των στοιχείων του, όπως αυτά περιγράφηκαν παραπάνω, όσο η συνεπής μεταφορά, κατά τη δόμηση του νέου συνόλου, των πράξεων των πραγματικών και η ταυτόχρονη απελευθέρωση από τα δεσμά που επέβαλλε η διάταξη.
των μιγαδικών. Προτεραιότητα δεν αποτέλεσε τόσο η φυσική ερμηνεία των στοιχείων του, όπως αυτά περιγράφηκαν παραπάνω, όσο η συνεπής μεταφορά, κατά τη δόμηση του νέου συνόλου, των πράξεων των πραγματικών και η ταυτόχρονη απελευθέρωση από τα δεσμά που επέβαλλε η διάταξη.
Αναφορές
- Eves H., Great moments in Mathematics Before 1650, Mathematical Association Of America, 1983.
- Henderson D.W., Geometric Solutions of quadratic and Cubic Equations, Department of Mathematics, Cornell University.
- O’Connor J. J. and Robertson E. F., Quadratic, Cubic and quartic equations, School of Mathematics and Statistics University of St Andrews, Scotland , 1996.
![]()
![]()
![]() των πραγματικών στο σύνολο
των πραγματικών στο σύνολο ![]() των μιγαδικών.
των μιγαδικών.![]() , μπορεί να αναζητηθεί, για την (1), λύση της μορφής,
, μπορεί να αναζητηθεί, για την (1), λύση της μορφής, ![]() , όπου,
, όπου, ![]() , τέτοια, ώστε,
, τέτοια, ώστε,![]()

![]() , όπως η έννοια του συζυγούς, του μέτρου και της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και βασικά συμπεράσματα που τις διέπουν, με κυριότερο το Θεώρημα De Moivre.
, όπως η έννοια του συζυγούς, του μέτρου και της τριγωνομετρικής μορφής ενός μιγαδικού αριθμού, καθώς και βασικά συμπεράσματα που τις διέπουν, με κυριότερο το Θεώρημα De Moivre.![]() , μια εξίσωση της μορφής,
, μια εξίσωση της μορφής, ![]() με
με ![]() , ισοδύναμα, γράφεται,
, ισοδύναμα, γράφεται,![]()
![]() και
και ![]() .
.![]()
![]() , μπορεί να προκύψει από την ισότητα,
, μπορεί να προκύψει από την ισότητα,![]()
![]() πρέπει να πληροί,
πρέπει να πληροί,![]()
![]()
![]() , ο αντίθετος του συζυγή του
, ο αντίθετος του συζυγή του ![]() ,
,![]()
![]()
![]() .
.![]()
![]()
![]() τέτοια, ώστε,
τέτοια, ώστε,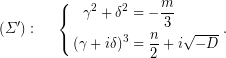
![]() , προφανώς
, προφανώς ![]() .
.![Rendered by QuickLaTeX.com \[ \Bigg(\dfrac{\gamma}{\sqrt{-\dfrac{m}{3}}}\Bigg)^2+\Bigg(\dfrac{\delta}{\sqrt{-\dfrac{m}{3}}}\Bigg)^2=1. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-d4860922ea5809448b8c5e333da88d66_l3.png?x32006)
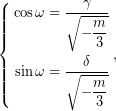

![]() συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)
συμβολίζονται το συνημίτονο και το ημίτονο αντίστοιχα.)![]()
![Rendered by QuickLaTeX.com \[ \left(\cos\omega+i\sin\omega\right)^3=\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}+i\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-6f7a69efa6e8d566f77108122faf0d88_l3.png?x32006)

![Rendered by QuickLaTeX.com \[ \cos(3\omega)+i\sin(3\omega)=\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}+i\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-a8e7dc3d2bfaf1750f93e876e3616a67_l3.png?x32006)
![]() τέτοια, ώστε,
τέτοια, ώστε,
![Rendered by QuickLaTeX.com \[ \Bigg(\dfrac{\dfrac{n}{2}}{\sqrt{-\dfrac{m}{3}}^{3}}\Bigg)^2+\Bigg(\dfrac{\sqrt{-D}}{\sqrt{-\dfrac{m}{3}}^{3}}\Bigg)^2=\dfrac{\Big(\dfrac{n}{2}\Big)^2-D}{-\Big(\dfrac{m}{3}\Big)^3}=1, \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-60cb133984cd1646b29f34c0b0345ad2_l3.png?x32006)
![]() είναι μια τέτοια λύση, τότε,
είναι μια τέτοια λύση, τότε, ![]() είναι λύση του (Σ΄), όπου,
είναι λύση του (Σ΄), όπου,
![]() είναι λύση του (Σ), όπου,
είναι λύση του (Σ), όπου,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
έχει τρεις πραγματικές λύσεις που δίνονται από τους τύπους,
![]() , έχουμε,
, έχουμε, ![]() , συνεπώς,
, συνεπώς,![]()
![]() , τέτοιο, ώστε,
, τέτοιο, ώστε,
![]() το
το ![]() .
.