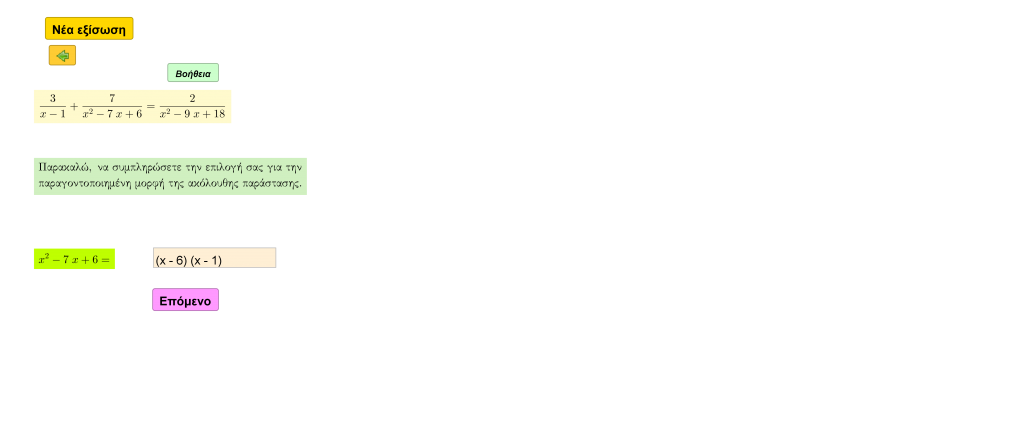Όταν ο άγνωστος μιας εξίσωσης εμφανίζεται στον παρονομαστή ενός κλάσματος, τότε, η εξίσωση ονομάζεται κλασματική.
Στην ειδικότερη περίπτωση, όπου οι όροι της εξίσωσης έχουν ή μπορούν να πάρουν τη μορφή κλασμάτων, όπου τόσο ο αριθμητής όσο και ο παρονομαστής είναι πολυώνυμα, η εξίσωση λέγεται ρητή.
Κατά την επίλυση μιας ρητής εξίσωσης, αρχικά, καλό είναι να περιοριστεί το πεδίο αναζήτησης των λύσεών της, εξαιρώντας τις τιμές της μεταβλητής που μηδενίζουν τους εμφανιζόμενους παρονομαστές. Γι’ αυτό αποδεικνύεται, ιδιαίτερα, χρήσιμο οι παρονομαστές να έχουν προηγουμένως παραγοντοποιηθεί. Η παραγοντοποίηση, άλλωστε, συμβάλλει στον υπολογισμό του ΕΚΠ των παρονομαστών, βήμα σημαντικό κατά τη μετέπειτα απαλοιφή τους. Πολλαπλασιάζοντας όλους τους όρους μιας κλασματικής εξίσωσης με το ΕΚΠ των παρονομαστών της, μετά την εκτέλεση των απλοποιήσεων που προκύπτουν, η αρχική εξίσωση μετασχηματίζεται σε πολυωνυμική εξίσωση όπου, στο πλαίσιο της Γ΄ Γυμνασίου, συνήθως, πρόκειται για μια εξίσωση πρώτου ή δεύτερου βαθμού.
Γενικά, είναι διαπιστωμένο ότι η ενότητα αυτή εμφανίζει σημαντικές δυσκολίες, κατά τη διδακτική προσέγγιση, αφού προϋποθέτει πλήρη κατανόηση για μια πληθώρα προ απαιτούμενων γνώσεων όπως ταυτότητες, παραγοντοποίηση, εύρεση ΕΚΠ, απλοποίηση, επιμεριστική ιδιότητα, αναγωγή όμοιων όρων, επίλυση εξισώσεων πρώτου και δεύτερου βαθμού.
Η διαδραστική εφαρμογή που ακολουθεί, πραγματεύεται τα παραπάνω θέματα για ποικίλες ρητές εξισώσεις παρέχοντας τη δυνατότητα ελέγχου των απαντήσεων του χρήστη αλλά και κάποιων κατευθυντήριων γραμμών μέσα από κατάλληλες υποδείξεις.
και ένα τετράγωνο πλευράς 
, τα οποία έχουν τοποθετηθεί στο επίπεδο, κατά τέτοιον τρόπο, ώστε να έχουν μοναδικό κοινό σημείο και κάθε πλευρά του πρώτου να είναι παράλληλη προς μια πλευρά του δεύτερου. «Συμπληρώνουμε» το σχήμα, χρησιμοποιώντας κατάλληλα ορθογώνια, έτσι, ώστε, να σχηματιστεί το τετράγωνο πλευράς 
της Εικόνας 2.
,
