Ο π-e-λάτης έχει πάντα δίκιο!

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 30-03-2016

Το 1683, ο μεγάλος Ελβετός Μαθηματικός Jacob Bernoulli (1655 – 1705), στην προσπάθεια εύρεσης της βέλτιστης λύσης ενός προβλήματος ανατοκισμού, ήρθε αντιμέτωπος με τον υπολογισμό της παράστασης,

    \[$\left ( \displaystyle\frac{\nu+1}{\nu} \right )^\nu$\]

για “μεγάλες” τιμές του \nu,

δηλαδή, τροποντινά, με τον υπολογισμό του ορίου,

    \[$\displaystyle\lim_{\nu \rightarrow +\infty}\left ( \frac{\nu+1}{\nu} \right )^\nu$.\]

Σήμερα, η (άρρητη) τιμή του παραπάνω ορίου είναι γνωστή ως “αριθμός του Euler”, προς τιμήν, ενός άλλου σπουδαίου Ελβετού Μαθηματικού, του Euler (1707 – 1783). Συμβολίζεται διεθνώς με το e, γράμμα που ο ίδιος ο Euler υϊοθέτησε για να τον παραστήσει.

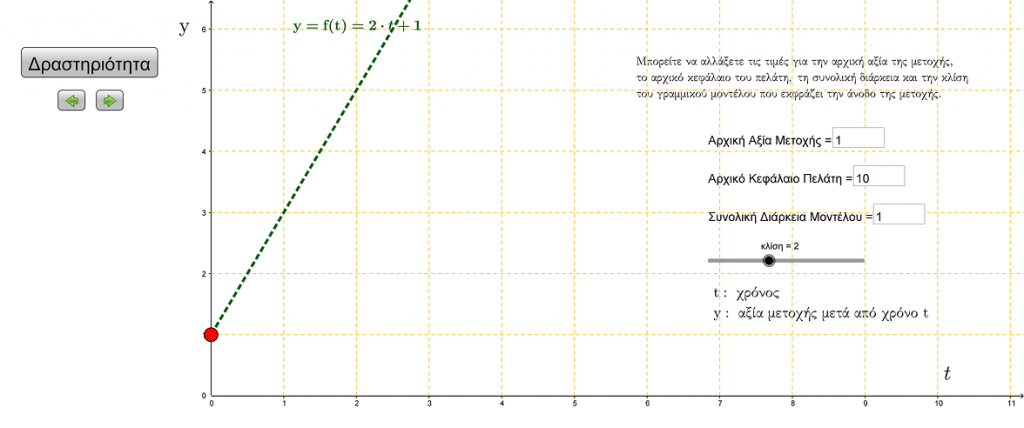
Στην ακόλουθη διαδραστική εφαρμογή, πιθανώς, σ’ ένα πρόβλημα, παρόμοιο μ’ αυτό που οδήγησε στην ανακάλυψη του e, καλείστε να βοηθήσετε έναν χρηματιστή να διαφυλάξει τα συμφέροντα του πελάτη του. Ίσως να χρειαστεί να υπολογίσετε την προσεγγιστική τιμή του αριθμού του Euler, όπως και διάφορες δυνάμεις του, απαντώντας, έτσι, την αντίστοιχη εκθετική συνάρτηση.

Funds

Διαβάστε περισσότερα

Σκια … γραφώντας τη λογαριθμική συνάρτηση

0

Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 30-05-2015

Μια συγκεκριμένη μέθοδος “τετραγωνισμού” της υπερβολής,

    \[y=\frac{\alpha}{x}, \,\,\,\, x \neq 0\]

δηλαδή, προσέγγισης από ορθογώνια του εμβαδού του χωρίου που περικλείεται από το γράφημά της, τον οριζόντιο άξονα, και δύο κατάλληλες κατακόρυφες ευθείες, οδηγεί με φυσικό τρόπο στην έννοια της λογαριθμικής συνάρτησης με βάση τον αριθμό e.

Η μέθοδος αυτή, ίσως, να πρέπει να αποδοθεί στον Βέλγο Ιησουίτη Grégoire de Saint – Vincent (1584 – 1667), γνωστό με το προσωνύμιο του “κυκλοτετραγωνιστή”, ο οποίος σίγουρα στηρίχθηκε σε προγενέστερες εργασίες του Γάλλου μαθηματικού και δικηγόρου Pierre de Fermat (1601 – 1665) για το αντίστοιχο πρόβλημα τετραγωνισμού καμπυλών που περιγράφονται από τον γενικό τύπο,

    \[ y=x^n. \]

(Γενικευμένες Παραβολές.)

Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής μπορείτε να δοκιμάσετε να “τετραγωνίσετε” την υπερβολή, σκια … γραφώντας την αντίστοιχη λογαριθμική συνάρτηση.

logarithmic_function

Αναφορές

  1. Maor Eli, e: Η Ιστορία ενός αριθμού, Πανεπιστήμιο Loyola, Σικάγο, Εκδόσεις κάτοπτρο

Διαβάστε περισσότερα

Αλλαγή μεγέθους γραμματοσειράς
Αντίθεση
Accessibility by WAH