Ασκήσεις – Προβλήματα
ΠΗΓΗ: Ylikonet.gr
Πατείστε την εικόνα
Κατηγορία: 3.05 Νόμοι Αερίων – Κινητική Θεωρία
Τα αέρια της Β συνεργάζονται με τα ρευστά της Γ;
Στον πυθμένα των λιμνών συχνά παρατηρείται σχηματισμός φυσαλίδων αερίου CΗ4. Έχοντας πυκνότητα μικρότερη από την πυκνότητα του νερού, ανέρχονται προς την επιφάνεια της λίμνης.
- Ο όγκος αυτών των φυσαλίδων αυξάνεται κατά την άνοδο. Μπορείτε να εξηγήσετε το φαινόμενο;
- Ένας δύτης – ερευνητής πήρε κάποιες μετρήσεις. Θερμοκρασία στον πυθμένα θ1 = 170C, θερμοκρασία στην επιφάνεια θ2 = 270C και ατμοσφαιρική πίεση p2 = p0 = 1∙105N/m2. Υπολόγισε επίσης ότι ο όγκος μιας φυσαλίδας τετραπλασιάζεται μέχρι την επιφάνεια της λίμνης. Βρήκε έτσι την πίεση κοντά στον πυθμένα. Πόσο;
- Θεωρώντας την πυκνότητα του νερού ρ = 103kg/m3, πόσο λέτε ότι κατάφερε να βρει το βάθος της θάλασσας;
- Αν είχε θεωρήσει τη μεταβολή ισόθερμη πόσο % θα ήταν το σφάλμα του;
Θεωρείστε ότι η φυσαλίδα ανεβαίνει αργά, ώστε η πίεση και η θερμοκρασία στο εσωτερικό της προλαβαίνει να εξισώνεται με την πίεση του νερού εξωτερικά. Επίσης g = 10m/s2.
Ιδανικό αέριο και διάγραμμα P – T
Ιδανικό αέριο υφίσταται τη μεταβολή του διπλανού σχήματος.
Στην κατάσταση Γ δίνεται ότι VΓ = VA / 3.
α) Ποιο είναι το είδος της κάθε μεταβολής;
β) Ποια είναι η εξίσωση P = f(T) της μεταβολής ΒΔ;
γ) Ποια είναι η πίεση του αερίου στην κατάσταση Γ;
Μια ισόθερμη και ένα ελατήριο
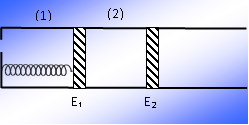Το οριζόντιο κυλινδρικό δοχείο που φαίνεται στο σχήμα, έχει στο εσωτερικό του δύο έμβολα Ε1 και Ε2, τα οποία ισορροπούν ακίνητα. Έτσι το δοχείο χωρίζεται σε δύο μέρη 1 και 2, που περιέχουν αέρα, ίσου όγκου V = 2.10-3m3. Στο έμβολο Ε1 βρίσκεται στερεωμένο το ένα άκρο οριζόντιου ιδανικού ελατηρίου, που έχει το άλλο άκρο του δεμένο στο αριστερό ακλόνητο τοίχωμα – βάση του δοχείου. Το τοίχωμα αυτό έχει μικρή τρύπα, ώστε ο χώρος 1, που βρίσκεται το ελατήριο να επικοινωνεί με την ατμόσφαιρα.
i) Αποδείξτε ότι το ελατήριο δεν είναι παραμορφωμένο και υπολογίστε το φυσικό του μήκος.
ii) Σπρώχνουμε αργά το έμβολο Ε2 προς τα αριστερά και παρατηρούμε ότι και το έμβολο Ε1 μετακινείται προς τα αριστερά.
α) Γιατί μετακινείται το έμβολο Ε1;
β) Ποιος θα είναι ο τελικός όγκος του αέρα ανάμεσα στα δύο έμβολα;
γ) Ποια θα είναι η τελική πίεση του αέρα ανάμεσα στα δύο έμβολα;
Δίνονται: η σταθερά του ελατηρίου k = 1000Ν/m, το εμβαδόν της κυκλικής βάσης του δοχείου A = 100cm2 και η ατμοσφαιρική πίεση patm = 105N/m2.
ΤΥΠΟΛΟΓΙΟ ΘΕΡΜΟΔΥΝΑΜΙΚΗΣ ΚΑΙ ΜΕΘΟΔΟΛΟΓΙΑ
.gif)
Μελετήστε ένα χρήσιμο ΤΥΠΟΛΟΓΙΟ και διαβάστε μια ΜΕΘΟΔΟΛΟΓΙΑ, από τον Βαγγέλη Μαρούση.
Νόμοι Αερίων – Κινητική θεωρία – Ασκήσεις
Από τον Γιώργο Παπαδημητρίου
δείτε ΕΔΩ μια συλλογή ασκήσεων.
Πειραματική μελέτη των νόμων για τα αέρια
Δείτε ένα Φύλλο Εργασίας του Διονύση Μάργαρη.
