Ο Γαλιλαίος αποτελεί μία από τις πιο εμβληματικές φυσιογνωμίες στην ιστορία της επιστήμης. Το Ίδρυμα Ευγενίδου αποδίδει τον δικό του φόρο τιμής στον σπουδαίο μαθηματικό και αστρονόμο με τη δημιουργία του ντοκιμαντέρ «Γαλιλαίος: Η Μάχη στην Αυγή της Σύγχρονης Επιστήμης». Συνέχεια του άρθρου ‘«Γαλιλαίος: Η Μάχη στην Αυγή της Σύγχρονης Επιστήμης». Εκπαιδευτικό υλικό’ »
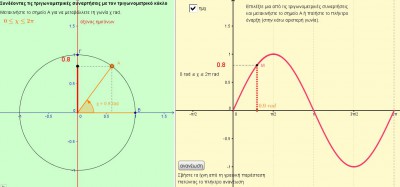
Συνδέοντας τις τριγωνομετρικές συναρτήσεις με τον τριγωνομετρικό κύκλο
Διαδραστική μαθησιακή δραστηριότητα στην τριγωνομετρία της Β΄ Λυκείου.
Μετάβαση στο φύλλο εργασίας του μαθητή
Επειδή η συνάρτηση f(x) = ημx είναι περιοδική με περίοδο 2π, αρκεί να τη μελετήσουμε σε ένα διάστημα πλάτους 2π, π.χ. το [0, 2π]. Το ίδιο ισχύει για τη συνάρτηση g(x) = συνx. Οι συναρτήσεις h(x) = εφx και k(x) = σφx είναι περιοδικές με περίοδο π.
Το ημx είναι η τεταγμένη του σημείου Α στο οποίο η τελική πλευρά της γωνίας x rad τέμνει τον τριγωνομετρικό κύκλο. Επομένως αρκεί να εξετάσουμε πώς μεταβάλλεται η τεταγμένη του Α, όταν αυτό περιφέρεται στον τριγωνομετρικό κύκλο κατά τη θετική φορά, ξεκινώντας από το Β. Αντίστοιχα μπορούμε να σκεφτούμε και για τους άλλους τριγωνομετρικούς αριθμούς. Συνέχεια του άρθρου ‘Συνδέοντας τις τριγωνομετρικές συναρτήσεις με τον τριγωνομετρικό κύκλο’ »
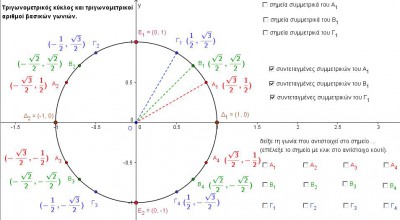
Τριγωνομετρικοί αριθμοί βασικών γωνιών
Διαδραστική εφαρμογή στην τριγωνομετρία της Β΄ Λυκείου
Μετάβαση στο φύλλο εργασίας του μαθητή
Οι συντεταγμένες των σημείων Α1, Β1 και Γ1, που βρίσκονται πάνω στον τριγωνομετρικό κύκλο, δηλώνουν το ημίτονο και το συνημίτονο των γωνιών Δ1ΟΑ1, Δ1ΟΒ1 και Δ1ΟΓ1 αντίστοιχα. Με τη βοήθεια αυτών θα βρούμε τους τριγωνομετρικούς αριθμούς και άλλων γωνιών. Συνέχεια του άρθρου ‘Τριγωνομετρικοί αριθμοί βασικών γωνιών’ »
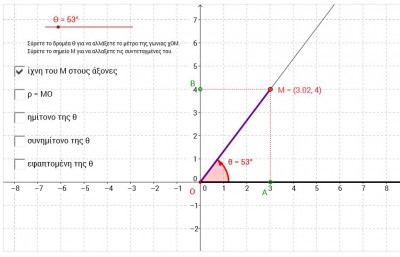
Τριγωνομετρικός κύκλος
Διαδραστική εφαρμογή στην τριγωνομετρία της Β΄ Λυκείου
Μετάβαση στο φύλλο εργασίας του μαθητή
Ο βασικός στόχος της δραστηριότητας είναι να δοθεί στους οι μαθητές η δυνατότητα να οπτικοποιήσουν τους τριγωνομετρικούς αριθμούς οποιασδήποτε γωνίας και να συνδέσουν διαισθητικά, τις τιμές τους και τις μεταβολές τους με τις τιμές και τις μεταβολές της γωνίας Συνέχεια του άρθρου ‘Τριγωνομετρικός κύκλος’ »
Τριγωνομετρικοί αριθμοί οποιασδήποτε γωνίας
Διαδραστική μαθησιακή δραστηριότητα στην τριγωνομετρία της Γ΄ Γυμνασίου
Διδακτικοί στόχοι της δραστηριότητας.
Με τη βοήθεια της μικροεφαρμογής και με κατάλληλες ερωτήσεις του διδάσκοντα, οι μαθητές:
θα θυμηθούν πως ορίζονται οι τριγωνομετρικοί αριθμοί μιας οξείας γωνίας ορθογωνίου τριγώνου.
Θα μάθουν πως ορίζονται (και για ποιο λόγο ορίζονται έτσι) οι τριγωνομετρικοί αριθμοί μιας οποιασδήποτε γωνίας από 00 έως 3600 με τη βοήθεια ενός ορθογωνίου συστήματος αξόνων. Συνέχεια του άρθρου ‘Τριγωνομετρικοί αριθμοί οποιασδήποτε γωνίας’ »
Αξονική & κεντρική συμμετρία
Διαδραστική εφαρμογή στη συμμετρία.
Οι μαθητές πειραματίζονται με την αξονική και την κεντρική συμμετρία με σκοπό να ανακαλύψουν τις ιδιότητες τους, τις ομοιότητες και τις διαφορές τους.
Γρίφοι & σπαζοκεφαλιές για μαθητές (β΄ μέρος)
Σ’ αυτό το θέμα θα δημοσιεύονται γρίφοι και σπαζοκεφαλιές που έχουν ως στόχο να σας προβληματίσουν αλλά και να σας διασκεδάσουν. Προσφέρουν τη δυνατότητα να ξεφύγετε από τη ρουτίνα της καθημερινότητας και ταυτόχρονα να εξασκήσετε το μυαλό σας και να καλλιεργήσετε τη σκέψη, τη λογική, τη φαντασία και την παρατηρητικότητα σας. Συνέχεια του άρθρου ‘Γρίφοι & σπαζοκεφαλιές για μαθητές (β΄ μέρος)’ »
Πρόσφατες ψυχολογικές μελέτες που πρέπει να γνωρίζουν οι γονείς
Ένας από τους πολλούς λόγους που η ανατροφή των παιδιών είναι τόσο δύσκολη, είναι και το ότι οι γονείς συχνά γίνονται δέκτες αντικρουόμενων συμβουλών. Οι περισσότερες από τις οποίες στερούνται επιστημονικού υπόβαθρου, ενώ αρκετές είναι αποδεδειγμένα λανθασμένες. Οι παρακάτω δέκα νέες ψυχολογικές μελέτες , θα βοηθήσουν να λυθούν κάποιες από τις χιλιάδες απορίες που έχει κάθε γονιός. Συνέχεια του άρθρου ‘Πρόσφατες ψυχολογικές μελέτες που πρέπει να γνωρίζουν οι γονείς’ »
Η Γεωμετρία των Fractals και ο μαθηματικός Benoît Mandelbrot που την επινόησε
Ακόμα κι αν γνωρίζετε ελάχιστα μαθηματικά, τα Fractals, μάλλον δεν σας είναι άγνωστα. Έχετε ακούσει ότι πρόκειται για γεωμετρικά σχήματα που επαναλαμβάνονται αυτούσια σε άπειρο βαθμό μεγέθυνσης και ότι οποιοδήποτε τμήμα τους κι αν μεγεθυνθεί εξακολουθεί να απεικονίζει μια μερική ή ολική επανάληψη του αρχικού σχεδίου. Συνέχεια του άρθρου ‘Η Γεωμετρία των Fractals και ο μαθηματικός Benoît Mandelbrot που την επινόησε’ »
Σχολείο ανοιχτό προς όλες τις απόψεις
Το σημερινό σχολείο είναι ανοιχτό προς όλες τις απόψεις, δήλωσε εγγράφως στη Βουλή ο υφυπουργός Παιδείας Σ. Κεδίκογλου, επικαλούμενος το 7198/5-11-13 έγγραφο του ΙΕΠ, και υπογράμμισε τα εξής:
Α. Όλες οι απόψεις κρίνονται και συζητούνται στο πλαίσιο του μαθήματος.
Β. Μια άποψη, άλλωστε ακόμα και αν αποσιωπηθεί εντός του σχολείου, διακινείται στις μέρες μας πολύ εύκολα. Συνέχεια του άρθρου ‘Σχολείο ανοιχτό προς όλες τις απόψεις’ »