Οι γρίφοι και οι σπαζοκεφαλιές σας δίνουν τη δυνατότητα να διασκεδάσετε, να ψυχαγωγηθείτε και ταυτόχρονα  να εξασκήσετε το μυαλό σας  και να καλλιεργήσετε τη σκέψη, τη λογική, τη φαντασία και την παρατηρητικότητα σας. Έτσι, ακονίζετε το μυαλό σας και αποκτάτε σταδιακά  την ικανότητα να λύνετε προβλήματα με μεγαλύτερη ευκολία.

Σε κάθε γρίφο θα αναγράφεται ο βαθμός δυσκολίας του, καθώς και οι τάξεις γυμνασίου και λυκείου στις οποίες απευθύνεται. Οι βαθμοί δυσκολίας είναι: 1 για το εύκολο, 2 για το μέτριο και 3 για το σύνθετο.

 

1. «Η έξυπνη μέτρηση». Βαθμός δυσκολίας 1.   Τάξεις: όλες.

Έχει κάποιος κρασί και θέλει να δώσει στο φίλο του 1 λίτρο. Πώς μπορεί να το κάνει αυτό χρησιμοποιώντας μόνο ένα δοχείο των 5 λίτρων και ένα των 3 λίτρων;  (στα δοχεία δεν μπορούμε να χρησιμοποιήσουμε κλίμακα)

ΛΥΣΗ 1ου:
Πρώτα θα γεμίσει το δοχείο των 3 λίτρων. Μετά θα αδειάσει τα 3 λίτρα στο δοχείο των 5 λίτρων. Στη συνέχεια θα γεμίσει και πάλι το δοχείο των 3 λίτρων και θα αδειάσει στο δοχείο των 5 λίτρων τόσο κρασί, ώστε να το γεμίσει (χωρούσε 2 λίτρα ακόμη για να γεμίσει). Έτσι θα μείνει στο δοχείο των 3 λίτρων ακριβώς 1 λίτρο.

Οι πέντε πρώτοι μαθητές/τριες που απάντησαν σωστά ήταν:
1. Φιλιώ Πολίτη, Α’ γυμνασίου
2. Κλειώ Σαϊτάκη, Α’ γυμνασίου
3. Λευτέρης Φουστέρης, Α’ γυμνασίου
4. Άρης Αρβανιτάκης, Γ’ γυμνασίου
5. Άρης Κίγκος, Γ’ γυμνασίου

2. «Το τούβλο». Βαθμός δυσκολίας 2. Τάξεις: όλες.

Ένα τούβλο ζυγίζει ένα κιλό και μισό τούβλο. Πόσα κιλά ζυγίζουν τα δύο τούβλα;

ΛΥΣΗ 2ου:
Tα δύο τούβλα ζυγίζουν 4 κιλά. Επειδή ένα τούβλο ζυγίζει ένα κιλό και μισό τούβλο, άρα αν αφαιρέσουμε μισό τούβλο από το κάθε δίσκο της ζυγαριάς, θα βρούμε πως το μισό τούβλο ζυγίζει ένα κιλό οπότε τα δύο τούβλα ζυγίζουν 4 κιλά.

Οι πέντε πρώτοι μαθητές/τριες που απάντησαν σωστά ήταν:
1. ΕλένηΤασιά, Α’ γυμνασίου
2. Βάσω Σώμου, Α’ γυμνασίου
3. Λευτέρης Φουστέρης, Α’ γυμνασίου
4. Άρης Κίγκος, Γ’ γυμνασίου
5. Άρης Αρβανιτάκης, Γ’ γυμνασίου

3. «Το νούφαρο».  Βαθμός δυσκολίας 1.  Τάξεις: όλες.

Ένα νούφαρο κάθε μέρα διπλασιάζεται σε μέγεθος και την 100η μέρα κάλυψε ολόκληρη την επιφάνεια μιας λίμνης. Να βρείτε ποια μέρα είχε καλύψει τη μισή λίμνη.

Λύση 3ου: Αν το νούφαρο διπλασιάζεται κάθε μέρα, θα καλύψει το βάλτο την παραμονή της μέρας που τον γεμίζει ολόκληρο. Άρα καλύπτει το μισό βάλτο την 99η μέρα.

Οι  μαθητές/τριες που απάντησαν σωστά ήταν:
1. Αντώνης Ρούντας,  Α’ γυμνασίου
2.  Άρης Αρβανιτάκης,  Γ’ γυμνασίου
3.  Λευτέρης Φουστέρης,  Α’ γυμνασίου

4. «Το ασανσέρ». Βαθμός δυσκολίας 1.   Τάξεις: όλες.

Κάθε πρωί, ένας μαθητής που μένει στο 8^ο όροφο μιας πολυκατοικίας, κατεβαίνει με το ασανσέρ τους 8 ορόφους και πηγαίνει στο σχολείο. Κάθε μεσημέρι, όταν επιστρέφει από το σχολείο, ανεβαίνει με  το ασανσέρ μέχρι τον 6^ο όροφο και συνεχίζει με τις σκάλες. Γιατί συμβαίνει αυτό;

Λύση 4ου : Αυτό συμβαίνει γιατί ο μαθητής δεν έφθανε το κουμπί του 7ου και του 8ου ορόφου.

Οι  μαθητές που απάντησαν σωστά ήταν:
1.  Άρης Κίγκος,  Γ’ γυμνασίου
2.  Άρης Αρβανιτάκης,  Γ’ γυμνασίου
3.  Αποστόλης Λύρας,  Γ’ γυμνασίου

5. «Το χρηματικό ποσό». Βαθμός δυσκολίας 1.   Τάξεις: όλες.

Ο Γιάννης  έχει 20 ευρώ περισσότερα από τη Γεωργία. Αν στα μισά του χρήματα προσθέσει 10 ευρώ, τότε θα έχει τόσα χρήματα όσα η Γεωργία. Πόσα χρήματα έχει ο καθένας;

Λύση: Στα μισά χρήματα του Γιάννη προσθέτουμε 10 ευρώ και βρίσκουμε τα χρήματα της Γεωργίας. Στη συνέχεια, στο προηγούμενο ποσό προσθέτουμε 20 ευρώ επιπέον και βρίσκουμε τα χρήματα που έχει συνολικά ο Γιάννης. Άρα το συνολικό ποσό του Γιάννη το βρίσκουμε αν στα μισά του χρήματα προσθέσουμε 30 ευρώ. Οπότε, τα μισά χρήματα του Γιάννη είναι 30 ευρώ, κατά συνέπεια έχει συνολικά 60 ευρώ. Άρα η Γεωργία έχει 60-20=40 ευρώ.
Ο γρίφος μπορεί να λυθεί και με τη χρήση εξισώσεων από μαθητές Β’ Γυμνασίου και άνω.

Οι μαθητές που απάντησαν σωστά ήταν:
1. Άρης Κίγκος, Γ΄ γυμνασίου
2. Ιωάννα Μουτζούρη, Α΄ γυμνασίου
3. Απόστολος Λύρας, Γ΄ γυμνασίου
4. Άρης Αρβανιτάκης, Γ΄ γυμνασίου
5. Γιάννης Τζαβάρας, Α΄ γυμνασίου

6. «Ο αγώνας δρόμου ». Βαθμός δυσκολίας 2. Τάξεις: όλες.

Ο Γρηγόρης και ο Βασίλης έτρεξαν σε μια κούρσα 100 μέτρων. Όταν ο Γρηγόρης τερμάτισε, ο Βασίλης βρισκόταν στα 90 μέτρα (10 μέτρα πριν τον τερματισμό). Στη συνέχεια, ο Γρηγόρης πρότεινε στον Βασίλη να ξανατρέξουν αλλά αυτή τη φορά θα ξεκινούσε 10 μέτρα πίσω απ’ τον Βασίλη για να είναι πιο αμφίρροπο το αποτέλεσμα. Αν κρατηθούν όλες οι άλλες συνθήκες ίδιες, ποιός θα κερδίσει; (ο Γρηγόρης, ο Βασίλης ή θα τερματίσουν ταυτόχρονα;)

Λύση:

Όταν ο Γρηγόρης θα έχει τρέξει 100 μέτρα, ο Βασίλης θα έχει τρέξει 90. Άρα θα συναντηθούν 10 μέτρα πριν τον τερματισμό. Επειδή όμως ο Γρηγόρης είναι πιο γρήγορος, θα διανύσει τα τελευταία αυτά μέτρα ταχύτερα και θα τερματίσει και πάλι πρώτος.

Οι μαθητές που απάντησαν σωστά ήταν:

1. Άρης Κίγκος, Γ’ γυμνασίου
2. Γιάννης Τζαβάρας, Α’ γυμνασίου
3. Άρης Αρβανιτάκης, Γ’ γυμνασίου

7. «Δεξιά ή αριστερά;». Βαθμός δυσκολίας 1. Τάξεις: όλες.

Προς ποια κατεύθυνση νομίζετε ότι πηγαίνει το λεωφορείο που βλέπετε και γιατί; Δεξιά ή αριστερά;

Λύση: Αφού δεν φαίνεται η πόρτα για να μπεις στο λεωφορείο, αυτή θα είναι από την άλλη πλευρά του λεωφορείου, την πλευρά δηλαδή που δεν βλέπουμε, άρα το λεωφορείο πηγαίνει προς τα αριστερά.

Οι μαθητές που απάντησαν σωστά ήταν:

1. Στέφανος Σκλαβενίτης, Α’ γυμνασίου
2. Αναστασία Παναγιωτακοπούλου, Α’ γυμνασίου
3. Άρης Αρβανιτάκης, Γ’ γυμνασίου

8. «αριθμοί σε τετράγωνα». Βαθμός δυσκολίας 2. Τάξεις: όλες.

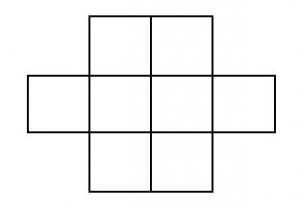
Στο παρακάτω σχήμα υπάρχου 8 μικρά και ίσα τετράγωνα. Θέλουμε να τοποθετήσουμε σ’ αυτά τους φυσικούς αριθμούς 1 έως 8, έτσι ώστε: α) σε κάθε τετραγωνάκι να βρίσκεται ένας αριθμός και β) σε τετραγωνάκια που γειτονεύουν (δηλαδή έχουν κοινή πλευρά ή κοινή κορυφή) δεν πρέπει να βρίσκονται διαδοχικοί αριθμοί (πχ το 2 και το 3). Πώς μπορεί να γίνει αυτό;

ΥΠΟΔΕΙΞΗ: Σκεφτείτε αρχικά ποιοι αριθμοί θα τοποθετηθούν στα δύο μεσαία τετραγωνάκια.

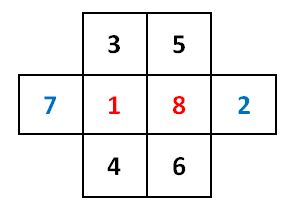
Λύση :

Οι μαθητές που απάντησαν σωστά ήταν:

1. Μάριος Ιωάννου,  Γ ’ γυμνασίου
2.Γιάννης Κοντογιώργης,  Γ’ γυμνασίου
3. Άρης Αρβανιτάκης, Γ’ γυμνασίου

4. Νάσος Τσούνης

9. «Αγώνας τένις». Βαθμός δυσκολίας 1.   Τάξεις: όλες

Δύο παιδιά παίζουν τένις. Έπαιξαν πέντε σετ και το κάθε παιδί κέρδισε τρία σετ. Πώς έγινε αυτό;

Λύση : τα δύο παιδιά δεν έπαιζαν στον ίδιο αγώνα.

Οι μαθητές που απάντησαν σωστά ήταν:

1. Λευτέρης Φουστέρης,  Α’ γυμνασίου
2.Γιώργος Ελευθερίου,  Γ’ γυμνασίου
3. Άρης Αρβανιτάκης,  Γ’ γυμνασίου

10. «Τα γάντια του σκιέρ». Βαθμός δυσκολίας 1.   Τάξεις: όλες

Ένας σκιέρ ξυπνάει τα χαράματα και ετοιμάζεται να πάει για σκι. Σ’ ένα συρτάρι έχει 4 μαύρα και 8 μπλε γάντια. Δυστυχώς το δωμάτιο είναι πολύ σκοτεινό για να διακρίνει τα χρώματά τους. Πόσα γάντια πρέπει να πάρει τουλάχιστον μαζί του για να είναι σίγουρος ότι έχει δύο του ίδιου χρώματος;

Λύση : πρέπει να πάρει 3 τουλάχιστον γάντια.

Οι μαθητές που απάντησαν σωστά ήταν:

1. Στέφανος Σκλαβενίτης,  Α’ γυμνασίου
2. Άρης Κίγκος,  Γ’ γυμνασίου
3. Κλειώ Σαιτάκη,  Α’ γυμνασίου

4. Ελένη Τασιά,  Α’ γυμνασίου

5. Γιάννης Τζαβάρας,  Α’ Γυμνασίου

11. «Χριστούγεννα – Πρωτοχρονιά». Βαθμός δυσκολίας 1.   Τάξεις: όλες

Είναι γνωστό πως ότι ημέρα πέσουν τα Χριστούγεννα την ίδια μέρα πέφτει και η Πρωτοχρονιά. Το 2000 τα Χριστούγεννα έπεσαν Δευτέρα και η Πρωτοχρονιά Σάββατο. Πώς έγινε αυτό ;

Λύση :

Ότι ημέρα πέσουν τα Χριστούγεννα την ίδια μέρα πέφτει και η Πρωτοχρονιά, όμως πρόκειται για δύο μέρες που δεν ανήκουν ημερολογιακά στο ίδιο έτος. Η Πρωτοχρονιά και  τα Χριστούγεννα  του ίδιου έτους δεν πέφτουν την ίδια μέρα. Η Πρωτοχρονιά του 2013 ήταν Τρίτη και τα Χριστούγεννα του 2013 θα είναι Τετάρτη.

Οι μαθητές που απάντησαν σωστά ήταν:

1.Ελένη Τασιά,  Α’ γυμνασίου
2. Άρης Κίγκος,  Γ’ γυμνασίου
3. Μαριάννα Χαμπέση,  Α’ γυμνασίου

12. «Ο μικρότερος αριθμός  κουτιών». Βαθμός δυσκολίας 1.   Τάξεις: όλες

Έχουμε 3 κουτιά από τα οποία το ένα περιέχει σοκολατάκια, το άλλο µπισκότα και αυτό που απομένει περιέχει καραµέλες. Κάθε κουτί έχει µια ετικέτα στην οποία αναγράφεται το περιεχόµενό του. Οι ετικέτες  όµως, έχουν µπει λάθος και στα τρία κουτιά. Ποιος είναι ο μικρότερος αριθμός  κουτιών που πρέπει να ανοίξουμε για να ßρούμε τι περιέχει κάθε κουτί; (πώς εξηγείται αυτό;)

Λύση:

Χρειάζεται  να ανοίξουμε μόνο ένα κουτί  γιατί  αν ξέρουμε το περιεχόμενο ενός κουτιού, τότε μπορούμε να πούμε με βεβαιότητα τι περιέχουν τα άλλα δύο κουτιά. Ας πούµε ότι ανοίγουμε το κουτί που η ετικέτα του γράφει “σοκολατάκια” και ßρίσκουμε  τις καραµέλες. Από αυτό καταλαβαίνουμε  ότι το κουτί µε ετικέτα “µπισκότα” θα περιέχει τα σοκολατάκια, αφού δεν µπορεί να περιέχει ούτε τα µπισκότα (λόγω της ετικέτας του) ούτε τις καραμέλες (αφού τις βρήκαμε στο προηγούμενο κουτί). Τέλος, το κουτί µε ετικέτα “καραµέλες” θα περιέχει τα µπισκότα.

Οι μαθητές που απάντησαν σωστά ήταν:

1. Άρης Αρβανιτάκης,  Γ’ γυμνασίου

2. Λουΐζα Μπέλκα,  Α’ γυμνασίου

3. Ιωάννα Μουτζούρη,  Α’ γυμνασίου

13. «Η πιο ελαφριά μπάλα». Βαθμός δυσκολίας 2.   Τάξεις: όλες

Έχουµε 9 µπάλες του ίδιου μεγέθους, άλλα µία από αυτές έχει διαφορετικό ßάρος, είναι πιο ελαφριά. Ακόµα έχουµε µία ζυγαριά και θέλουµε να ßρούµε την ελαφρύτερη µπάλα κάνοντας δύο µόνο ζυγίσεις. Πώς θα γίνει αυτό;  (Η ζυγαριά δεν είναι από αυτές που της ßάζεις ένα αντικείµενο και σου λέει το ßάρος του άλλα αυτή που έχει δύο δίσκους και συγκρίνει δυο αντικείµενα)

Λύση :

Θα επιλέξουμε αρχικά, στην τύχη,  έξι από τις εννιά μπάλες και θα ßάλουµε τρεις µπάλες στον ένα δίσκο της ζυγαριάς και άλλες τρεις στον άλλο δίσκο. Αν η ελαφρύτερη µπάλα είναι σε µία από τις δυο πλευρές, δηλαδή σε µία τριάδα, τότε κάνουμε μια δεύτερη κατά σειρά ζύγιση και  ζυγίζουμε- συγκρίνουμε τις δύο από τις τρεις µπάλες αυτής της τριάδας.  Αν ζυγίζοντας αυτές τις δύο μπάλες , διαπιστώσουμε ότι  µία από τις δυο είναι ελαφρύτερη, τότε θα έχουμε βρει αυτό που αναζητούσαμε, αλλιώς θα είναι η τρίτη η ελαφρύτερη. Αν η ζητούμενη µπάλα δεν είναι σε καµία από τις δυο τριάδες που ζυγίσαμε αρχικά, τότε θα είναι στην άλλη τριάδα, οπότε θα πάρουμε από εδώ τις δύο μπάλες και θα συνεχίσουμε όπως πριν με τη δεύτερη ζύγιση.

Απάντησε σωστά:

Λουΐζα  Μπέλκα,  Α’ Γυμνασίου.

 

14. Η πυραμίδα.  Βαθμός δυσκολίας 1.   Τάξεις: όλες

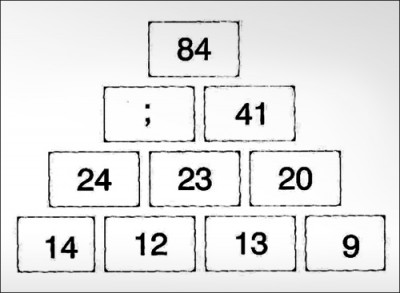
Μπορείτε να βρείτε ποιος αριθμός λείπει από την πυραμίδα;

Λύση:

Λείπει ο αριθμός 45.

Κάθε κουτί περιέχει το άθροισμα των δύο αριθμών που βρίσκονται στα ακριβώς από κάτω κουτιά μείον τον αριθμό 2.

Απάντησαν σωστά οι μαθητές:

Κώστας Χαλδαίος

Αντώνης Μπελχάτζ