Έχετε παρατηρήσει το σχήμα του κατόπτρου κατά την τελετή αφής της Ολυμπιακής φλόγας;
Αναγνωρίζετε την καμπύλη στον σχηματισμό του ουράνιου τόξου;
Μπορείτε να σχεδιάσετε την τροχιά ενός βλήματος όταν εκτοξεύεται πλάγια σε σχέση με τον ορίζοντα;
Στη φύση, η καμπύλη της παραβολής συναντάται από τις τροχιές κίνησης ως τον σχηματισμό λόφων και κοιλάδων.
Στις ανθρώπινες κατασκευές, όπως τα παραβολικά πιάτα των τηλεοράσεων, τα παραβολικά φανάρια αυτοκινήτων και μηχανών, τα παραβολικά κάτοπτρα, τα παραβολικά τηλεσκόπια, κ.α., αξιοποιείται μια πολύ σημαντική ιδιότητα της παραβολής, η ανακλαστική ιδιότητα, χάρη στην οποία διάφοροι τύποι κυμάτων, όπως φως, ήχος, ακτινοβολίες συγκεντρώνονται σ΄ένα σημείο, σε μια εστία.
Οι ακόλουθες διαδραστικές εφαρμογές αποσκοπούν στο να αναδείξουν την αξία της αλγεβρικής περιγραφής αυτής της καμπύλης.
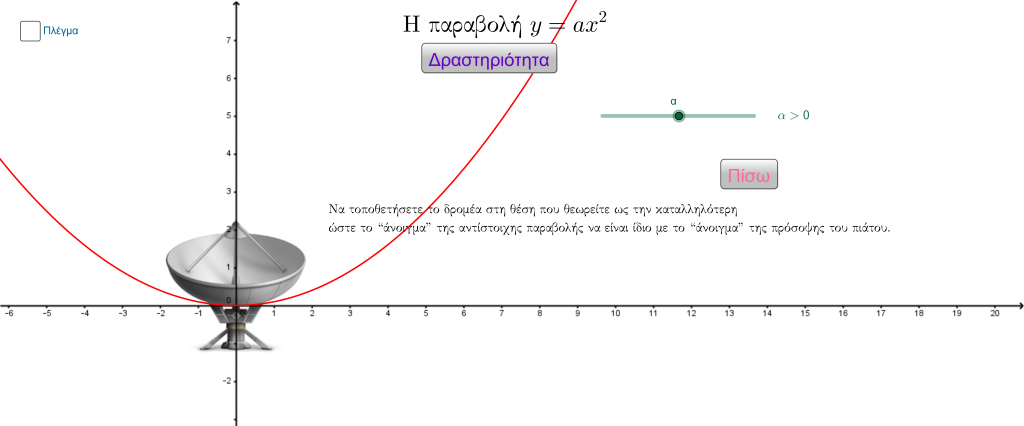
Παραβολικό πιάτο
Ο Σώτος αναλαμβάνει να διερευνήσει πως μεταβάλλεται το ύψος ενός παραβολικού πιάτου τηλεόρασης, σε σχέση με το “πλάτος” του, για λογαριασμό της εταιρείας στην οποία εργάζεται. Μπορείτε να τον βοηθήσετε;
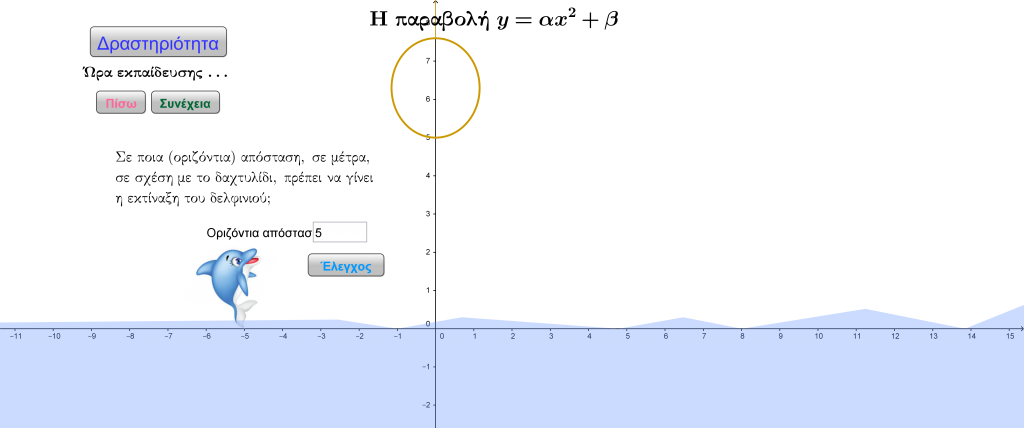
Εκπαιδεύοντας το δελφίνι
“Σώτος” είναι το όνομα ενός δελφινιού που, λόγω τραυματισμού, βρίσκεται σ΄ ένα κέντρο αποκατάστασης δελφινιών. Μπορείτε να τον βοηθήσετε να ανακτήσει τις αλτικές του ικανότητες;