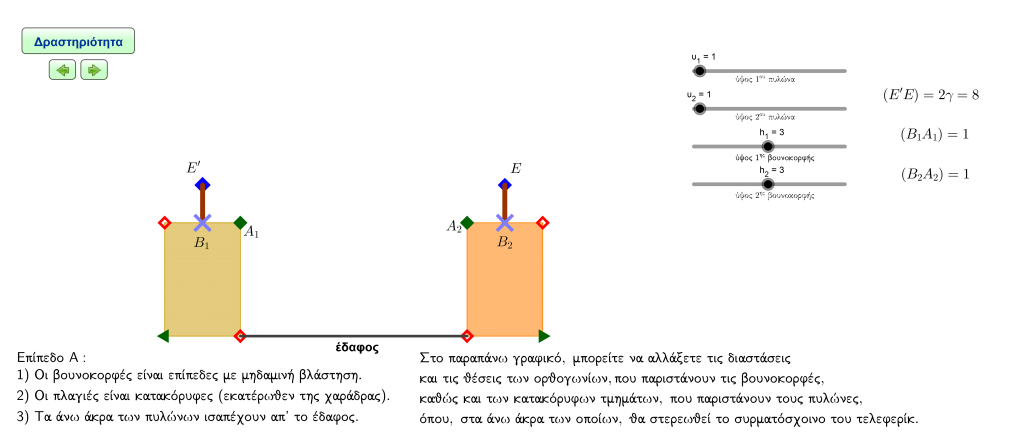
Στην παρακάτω διαδραστική εφαρμογή, ο σχεδιασμός ενός τελεφερίκ, σε τρεις διαφορετικές περιπτώσεις – επίπεδα δυσκολίας, έτσι, ώστε, να πραγματοποιείται, απρόσκοπτα, η διαδρομή του, μεταξύ δύο βουνοκορφών, φαίνεται να προϋποθέτει τη μελέτη μιας καμπύλης, ίσως, με χρήση αλγεβρικών μεθόδων. Μπορείτε να βοηθήσετε το μηχανικό που έχει αναλάβει να σχεδιάσει το έργο;
Συγγραφέας: dkonas | Κατηγορία Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 11-09-2015
Συγγραφέας: dkonas | Κατηγορία Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 20-07-2015
Μια ομάδα οικολόγων προσπαθεί να εντοπίσει ένα νεογέννητο, από ένα σπάνιο είδος φώκιας, για το οποίο έχει πληροφορηθεί ότι έχει βρει καταφύγιο σε μια σπηλιά, σε μια βραχώδη περιοχή, βόρεια ενός νησιού.
Το πλήρωμα του σκάφους, που θα αναλάβει την αποστολή, θα χρειαστεί τις μαθηματικές σας γνώσεις στα ερωτήματα που, διαδοχικά, θα κληθεί να απαντήσει.
Μπορείτε να βοηθήσετε;
Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 27-06-2015
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 30-05-2015
Μια συγκεκριμένη μέθοδος “τετραγωνισμού” της υπερβολής,
\[y=\frac{\alpha}{x}, \,\,\,\, x \neq 0\]
δηλαδή, προσέγγισης από ορθογώνια του εμβαδού του χωρίου που περικλείεται από το γράφημά της, τον οριζόντιο άξονα, και δύο κατάλληλες κατακόρυφες ευθείες, οδηγεί με φυσικό τρόπο στην έννοια της λογαριθμικής συνάρτησης με βάση τον αριθμό e.
Η μέθοδος αυτή, ίσως, να πρέπει να αποδοθεί στον Βέλγο Ιησουίτη Grégoire de Saint – Vincent (1584 – 1667), γνωστό με το προσωνύμιο του “κυκλοτετραγωνιστή”, ο οποίος σίγουρα στηρίχθηκε σε προγενέστερες εργασίες του Γάλλου μαθηματικού και δικηγόρου Pierre de Fermat (1601 – 1665) για το αντίστοιχο πρόβλημα τετραγωνισμού καμπυλών που περιγράφονται από τον γενικό τύπο,
\[
y=x^n.
\]
(Γενικευμένες Παραβολές.)
Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής μπορείτε να δοκιμάσετε να “τετραγωνίσετε” την υπερβολή, σκια … γραφώντας την αντίστοιχη λογαριθμική συνάρτηση.
Αναφορές
- Maor Eli, e: Η Ιστορία ενός αριθμού, Πανεπιστήμιο Loyola, Σικάγο, Εκδόσεις κάτοπτρο
Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Λυκείου, Για τη Β΄ Λυκείου | , στις 06-04-2015
Δύο παιδιά, με καλές γνώσεις Γεωμετρίας, κάνουν δύσκολη τη ζωή του χειριστή ενός παιχνιδιού στο Λούνα Παρκ “Μηδείς αγεωμέτρητος εισίτω” …
Μπορείτε να τον βοηθήσετε;
Αναφορές
Συγγραφέας: dkonas | Κατηγορία Μαθηματικά Θετικών Σπουδών Γ΄ Λυκείου | , στις 08-03-2015
Ισότητα
Το σύμβολο “$=$” και η σχέση που παριστάνει δε χρειάζονται ιδιαίτερες συστάσεις:
Από τις πρώτες τάξεις του Δημοτικού, το έχετε συναντήσει, αμέτρητες φορές, σε εκείνες τις περιπτώσεις που δύο μαθηματικά αντικείμενα δε διαφοροποιούνται μέσα στο εννοιολογικό πλαίσιο που ορίζονται.
Για παράδειγμα, $3+2=5,\, 90^{\circ}-45^{\circ }=45^{\circ},\, \vec{\alpha}-\vec{\alpha}=\vec{0}$ , “Δύο κύκλοι με ίσες ακτίνες είναι ίσοι” κ.ά..
Ισότητα ή Ισοδυναμία;
Από την άλλη μεριά, πόσο εύκολα, αλήθεια, ασπαστήκατε “ισότητες”, όπως,
\[$\dfrac{1}{3}=\dfrac{2}{6}=\dfrac{3}{9}=\ldots $,\]
όταν τις συναντήσατε για πρώτη φορά, κατά τη μελέτη των κλασμάτων;
Ίσως, ακόμη και τώρα, να νιώθετε άβολα μ΄ αυτήν την ταύτιση διαφορετικών, κατασκευαστικά, μαθηματικών αντικειμένων. Άλλωστε, ο αρχικός χαρακτηρισμός “ισοδύναμα κλάσματα”, που συνήθως ακολουθεί την έννοια του κλάσματος, γρήγορα, προσπεράστηκε χωρίς περαιτέρω αναφορές.
Βέβαια, ενδεχομένως, να μην αναγνωρίζετε καμιά (αλγεβρική) διαφορά μεταξύ των αριθμών $\dfrac{1}{3}$ και $\dfrac{2}{6}$ καθώς, συχνά, τους ταυτίσατε, χωρίς επιφυλάξεις, όσες φορές χρησιμοποιήθηκαν στο πλαίσιο μιας μαθηματικής διεργασίας.
Τί θα συνέβαινε, όμως, π.χ. σε μια απόπειρα να επεκτείνουμε τον ορισμό,
\[$\alpha ^{\frac{\mu }{\nu }}=\root{\nu }\of{\alpha ^{\mu }},$ $\alpha \geq 0$\]
σε περιπτώσεις όπου $\alpha<0$;
Σ΄ ένα τέτοιο εγχείρημα, ενώ, για παράδειγμα, μάλλον θα συμφωνούσατε, ξεχωριστά, με καθεμία από τις ισότητες,
\[$\left( -1\right) ^{\frac{1}{3}}=\root{3}\of{-1}=-1$\]
και
\[$\left( -1\right) ^{\frac{2}{6}}=\root{6}\of{(-1)^{2}}=1$\]
εύλογα, αντιλαμβάνεστε την “αντίφαση”:
\[$\left( -1\right) ^{\frac{1}{3}}\neq \left( -1\right) ^{\frac{2}{6}}.$\]
Ένα παρεμφερές “παράδοξο”, από το Κεφάλαιο του Ολοκληρωτικού Λογισμού, εμφανίζεται, εφαρμόζοντας παραγοντική ολοκλήρωση, στο αόριστο ολοκλήρωμα,
\[$I=\displaystyle\int \frac{1}{x}\mathrm{dx}$,\]
π.χ. στο $(0,+\infty )$, όπου προκύπτει ότι,
\[$I=\displaystyle\int \frac{1}{x}\left( x\right) ^{\prime }\mathrm{dx}=x\frac{1}{x}-\int x\left( \frac{1}{x}\right) ^{\prime }\mathrm{dx}=1-\int x\frac{-1}{x^{2}}\mathrm{dx}=1+I$\]
δηλαδή, ότι $0=1$!
Άραγε, υπάρχει κάποιο λάθος στους υπολογισμούς ή στις “ισότητες” μεταξύ των παραπάνω ολοκληρωμάτων;
Αν όχι, με ποια έννοια είναι ίσα τα παραπάνω μαθηματικά αντικείμενα; Μήπως, μέσα από από κάποιο πρίσμα, θα μπορούσε να θεωρηθεί σωστή η ισότητα $0=1$;
Να ανοίξουμε, σ΄ αυτό το σημείο, μια παρένθεση και να ανακαλέσουμε τον ορισμό του σχολικού βιβλίου για το αόριστο ολοκλήρωμα:
“Το σύνολο όλων των παραγουσών μιας συνάρτησης $f$ σ΄ ένα διάστημα $\Delta$ ονομάζεται αόριστο ολοκλήρωμα της $f$ στο $\Delta$, συμβολίζεται $\displaystyle\int f(x)\mathrm{dx}$ και διαβάζεται “ολοκλήρωμα εφ του χι ντε χι”.”
Άρα, το αόριστο ολοκλήρωμα είναι σύνολο;
Αλλά, τότε, τι έννοια έχει η ισότητα $\displaystyle\int f(x)\mathrm{dx}=F(x)+c$ όπου $F$ μια παράγουσα της $f$ στο $\Delta$, που ακολουθεί στο σχολικό βιβλίο επεξηγώντας τον προηγούμενο ορισμό;
Στην πραγματικότητα, εδώ το “$=$” σημαίνει ότι οι δύο συναρτήσεις έχουν την ίδια “δυναμική” κατά την αντιπαραγώγιση, δηλαδή, αν παραγωγιστούν, τότε προκύπτει ίδιο αποτέλεσμα, ίδια συνάρτηση.
Εξακολουθείτε να πιστεύετε το ίδιο σθεναρά ότι η “ισότητα” $0=1$, του παραπάνω παραδείγματος, είναι λανθασμένη;
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 23-02-2015
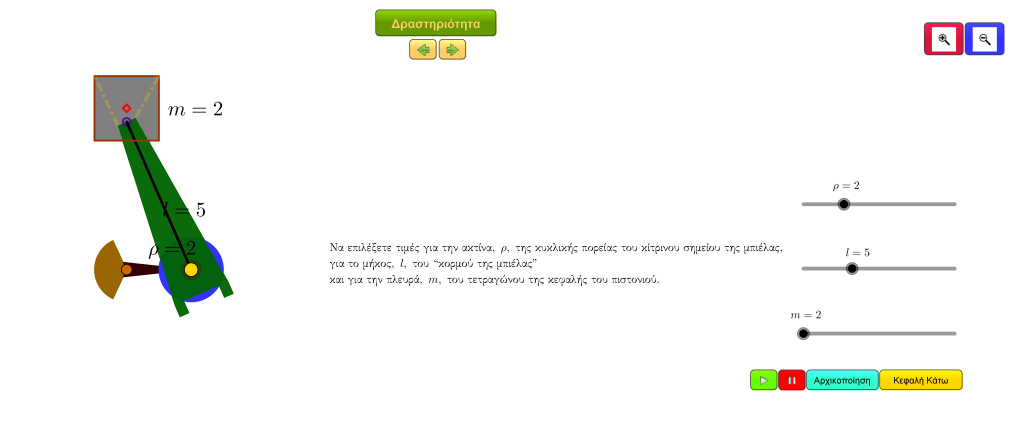
Θα έχετε, ίσως, αντιληφθεί ότι οι τριγωνομετρικές συναρτήσεις περιγράφουν, ικανοποιητικά, φαινόμενα και καταστάσεις της καθημερινής ζωής όπου το κύριο χαρακτηριστικό είναι η επανάληψη, η περιοδικότητα. Μάλλον, αυτό είναι αναμενόμενο όταν κανείς αναλογιστεί ότι στον πυρήνα του ορισμού των τριγωνομετρικών αριθμών γωνιών βρίσκεται ο κύκλος, με τον τριγωνομετρικό του “μανδύα”, το σχήμα που ενσωματώνει, ιδανικά, την έννοια της περιοδικότητας, σε συνδυασμό με την κυκλική κίνηση που προκαλείται από τις διαδοχικές θέσεις της τελικής πλευράς που μπορεί να έχει μια επίκεντρη γωνία, καθώς το μέτρο της μεταβάλλεται.
Τα προηγούμενα έρχονται στο προσκήνιο, στο αλληλεπιδραστικό περιβάλλον της ακόλουθης εφαρμογής, όταν ένας μηχανουργός προσπαθεί να περιγράψει την κίνηση για τα διάφορα μέρη ενός πιστονιού. Η εφαρμογή, αρχικά, θέτει ορισμένα απλά ερωτήματα τα οποία, σταδιακά, εισάγουν τις τριγωνομετρικές έννοιες ενώ, στην προσπάθεια να ολοκληρωθούν οι υπολογισμοί του μηχανουργού, ενδεχομένως, να διαπιστωθεί η σύνδεση της κατακόρυφης μετατόπισης ενός σημείου, που εκτελεί ομαλή κυκλική κίνηση, με την ημιτονοειδή συνάρτηση, καθώς και οι ακρότατες τιμές αυτών των μετατοπίσεων, $\rho$ και $-\rho$, όπως και ο χρόνος, $T$, που απαιτείται για μια πλήρη περιστροφή (περίοδος), με τον αντίστοιχο τύπο που αναπαριστά αυτή τη συνάρτηση. Έπειτα, η εφαρμογή περιγράφει ένα πρόβλημα που απαιτεί τη σύνθεση διάφορων τριγωνομετρικών συναρτήσεων και προϋποθέτει μια σχετική ικανότητα συνδυασμού γνώσεων, ενώ, τέλος, ελέγχει τους αλγεβρικούς χειρισμούς, κατά την επίλυση τριγωνομετρικών εξισώσεων, καλύπτοντας, έτσι, ένα σημαντικό φάσμα τριγωνομετρικών εννοιών.