Ένας ήσυχος περίπατος, δύο μαθητών, εξελίσσεται σε εφιάλτη όταν τα δύο σκυλάκια, που έχουν μαζί τους, ετοιμάζονται να διεκδικήσουν ένα κόκκαλο, που βρέθηκε στο δρόμο τους.
Θα καταφέρουν, τα δύο παιδιά, να χειριστούν, σε διάφορες περιπτώσεις, τα δύο σκυλάκια ή το εγχείρημα θα αποδειχτεί ένα δυσεπίλυτο γεωμετρικό πρόβλημα;
Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Α΄ Λυκείου, Για την Α΄ Λυκείου | , στις 18-12-2016
Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 17-12-2016
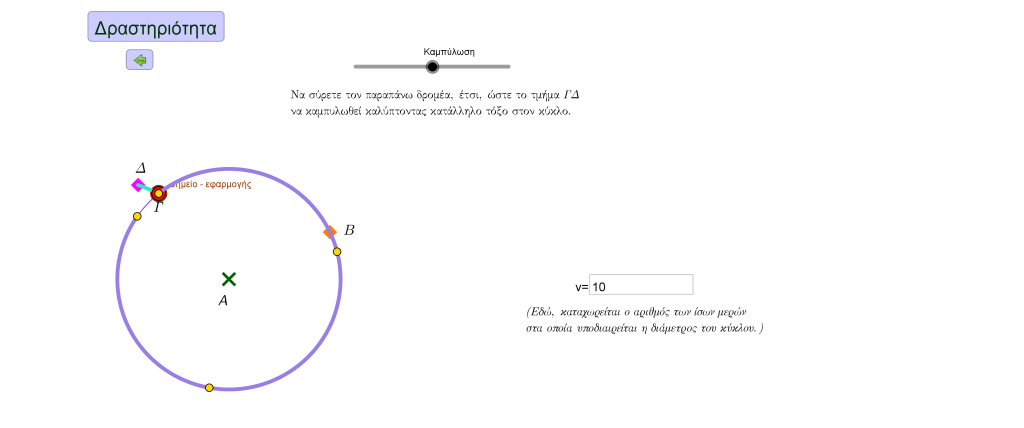
Στο πλαίσιο της ακόλουθης διαδραστικής εφαρμογής, θα κληθείτε να προσαρτήσετε τη διάμετρο ενός κύκλου στην περιφέρειά του, προσομοιώνοντας την καμπύλωσή της, ξεκινώντας από κάποιο σημείο εφαρμογής, πάνω στον κύκλο, και συνεχίζοντας, διαδοχικά, με όμοιο τρόπο, από το σημείο στο οποίο, κάθε φορά, καταλήγει, παρατηρώντας τον ακριβή αριθμό που φανερώνει πόσες φορές το καμπυλωμένο τμήμα της διαμέτρου “χωράει” στον κύκλο.
Συνεπώς, προκύπτει μια πρώτη εκτίμηση για το μήκος του κύκλου με μονάδα μέτρησης τη διάμετρό του. Πώς, όμως, θα μπορούσε η εκτίμηση αυτή να γίνει καλύτερη;
Προφανώς, η προηγούμενη διαδικασία θα μπορούσε να επαναληφθεί με χρήση κατάλληλων, κάθε φορά, υποδιαιρέσεων της διαμέτρου, ωσότου προσεγγιστεί, όσο το δυνατόν περισσότερο, το αρχικό σημείο εφαρμογής της διαμέτρου στον κύκλο, κατά το ξεκίνημα της διαδικασίας.
Η εκτίμηση θα μπορούσε να βελτιωθεί, εξαντλητικά, ανακαλύπτοντας, ολοένα και περισσότερο, τα ψηφία του αριθμού που συσχετίζουν το μήκος ενός κύκλου με τη διάμετρό του.
Έτσι, με τη βοήθειά της, μπορείτε να συνδέσετε τον αριθμό π με το “π – εριτύλιγμα …” του κύκλου από διαμέτρους και από τις υποδιαιρέσεις τους.
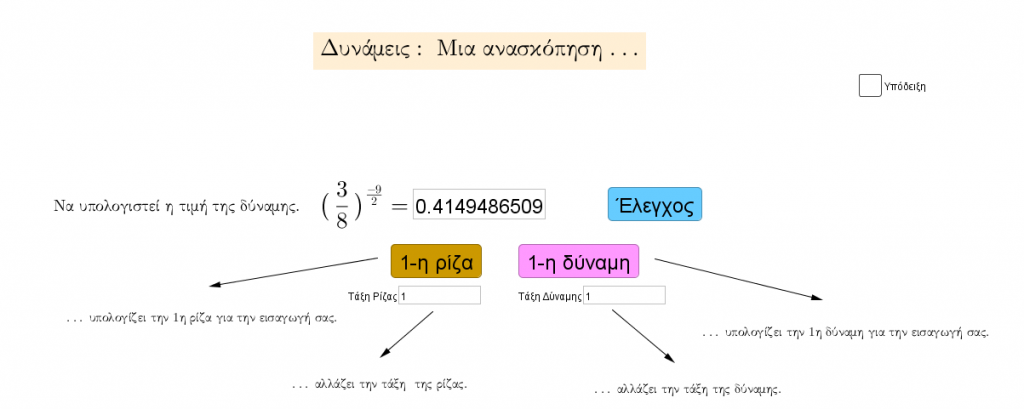
Συγγραφέας: dkonas | Κατηγορία Άλγεβρα Β΄ Λυκείου, Για τη Β΄ Λυκείου | , στις 04-12-2016
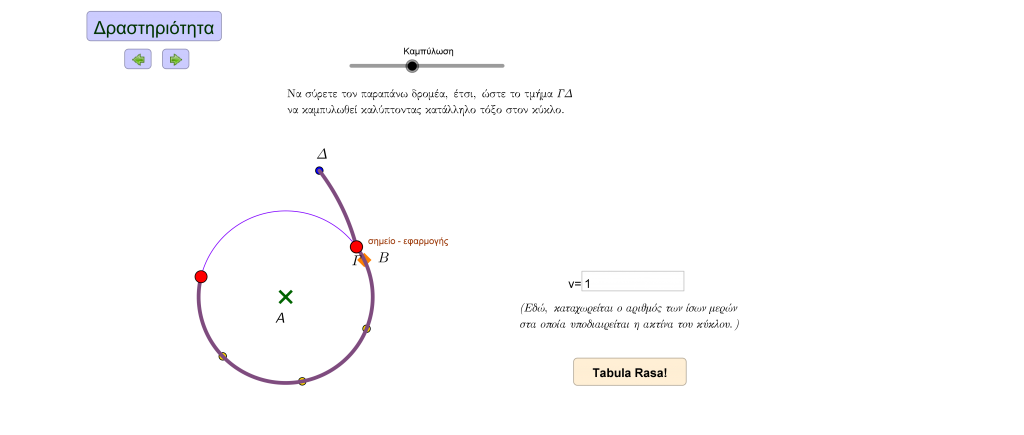
Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, μπορείτε να επιχειρήσετε να προσαρτήσετε, διαδοχικά και χωρίς αλληλεπικαλύψεις, κατάλληλο αριθμό (ακέραιων) ακτίνων ενός κύκλου στην περιφέρειά του, καμπυλώνοντας τα αντίστοιχα ευθύγραμμα τμήματά τους. Θα παρατηρήσετε ότι κάποιο μέρος του κύκλου παραμένει “ακάλυπτο”. Έτσι, μπορείτε να συνεχίσετε, παρόμοια, υποδιαιρώντας τις ακτίνες, αφού τις διαιρέσετε σε κατάλληλο αριθμό ίσων τμημάτων, για να “καλύψετε” περαιτέρω τον κύκλο. Μπορείτε να σταματήσετε όταν θεωρήσετε ότι καλύψατε, επαρκώς, τον κύκλο.
Ποιος αριθμός “μετράει” τον κύκλο, με τη βοήθεια της ακτίνας του, με βάση την κάλυψή σας;
Η διαδικασία, που περιγράφηκε παραπάνω, θα περατωθεί ποτέ;
Τελικά, τι είδους αριθμός εκφράζει τον κύκλο σε ακτίνια και ποια είναι η τιμή του;
Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Γυμνασίου, Για τη Β΄ Γυμνασίου | , στις 25-07-2016
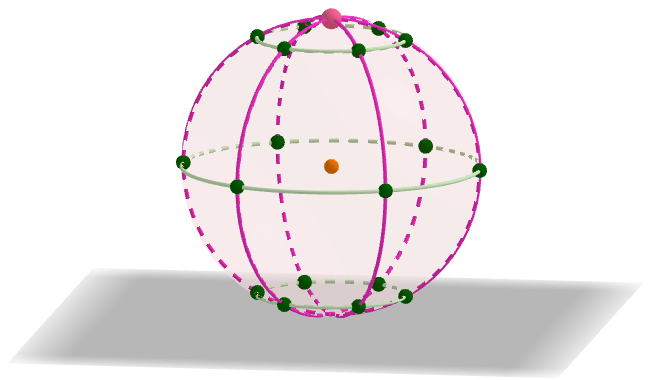
Με τη βοήθεια της ακόλουθης διαδραστικής εφαρμογής, μπορείτε να ανακαλύψετε τον τύπο που υπολογίζει το εμβαδό της επιφάνειας της σφαίρας.
Σκοπός της εφαρμογής είναι να προσομοιωθεί κατάλληλη κάλυψη της επιφάνειας της σφαίρας, η οποία δημιουργείται με τη βοήθεια “κουκκίδων” που ορίζονται από την τομή “παράλληλων” κύκλων και “μεσημβρινών” πάνω στην επιφάνειά της. Οι κουκκίδες περιστρέφονται γύρω από το “νότιο πόλο” της σφαίρας ωσότου προσεγγίσουν το “επίπεδο στήριξης” της σφαίρας, συνθέτοντας, έτσι, έναν κυκλικό δίσκο. Μπορείτε να βρείτε την ακτίνα του και το εμβαδόν του;
Συγγραφέας: dkonas | Κατηγορία Γεωμετρία Β΄ Λυκείου, Για τη Β΄ Λυκείου, Μαθηματικά Θετικών Σπουδών Β΄ Λυκείου | , στις 06-07-2016
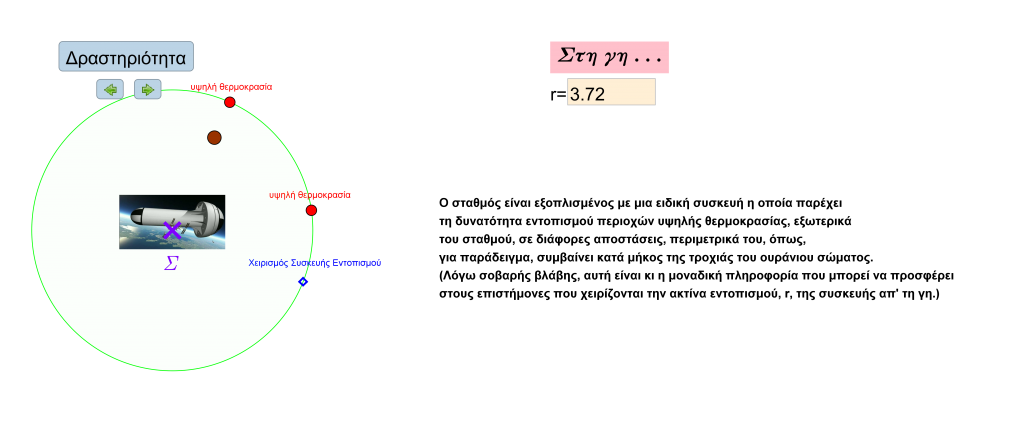
Μια ομάδα επιστημόνων, στη γη, προσπαθεί να χειριστεί δύο ειδικά διαστημικά οχήματα, ενός διαστημικού σταθμού, με σκοπό να πλησιάσει, όσο το δυνατόν περισσότερο, την κυκλική τροχιά ενός ουράνιου σώματος.
Όμως, μια απροσδόκητη βλάβη στα ηλεκτρονικά συστήματα του σταθμού, καθιστά αναγκαία την επίλυση ενός προβλήματος μετρικών σχέσεων. Μπορείτε να βοηθήσετε;