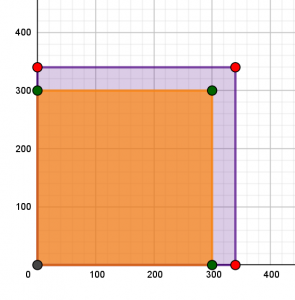
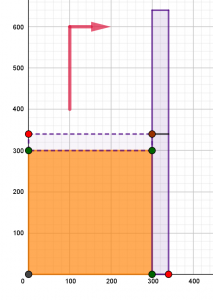
Η γενίκευση της έννοιας της γωνίας, όπως και των αντίστοιχων τριγωνομετρικών αριθμών της, αναδεικνύεται με τη βοήθεια του τριγωνομετρικού κύκλου. Ο τριγωνομετρικός κύκλος, ένας μοναδιαίος κύκλος με κέντρο την αρχή 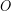 ενός ορθοκανονικού συστήματος συντεταγμένων
ενός ορθοκανονικού συστήματος συντεταγμένων  , μπορεί να δεχθεί, ως επίκεντρη, μια οποιαδήποτε γωνία,
, μπορεί να δεχθεί, ως επίκεντρη, μια οποιαδήποτε γωνία,  , η οποία, μάλιστα, τοποθετείται έχοντας ως αρχική πλευρά της τον ημιάξονα
, η οποία, μάλιστα, τοποθετείται έχοντας ως αρχική πλευρά της τον ημιάξονα  . Αν συμβολίσουμε με
. Αν συμβολίσουμε με  το σημείο στο οποίο η τελική πλευρά τέμνει τον κύκλο, τότε,
το σημείο στο οποίο η τελική πλευρά τέμνει τον κύκλο, τότε,
![Rendered by QuickLaTeX.com \[ \mathrm{cos}(\omega)=x,\,\, \mathrm{ sin}(\omega)=y,\,\, \mathrm{ tan}(\omega)=\frac{y}{x},\,\, \mathrm{ ctg}(\omega)=\frac{x}{y}. \]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-819637aae64f79e18a4bc145d8b3e376_l3.png?x32006)
Παρεμπιπτόντως, το πρόσημο της γωνίας καθορίζει τη φορά κίνησης της τελικής πλευράς, με το θετικό να αντιστοιχεί στην αριστερόστροφη, ωσότου επιτευχθεί το αντίστοιχο “άνοιγμα”.
Γνωστές σχέσεις μεταξύ γωνιών (αντίθετες γωνίες, παραπληρωματικές γωνίες, συμπληρωματικές γωνίες, γωνίες που διαφέρουν κατά  , γωνίες που διαφέρουν κατά
, γωνίες που διαφέρουν κατά 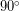 , κ.ά.) μπορούν να παρασταθούν στον τριγωνομετρικό κύκλο, ο οποίος προσφέρεται για τη διερεύνηση των αντίστοιχων σχέσεων μεταξύ των τριγωνομετρικών αριθμών αυτών των γωνιών και τελικά στην αναγωγή τους στο πρώτο τεταρτημόριο.
, κ.ά.) μπορούν να παρασταθούν στον τριγωνομετρικό κύκλο, ο οποίος προσφέρεται για τη διερεύνηση των αντίστοιχων σχέσεων μεταξύ των τριγωνομετρικών αριθμών αυτών των γωνιών και τελικά στην αναγωγή τους στο πρώτο τεταρτημόριο.
Τα προηγούμενα μπορούν να γίνουν περισσότερο κατανοητά μέσω της διαδραστικής εφαρμογής που ακολουθεί.


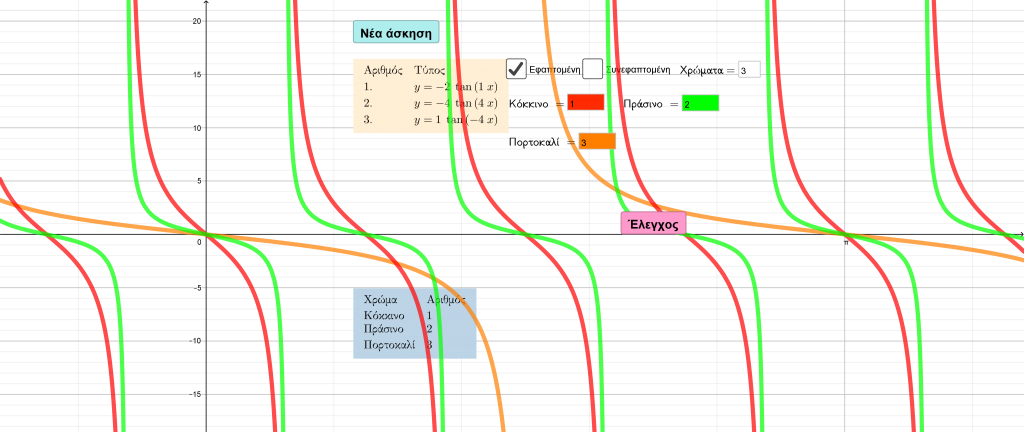
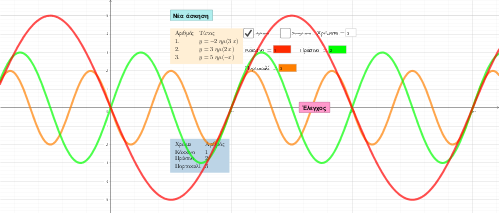

![Rendered by QuickLaTeX.com \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ {...............} \\ {} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-1a7ffe9e2200bf98eb9881628b2006c7_l3.png?x32006)
![Rendered by QuickLaTeX.com \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ {...............} \\ {} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-8e1abbcb6ed68512097b5ff2b25da723_l3.png?x32006)
![Rendered by QuickLaTeX.com \[ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \end{array}} \right|\begin{array}{*{20}{c}} {\underline{{3\text{ }...........\ }}} \\ 6 \\ {} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-8cd127dd3105d83881eaf211c202b50f_l3.png?x32006)
![Rendered by QuickLaTeX.com \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{3\text{ }...........\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-055de137987179f46ea2e43bb2e8b7b4_l3.png?x32006)
![Rendered by QuickLaTeX.com \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {90} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {90} & {} & {} \\ {} & {} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-0b5a7fe37731d611e449955c7b69eb75_l3.png?x32006)
![Rendered by QuickLaTeX.com \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {25} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \\ {} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-121bb8639ecec45fffd791e10988d749_l3.png?x32006)
![Rendered by QuickLaTeX.com \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} \\ {} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-a8526f5fe7424eb1a72dfefd5758c063_l3.png?x32006)
![Rendered by QuickLaTeX.com \[$\displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{34\text{ }.......\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-95b52c877cc5f9f79c78dce78efb205d_l3.png?x32006)
![Rendered by QuickLaTeX.com \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{345\text{ }..\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-f4f82304593e497954d3b8f338eba66b_l3.png?x32006)
![Rendered by QuickLaTeX.com \[$ \displaystyle \left. {\begin{array}{*{20}{r}} {\begin{array}{*{20}{c}} {} & {11} \end{array}} & {\begin{array}{*{20}{c}} {} & {90} \end{array}} & {\begin{array}{*{20}{c}} {} & {25} \end{array}} & {} \\ {\underline{{\begin{array}{*{20}{c}} - & 9 \end{array}}}} & {\begin{array}{*{20}{c}} {} & {} \end{array}} & {} & {} \\ {\begin{array}{*{20}{c}} {} & 2 \end{array}} & {\begin{array}{*{20}{c}} {} & {290} \end{array}} & {} & {} \\ {} & {\underline{{\begin{array}{*{20}{c}} - & {256} \end{array}}}} & {} & {} \\ {} & {\begin{array}{*{20}{c}} {} & {34} \end{array}} & {\begin{array}{*{20}{c}} {} & {3425} \end{array}} & {} \\ {} & {} & {\underline{{\begin{array}{*{20}{c}} - & {3425} \end{array}}}} & {} \\ {} & {} & {\begin{array}{*{20}{c}} {} & 0 \end{array}} & {} \end{array}} \right|\begin{array}{*{20}{r}} {\underline{{\text{ }345\text{ }\ }}} & {} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}64} & {\begin{array}{*{20}{c}} {} & {} \end{array}685} \\ {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}4}}} & {\underline{{\begin{array}{*{20}{c}} \times & {} \end{array}5}}} \\ {\begin{array}{*{20}{c}} {} & {} \end{array}256} & {\begin{array}{*{20}{c}} {} & {} \end{array}3425} \\ {} & {} \\ {} & {} \\ {} & {} \end{array}$\]](https://blogs.sch.gr/dkonas/wp-content/ql-cache/quicklatex.com-814a14f43b87dc0715adb83f5dd7f645_l3.png?x32006)