Η γενική μορφή εξίσωσης δεύτερου βαθμού στο επίπεδο, δηλαδή μια εξίσωση της μορφής,
(1) 
μπορεί να αποδειχτεί ότι, στην περίπτωση που δεν είναι αδύνατη, παριστάνει είτε ζεύγος παράλληλων ευθειών είτε μια κωνική τομή: έλλειψη – κύκλος – σημείο, παραβολή, υπερβολή – ζεύγος τεμνόμενων ευθειών.
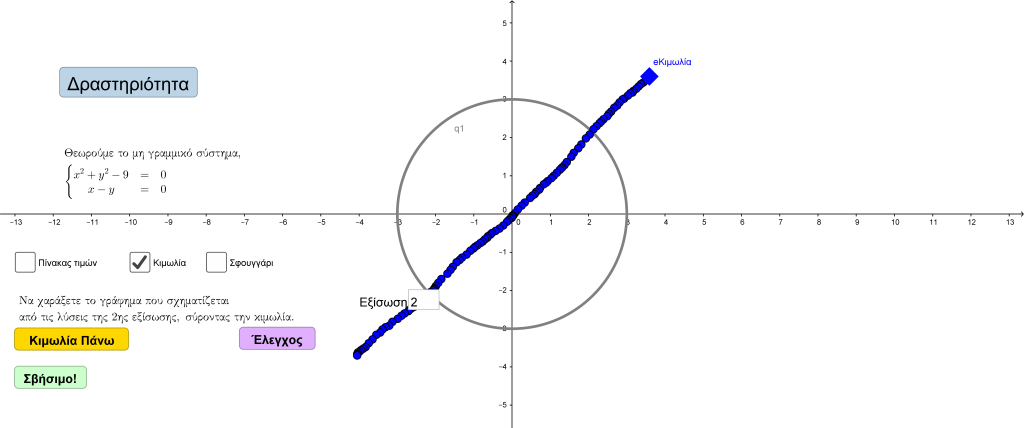
Η παρακάτω διαδραστική εφαρμογή παρέχει τη δυνατότητα σχεδίασης και ελέγχου του γραφήματος κάθε εξίσωσης, ενός συστήματος δύο τέτοιων εξισώσεων, οπότε, τελικά, της γραφικής του επίλυσης.
Copyright © 2017. Με την επιφύλαξη όλων των δικαιωμάτων.